Notes
Article history
This issue of the Health Technology Assessment journal series contains a project commissioned by the MRC–NIHR Methodology Research Programme (MRP). MRP aims to improve efficiency, quality and impact across the entire spectrum of biomedical and health-related research. In addition to the MRC and NIHR funding partners, MRP takes into account the needs of other stakeholders including the devolved administrations, industry R&D, and regulatory/advisory agencies and other public bodies. MRP supports investigator-led methodology research from across the UK that maximises benefits for researchers, patients and the general population – improving the methods available to ensure health research, decisions and policy are built on the best possible evidence.
To improve availability and uptake of methodological innovation, MRC and NIHR jointly supported a series of workshops to develop guidance in specified areas of methodological controversy or uncertainty (Methodology State-of-the-Art Workshop Programme). Workshops were commissioned by open calls for applications led by UK-based researchers. Workshop outputs are incorporated into this report, and MRC and NIHR endorse the methodological recommendations as state-of-the-art guidance at time of publication.
The authors have been wholly responsible for all data collection, analysis and interpretation, and for writing up their work. The HTA editors and publisher have tried to ensure the accuracy of the authors’ report and would like to thank the reviewers for their constructive comments on the draft document. However, they do not accept liability for damages or losses arising from material published in this report.
Declared competing interests of authors
Lisa V Hampson is an employee of Novartis Pharma AG (Basel, Switzerland) and reports grants from the Medical Research Council (MRC). Catherine Hewitt is a member of the National Institute for Health Research (NIHR) Health Technology Assessment (HTA) Commissioning Board since 2015. Jesse A Berlin is an employee of Johnson & Johnson (New Brunswick, NJ, USA) and holds shares in this company. Richard Emsley is a member of the NIHR HTA Clinical Trials Board since 2018. Deborah Ashby is a member of the HTA Commissioning Board, HTA Funding Boards Policy Group, HTA Mental Psychological and Occupational Health Methods Group, HTA Prioritisation Group and the HTA Remit and Competitiveness Group from January 2016 to December 2018. Stephen J Walters declares his department has contracts and/or research grants with the Department of Health and Social Care, NIHR, MRC and the National Institute for Health and Care Excellence. He also declares book royalties from John Wiley & Sons, Inc. (Hoboken, NJ, USA), as well as a grant from the MRC and personal fees for external examining. Louise Brown is a member of the NIHR Efficacy and Mechanism Evaluation Board since 2014. Craig R Ramsay is a member of the NIHR HTA General Board since 2017. Andrew Cook is a member of the NIHR HTA Interventional Procedures Methods Group, HTA Intellectual Property Panel, HTA Prioritisation Group, Public Health Research (PHR) Research Funding Board, Public Health Research Prioritisation Group and the PHR Programme Advisory Board.
Permissions
Copyright statement
© Queen’s Printer and Controller of HMSO 2019. This work was produced by Cook et al. under the terms of a commissioning contract issued by the Secretary of State for Health and Social Care. This issue may be freely reproduced for the purposes of private research and study and extracts (or indeed, the full report) may be included in professional journals provided that suitable acknowledgement is made and the reproduction is not associated with any form of advertising. Applications for commercial reproduction should be addressed to: NIHR Journals Library, National Institute for Health Research, Evaluation, Trials and Studies Coordinating Centre, Alpha House, University of Southampton Science Park, Southampton SO16 7NS, UK.
2019 Queen’s Printer and Controller of HMSO
Chapter 1 Introduction
Synopsis
The aim of this document is to provide practical help on the choice of target difference used in the sample size calculation of a randomised controlled trial (RCT). Advice is provided with a definitive trial, that is, one that seeks to provide a useful answer, in mind and not those of a more exploratory nature. The term ‘target difference’ is taken throughout to refer to the difference that is used in the sample size calculation (the one that the study formally ‘targets’). Please see the Glossary for definitions and clarification with regard to other relevant concepts. To address the specification of the target difference, it is appropriate, and to some degree necessary, to touch on related statistical aspects of conducting a sample size calculation. Generally, the discussion of other aspects and more technical details is kept to a minimum, with more technical aspects covered in the appendices and referencing of relevant sources provided for further reading.
The main body of this report assumes a standard RCT design is used; formally, this can be described as a two-arm parallel-group trial. Most RCTs test for superiority of the interventions, that is whether or not one of the interventions is superior to the other (Box 1 provides a formal definition of superiority and of the two most common alternative approaches). A rationale for the report is provided in Rationale for this report and a summary of the research stages that were used to inform this report is provided in Development of the DELTA2 advice and recommendations. Appendices 1 and 2 provide fuller details, which have also been published elsewhere. 9 The conventional approach to sample size calculations is discussed along with other relevant topics in Appendix 3. Additionally, it is assumed in the main body of the text that the conventional (Neyman–Pearson) approach to the sample size calculation of a RCT is being used. Other approaches (Bayesian, precision and value of information) are briefly considered in Appendix 4, with reference to the specification of the target difference. Some of the more common alternative trial designs to a two-arm parallel-group superiority trial are considered in Appendix 5.
In a superiority trial with a continuous primary outcome, the objective is to determine whether or not there is evidence of a difference in the desired outcome between intervention A and intervention B, with mean response µA and µB, respectively. 1 The null (H0) and alternative (H1) hypotheses typically under consideration are:
H0, the means of the two intervention groups are not different (i.e. µA = µB).
H1, the means of the two intervention groups are different (i.e. µA ≠ µB).
For a superiority trial, the null hypothesis can be rejected if µA > µB or if µA < µB based on a statistically significant test result. 1,2 This leads to the possibility of making a type I error when the null hypothesis is true (i.e. there is no difference between the interventions). The statistical test is referred to as a two-tailed test, with each tail allocated an equal amount of the type I error (α/2, typically set at 2.5%). The null hypothesis can be rejected if the test of µA < µB is statistically significant at the 2.5% level or the test of µA > µB is statistically significant at the 2.5% level. The sample size is calculated on the basis of applying such a statistical test, given the magnitude of a difference that is desired to be detected (the target difference), and the desired type I error rate and statistical power. Consideration of a difference in only one direction (one-sided test) is also possible.
Equivalence trialThe objective of an equivalence trial is not to demonstrate the superiority of one treatment over another, but to show that two interventions have no clinically meaningful difference, that is they are clinically equivalent (or not different). 3 The corresponding hypotheses for an equivalence trial (continuous primary outcome) take the following form.
H0, there is a difference between the means of the two groups (i.e. they are not ‘equivalent’):
or
H1: there is a no difference between the means of the two groups (i.e. they are ‘equivalent’):
where dE equates to the largest difference that would be acceptable while still being able to conclude that there is no difference between interventions. It is often called the equivalence margin. µA and µB are defined as before.
To conclude equivalence, both components of the null hypothesis need to be rejected. One approach to performing an equivalence trial is to test both components, which is called the TOST procedure. 1,3 This can be operationally the same as constructing a (1 – α)100% CI and concluding equivalence if the CI falls completely within the interval (–dE, dE). For example, dE could be set to 10 (on the scale of interest). After conducting the trial, a 95% CI for the difference between interventions could be (–3 to 7). As the CI is wholly contained within (–10 to 10), the two interventions can be considered to be equivalent.
Non-inferiority trialA non-inferiority trial can be considered a special case of an equivalence trial. The objective is to demonstrate that a new treatment is not clinically inferior to an established one. This can be formally stated under null (H0) and alternative (H1) hypotheses for a non-inferiority trial (continuous primary outcome) that take the form:
H0, treatment A is inferior to B in terms of the mean response µB – µA > dNI,
H1, treatment A is non-inferior to B in terms of the mean response µB – µA ≤ dNI,
where dNI is defined as the difference that is clinically acceptable for us to conclude that there is no difference between interventions, and a higher score on the outcome is a better outcome. Non-inferiority trials reduce to a simple one-sided hypothesis and test, and correspondingly are usually operationalised by constructing a one-sided (1 – α/2)100% CI. Non-inferiority can be concluded if the upper end of this CI is not greater than dNI. No restriction is made regarding whether the new intervention is the same as or better than the other intervention. A mean difference far from dNI, in the positive direction, is not a negative finding, whereas for an equivalence trial it could rule out equivalence.
Equivalence and non-inferiority marginsThe setting of an equivalence (and non-inferiority) margin, or limit, is a controversial topic. There are regulatory guidelines on the topic, although practice has varied. 4,5 It has been defined more tightly, and arguably appropriately, as the ‘largest difference that is clinically acceptable, so that a difference bigger than this would matter in practice’. 6 A natural approach would be for dE to be just smaller than the MCID (see Chapter 3, Methods for specifying the target difference). In the context of replacement pharmaceuticals, the margin has been suggested to ‘[be no] greater than the smallest effect size that the active (control) drug would be reliably expected to have when compared with placebo in the setting of the planned trial’. 7 An acceptable margin can therefore be chosen via a retrospective comparison with placebo that shows that the new treatment is non-inferior to the standard treatment, and thereby indirectly shows that the new treatment is superior to placebo. 8 It may also be desirable to demonstrate no substantive non-inferiority, leading to a narrower margin, similar to the approach above.
CI, confidence interval; MCID, minimum clinically important difference; TOST, two one-sided test.
Rationale for this report
A RCT is widely considered to be the optimal study design to assess the comparative clinical efficacy and effectiveness along with the cost implications of health interventions. 1 RCTs are routinely used to assess the use of new drugs prior to, and in order to secure, approval for releasing new drugs to market. More generally, they have also been widely used to evaluate a range of interventions and have been successfully used in a variety of health-care settings. An a priori sample size calculation ensures that the study has a reasonable chance of achieving its prespecified objectives. 10
A number of statistical approaches exist for calculating the required sample size. 1,11,12 However, a recent review of 215 RCTs in leading medical journals identified only the conventional (Neyman–Pearson) approach in use. 13 This approach requires establishment of the statistical significance level (type I error rate) and power (1 minus the type II error rate), alongside the target difference (‘effect size’). Setting the statistical significance level and power represents a compromise between the possibility of being misled by chance, when there is no true difference between the interventions, and the risk of not identifying a difference, when one of the interventions is truly superior, whereas the target difference is the magnitude of difference to be detected between sample sets. The required sample size is very sensitive to the target difference. Halving it roughly quadruples the sample size for the standard RCT design. 1
A comprehensive review conducted by the original Difference ELicitation in TriAls (DELTA) group14,15 highlighted the available methods for specifying the target difference. Despite there being many different approaches available, few appear to be in regular use. 16 Much of the work on identifying important differences has been carried out on patient-reported outcomes, specifically those seeking to measure health-related quality of life. 17,18 In practice, the target difference often appears not to be formally based on these concepts and in many cases appears, at least from trial reports, to be determined based on convenience or some other informal basis. 19 Recent surveys among researchers involved in clinical trials demonstrated that the practice is more sophisticated than trial reports suggest. 16 The original DELTA group developed initial advice, but this was restricted to a standard superiority two-arm parallel-group trial design and limited consideration of related issues. 20 It did not provide recommendations for practice. Accordingly, there is a gap in the literature to address this and thereby help improve current practice, which this report seeks to address. The Medical Research Council (MRC)/National Institute for Health Research (NIHR) Methodology Research Panel in the UK commissioned a workshop to produce advice on this choice of ‘effect size’ in RCT sample size calculations. From this resulting DELTA project, this report was produced. The process of its development is described in Development of the DELTA2 advice and recommendations.
Development of the DELTA2 advice and recommendations
The DELTA2 project had five components: systematic literature review of recent methodological developments (stage 1); literature review of existing funder advice (stage 2); a Delphi study (stage 3); a 2-day consensus meeting bringing together researchers, funders and patient representatives (stage 4); and the preparation and dissemination of an advice and recommendations document (stage 5). Full details of the methods and findings are provided in Appendices 1 and 2 and are summarised here.
The project started in April 2016. A search for relevant documentation on the websites of 15 trial-funding advisory bodies was performed (see Appendix 1, Methodology of the literature reviews, Delphi study, consensus meeting, stakeholder engagement and finalisation of advice and recommendations). However, there was little specific advice provided to assist researchers in specifying the target difference. The literature search for methodological developments identified 28 articles of methodological developments relevant to a method for specifying a target difference. A Delphi study involving two stages and 69 participants was conducted. The first round focused mainly on topics of interest and was conducted between 11 August 2016 and 10 October 2016. In the second round, which took place between 1 September 2017 and 12 November 2017, participants were provided with a draft copy of the document and feedback was invited.
The 2-day workshop was held in Oxford on 27 and 28 September 2016, and involved 25 participants, including clinical trials unit (CTU) directors, study investigators, project funder representatives, funding panel members, researchers, experts in sample size methods, senior trial statisticians and patient and public involvement (PPI) representatives. At this workshop, the structure and general content of the document was agreed; it was subsequently drafted by members of the project team and participants from the workshop. Further engagement sessions were held at the Society for Clinical Trials (SCT), Statisticians in the Pharmaceutical Industry (PSI) and Joint Statistical Meetings (JSM) conferences on 16 May 2016, 17 May 2017 and 1 August 2017, respectively. The main text was finalised on 18 April 2018, after revision informed by feedback gathered from the second round of the Delphi study, the aforementioned engagement sessions and from funder representatives. Minor revisions in the light of editorial and referee feedback were made prior to finalising this report.
Chapter 2 General considerations for specifying the target difference
Target differences and the analysis of interest
Randomised controlled trial design begins with clarifying the research question and then developing the required design to address it. Commonly the population, intervention, control, outcome and time frame (PICOT) framework has been used for this purpose. 21 All of the relevant aspects of trial design (PICOT) should reflect the research questions of interest. The process of determining the design needs to be informed by the perspective(s) of relevant stakeholders, which are discussed in the following section (see Perspectives on the target difference of interest). A key step in the process is the selection of the primary outcome, which is considered in The primary outcome of a randomised controlled trial, given its key role in trial design and its relationship with the target difference. This section focuses on the need for clarity about how the design and intended analysis address the trial objectives.
The need for greater clarity in trial objectives with respect to the design and analysis of a RCT has been noted. 22 This reflects greater recognition of the existence of multiple intervention (or treatment) effects of potential interest, even for the same outcome. For example, we may be interested in the typical benefit a patient received if they are given a treatment, but also the benefit a patient receives if they comply fully with the treatment (e.g. they take their medication as prescribed for the full treatment period, with use of additional treatments). Treatment effects can differ subtly in the population of interest, the role for additional treatment or ‘rescue’ medication, and how the effect is expressed. The concept of estimands has been proposed as a way to bring such distinctions to the fore. An estimand is a more specific formulation of the comparison of interest being addressed. This thinking is reflected in a recent addendum to international regulatory guidelines for clinical trials of pharmaceuticals. Five main strategies are proposed. 23 Of particular note is the treatment policy strategy, which is consistent with what has often been described as an intention-to-treat (ITT)-based analysis. 22–25 That is, the ITT analysis addresses the difference between a policy of offering treatment with a given therapy and the policy of offering treatment with a different therapy, regardless of which treatments are received. Different stakeholders can have somewhat differing perspectives on the comparison of interest and therefore the estimand of primary interest. 22 Corresponding methods of analyses to address estimands that deviate from traditional conventional analyses are an active area of interest26 (see Appendix 3, Other topics of interest for a brief consideration of causal inference methods for dealing with non-compliance).
The target difference used in the sample size calculation should be one that at least addresses the trial’s primary objective and, therefore, the intended estimand of primary interest (with the corresponding implications for the handling of the receipt of treatment and population of interest). In some cases, it may be appropriate to ensure that the sample size is sufficient for more than one estimand, which might imply multiple target differences to address all key objectives. Different estimands may focus on different populations or subpopulations. Estimands will differ in their implications for the magnitude of missing data anticipated (see Appendix 3, Dealing with missing data for binary and continuous outcomes for how missing data can be taken into account in the sample size calculation in simple scenarios). Whatever the estimand of interest, the target difference is a key input into the sample size calculation.
Perspectives on the target difference of interest
Governmental/charity funder
Funders vary in the degree to which they will specify the research question. The primary concern is that the study provides value for money, by addressing a key research question in a robust manner and at reasonable cost to the funder’s stakeholders. This is typically an implicit consideration when the sample size and the target difference are determined. However, a very different approach, value of information (see Appendix 4), allows such wider considerations to be formally incorporated. The sample size calculation and the target difference, if well specified, provide reassurance that the trial will provide an answer to the primary research question, at least in terms of comparing the primary outcome between interventions. The specific criteria that proposals are invited to address, and are assessed against, vary among funders and individual schemes within a funder, as does the degree to which the research question may be a priori specified by the funder.
One particular aspect that varies substantially among funding schemes and funders is the extent to which they take into account the cost and cost-effectiveness of the interventions under consideration. Some funding schemes require the consideration of costs to come from a particular perspective; this might be the society as a whole or the health system alone. Alternatively, other schemes focus solely on clinical and patient perspectives, to greater or lesser extents.
All funders expect a RCT to have a sample size justification. 27 Typically, although not necessarily, this would be via a sample size calculation, most commonly based on the specification of a target difference. The specified target difference would be expected to be one that is of interest to their stakeholders; this is typically patients and health professionals, and sometimes the likely funder of the health care (e.g. the NHS in the UK). For industry-funded trials, the considerations are different and these are outlined in the next section (see Industry, payers and regulator).
The practical implications of an overly large trial are perhaps mostly financial (the funder has paid more than necessary to get an answer to the research question and thus there is less available for other trials). However, it is also ethically important to avoid more patients than necessary possibly receiving a suboptimal treatment, or simply to avoid unnecessary burden on further individuals and to avoid losing the opportunity to devote scarce resource funds to other desirable research. What is and is not sufficient in statistical and more general terms is often very difficult to differentiate, except in extreme scenarios. A trial that is too small is at risk of missing an effect. The funder could also later use the target difference in the context of evaluating (formally or informally) whether or not to close a study due to the probability (or lack thereof) of providing a useful answer in the face of substantially slower progression partway through a trial’s recruitment period.
Industry, payers and regulator
Industry-funded trials are typically (but not always) conducted as part of a regulatory submission for a new drug or medical device, or to widen the indications of an existing drug or device. Generally, an active intervention is compared with a placebo control, as this addresses the regulatory question of whether or not the intervention ‘works’. The main exception would be situations in which a new drug is intended to replace an established effective drug, in which case the established drug would be the control. An example is the evaluation of the newer oral anticoagulants, which have been compared with active comparators, such as warfarin or low-molecular-weight heparin, in the submissions for approval.
From an industry perspective, the target difference is often one chosen so that it is important to regulators and health-care commissioners. The key aspects of interest tend to be safety, including tolerability of treatment and consideration of side effects, whether or not the treatment is stopped due to a lack of effect and the effect within those who complete treatment. This has corresponding implications for the estimand(s) of interest. 22,23 Increasingly, payers (health insurance companies and governmental reimbursement agencies) are interested in comparisons with other active therapies, reflecting the need to inform treatment choices in actual clinical practice and considerations of affordability and cost-effectiveness. A new product will be more likely to be reimbursed if there are clinical advantages over existing therapies, in terms of either efficacy or adverse effect profiles, which are provided at an ‘acceptable’ cost. When an intervention is compared with an active control, the treatment effect between them will almost certainly be smaller and the sample size larger than for a placebo-controlled trial, all other things being equal. One common distinguishing feature between a definitive trial (e.g. Phase III) conducted in an industry setting, compared with an academic one, is that all of the evidence pertinent to planning such a trial of a new drug agent will often be readily available within the same company. It is also likely that at least some of the individuals involved will have been involved in a related earlier phase trial of the same drug.
Patient, service users, carers and the public
From the perspective of patients, service users, carers and the public,28 when a formal sample size calculation is performed, the target difference should be one that would be viewed as important by a key stakeholder group (such as health professionals, regulators, health-care funders and preferably patients). A specific point of interest, for those who serve as PPI contributors on research boards, who make funding recommendations and/or assess trial proposals, is likely to be ensuring that the study has considered the most patient-relevant outcome (e.g. a patient-reported outcome), even if it is not the primary outcome. In some situations, the most appropriate primary outcome may be a patient-reported outcome (e.g. comparing treatments for osteoarthritis, in which pain and function are the key measures of treatment benefit). It is highly desirable that a patient, service user and carer perspective feeds into the process for choosing the primary outcome in some way and, when possible, the chosen target difference reflects one that would have a meaningful impact on patient health, according to the research question. Some funders now require at least some PPI in the development of trial proposals and this perspective forms part of the assessment process. 28 It is also increasingly part of the assessment process for assessing existing evidence. 29
Research ethics
Fundamental to the standard ethical justification for the conduct of a RCT, which is a scientific experiment on humans, is (1) that it will contribute to scientific understanding and (2) that the participant is aware of what the study entails and, whenever possible, provides consent to participate. 30,31 Commonly, a third condition, that the participant has the potential to benefit, is also appropriate; this is particularly the case when there may be some risk to the participant. Whatever the specifics of the trial in terms of population, setting, interventions and assessments, it is important that the sample size for a study is appropriate to achieve its aim. There is a need for justification of some form for the number of participants required. As noted earlier, no more participants than ‘necessary’ should be recruited, to avoid unnecessary exposure to a suboptimal treatment and/or the practical burden of participation in a research study. Such a sample size justification may take the form of informal heuristics or, more commonly, a formal sample size calculation.
Clarifying what the study is aiming to achieve and determining an appropriate target difference and sample size is very important, as the research can have a big impact not only on those directly involved as participants, but also on future patients. As far as possible, it is also relevant to consider key patient subgroups or subpopulations of individuals in terms of relevance of findings to them. This could be taken into account when undertaking the sample size calculation (see Appendix 3).
The primary outcome of a randomised controlled trial
The role of the primary outcome
The standard approach to a RCT is for one outcome to be assigned as the primary outcome. 10 This is done by considering the outcomes that should be measured in the study. 32 The outcome is ‘primary’ in the sense of it being more important than the others, at least in terms of the design of the trial, although preferably it is also the most important outcome to the stakeholders with respect to the research question being posed. The study sample size is then determined for the primary outcome. As noted earlier, it is important to consider how the primary outcome relates to the population of interest and intervention effects to be estimated (the estimand of interest). Choosing a primary outcome (and giving it prominence in the statistical analysis of the estimands of interest) performs a number of functions in terms of trial design, but it is clearly a pragmatic simplification to aid the interpretation and use of RCT findings. It provides clarification of what the study primarily aims to use to identify the intervention effects. The statistical precision with which this can be achieved is then calculated according to the analysis of interest. Additionally, it clarifies the initial basis on which to judge the study findings. Specification of the primary outcome in the study protocol (and similarly reporting it on a trial registry) helps reduce overinterpretation of findings. This arises from testing multiple outcomes and selectively reporting those that are statistically significant (irrespective of their clinical relevance). This multiple testing, or multiplicity,33,34 is particularly important, given the high likelihood of chance leading to spurious statistically significant findings when a large number of outcomes are analysed. Pre-specification of a primary outcome, along with the use of a statistical analysis plan and transparent reporting (e.g. making the trial protocol available), limits the scope for manipulating (intentionally or not) the findings of the study. This prevents post hoc shifting of the focus (e.g. in study reports) to maximise statistical significance.
Choosing the primary outcome
A variety of factors need to be considered when choosing a primary outcome. First, in principle, the primary outcome should, as noted above, be a ‘key’ outcome, such that knowledge of its result would help answer the research question. For example, in a RCT comparing treatment with eye drops to lower ocular pressure with a placebo for patients with high eye pressure (the key treatable risk factor for glaucoma, a progressive eye disease that can lead to blindness), loss of vision is a natural choice for the primary outcome. 35 However, it would clearly be important to consider other outcomes (e.g. side effects of the eye drop drug). Nevertheless, knowing that the eye drops reduced the loss of vision due to glaucoma would be a key piece of knowledge. In some circumstances, the preferable outcome will not be used because of other considerations. In this glaucoma example, a surrogate might be used (intraocular pressure, i.e. pressure in the eye) because of the time it takes to measure any change in vision noticeable to a patient and also because this may enable prevention or at least a reduction in the degree of vision loss. Indeed, intraocular pressure is sometimes the primary outcome of RCTs in this area instead of vision or the visual quality of life.
Consideration is also needed of the ability to measure the chosen primary outcome reliably and routinely within the context of the study. Missing data are a threat to the usefulness of an analysis of any study, and RCTs are no different. The optimal mode of measurement may be impractical or even unethical. The most reliable way to measure intraocular pressure is through manometry;36 however, this requires invasive eye surgery. Subjecting participants to clinically unnecessary surgery for the purpose of a RCT is ethical only with very strong mitigating circumstances, particularly as an alternative, even if less accurate, way of measuring intraocular pressure exists. Furthermore, invasive measurements may dissuade participants from consenting to take part in the RCT.
Calculating the sample size varies depending on the outcome and the intended analysis. In some situations, ensuring that the sample size is sufficient for multiple outcomes is appropriate. 37 The three most common outcome types are binary, continuous and survival (time-to-event) outcomes; they are briefly considered in Box 2 and in greater depth in Appendix 3. Other outcome types are not considered here, although it should be noted that ordinal, categorical and count outcomes can be used, although a more complex analysis and corresponding sample size calculation approach is likely to be needed. Continuous outcomes (or a transformed version of them) are typically assumed to be normally distributed, or at least ‘approximately’ so, for ease and interpretability of analysis and for the sample size calculation. This assumption may be inappropriate for some outcomes, such as operation time, hospital stay and costs, which often have very skewed distributions. From a purely statistical perspective, a continuous outcome should not be converted to a binary outcome (e.g. converting a quality-of-life score to high/low quality of life). Such a dichotomisation would result in less statistical precision and lead to a larger sample size being required. 40 If it is viewed as necessary to aid interpretability, the target difference (and corresponding analysis) used in the continuous measure can also be represented as a dichotomy, in addition to being expressed on its continuous scale. Some authors, although acknowledging that this should not be routine, would make an exception in some circumstances when a dichotomy is seen as providing a substantive gain in interpretability, even if it is at a loss of statistical precision. 41 For example, the severity of depression may be measured and analysed on a latent scale, but the proportion of individuals meeting a prespecified threshold for depression or improvement might also be reported and potentially analysed. 42
The three most common outcome types (binary, continuous and time to event) are briefly described below.
BinaryA binary outcome is one with only two possible values (e.g. cured or not, and dead or alive). In terms of trials, they are usually time-bound (i.e. whether or not a participant is alive at 6 months post randomisation). Use of the date of the change in status (e.g. time of death) would lead to a survival or time-to-event outcome. Other common trial binary outcomes are the occurrence of an adverse event (e.g. surgical complication or a pharmacological event such as dryness of mouth).
ContinuousContinuous outcomes refer to those that have a numeric scale. True continuous measures (such as blood pressure measurements) have an infinite number of possible values. For example, a value of 125.2334456 mmHg for the systolic blood pressure is theoretically possible, even if it is difficult to measure it with such precision. Ordinal outcomes (with a sufficient number of discrete values) are often analysed as if they were continuous, owing to the difficulties of both calculating the required sample size and also interpreting the result from a more formal, statistically appropriate, analysis of an ordinal outcome. This is often done when analysing quality-of-life measures,38 in which a latent summary scale is produced by applying a scoring algorithm to responses to a set of items, even though there are a fixed number of discrete states (e.g. there are 243 for the EQ-5D-3L index with values from –0.594 to 1.0, using the UK population weights). The difficulty of calculating the sample size for an ordinal variable increases quickly as the number of responses increases. 39
Time to eventTime-to-event data are often called ‘survival’ data; a common application is for recording the time to death. However, the same statistical methodology can be used to analyse the time to any event. Examples include disease progression, readmission to hospital and wound healing, and positive ones such as time to full recovery.
Time-to-event data present two special problems in their analysis and hence in sample size estimation:
-
Not all participants have an event.
-
Participants are observed for varying amounts of time.
If all participants experience an event within the follow-up period, the data could be analysed as a continuous variable. In clinical studies, including RCTs, it is natural for participants to be observed for varying lengths of time. There are two reasons for this:
-
Some participants drop out before the end of follow-up.
-
Participants are recruited at different times.
Some participants drop out before the end of follow-up because they decline to take further part in the trial or because they experience some other event that means that they can no longer be followed up. For example, in a trial in which the event of interest is death from a cardiovascular cause, a participant who died in a road traffic accident would become unavailable for further follow-up and would be censored at the time of death.
If participants are followed up from recruitment to the final analysis, some will have been observed for a much longer time than others. In most clinical studies, this is the most frequent reason for varying durations of follow-up. The varying time of follow-up is the main reason why simply analysing the proportion of participants who experience an event (i.e. analyse it as if it were a binary outcome) is not appropriate.
EQ-5D-3L, EuroQol-5 Dimensions, three-level version.
Chapter 3 Specifying the target difference
General considerations
Introduction
Despite its key role, the specification of the target difference for a RCT has received surprisingly little discussion in the literature and in existing guidelines for conducting clinical trials. 10,14 As noted above, the target difference is the difference between the interventions in the primary outcome used in the sample size calculation that the study is designed to reliably detect. If correctly specified, it provides reassurance (should the other assumptions be reasonable and the sample size met) that the study will be able to address the RCT’s main aim in terms of the primary outcome, the population of interest and the intervention effects. It can also aid interpretation of the study’s findings, particularly when justified in terms of what would be an important difference. The target difference therefore should be one that is appropriate for the planned principal analysis (i.e. the estimand that is to be estimated and the analysis method to be used to achieve this). 23,25,43,44 This is typically (for superiority trials) what is known as an ITT-based analysis (i.e. according to the randomised groups irrespective of subsequent compliance with the treatment allocation). Other analyses that address different estimands22,25,44 of interest could also inform the sample size calculation (see Appendix 3, Other topics of interest for a related topic). How the target difference can be expressed will depend also on the planned statistical analysis. A target difference for a continuous outcome could be expressed as a difference in means, medians or even as a difference in distribution. Binary outcomes could be expressed as an absolute difference in proportions or as a relative difference [e.g. odds ratio (OR) or risk ratio (RR)]. Irrespective of the outcome type, there are two main bases for specifying the target difference, one that is considered to be:
-
important to one or more stakeholder groups (e.g. health professionals or patients)
-
realistic (plausible), based on either existing evidence (e.g. seeking the best available estimates in the literature) and/or expert opinion.
Recommendations on how to go about specifying the target difference are provided in Box 3. A summary of the seven methods that can be used for specifying the target difference is provided in Methods for specifying the target difference.
The following are recommendations for specifying the target difference in a RCT’s sample size calculation when the conventional approach to the sample size calculation is used. Recommendations on the use (or not) of individual methods are made. More detailed advice on the application of the individual methods can be found elsewhere. 15
Recommendations-
Begin by searching for relevant literature to inform the specification of the target difference. Relevant literature can:
-
relate to a candidate primary outcome and/or the comparison of interest
-
inform what is an important and/or realistic difference for that outcome, comparison and population (estimand of interest).
-
-
Candidate primary outcomes should be considered in turn and the corresponding sample size explored. When multiple candidate outcomes are considered, the choice of primary outcome and target difference should be based on consideration of the views of relevant stakeholders groups (e.g. patients), as well as the practicality of undertaking such a study and the required sample size. The choice should not be based solely on which yields the minimum sample size. Ideally, the final sample size will be sufficient for all key outcomes, although this is not always practical.
-
The importance of observing a particular magnitude of a difference in an outcome, with the exception of mortality and other serious adverse events, cannot be presumed to be self-evident. Therefore, the target difference for all other outcomes requires additional justification to infer importance to a stakeholder group.
-
The target difference for a definitive (e.g. Phase III) trial should be one considered to be important to at least one key stakeholder group.
-
The target difference does not necessarily have to be the minimum value that would be considered important if a larger difference is considered a realistic possibility or would be necessary to alter practice.
-
When additional research is needed to inform what would be an important difference, the anchor and opinion-seeking methods are to be favoured. The distribution should not be used. Specifying the target difference based solely on a SES approach should be considered a last resort, although it may be helpful as a secondary approach.
-
When additional research is needed to inform what would be a realistic difference, the opinion-seeking and review of the evidence-based methods are recommended. Pilot studies are typically too small to inform what would be a realistic difference and primarily address other aspects of trial design and conduct.
-
Use existing studies to inform the value of key ‘nuisance’ parameters that are part of the sample size calculation. For example, a pilot trial can be used to inform the choice of SD value for a continuous outcome or the control group proportion for a binary outcome, along with other relevant inputs, such as the number of missing outcome data.
-
Sensitivity analyses that consider the impact of uncertainty around key inputs (e.g. the target difference and the control group proportion for a binary outcome) used in the sample size calculation should be carried out.
-
Specification of the sample size calculation, including the target difference, should be reported in accordance with the recommendations for reporting items (see Chapter 4, Figure 1) when preparing key trial documents (grant applications, protocols and result manuscripts).
SD, standard deviation; SES, standardised effect size.
A very large literature exists on defining a (clinically) important difference, particularly for quality-of-life outcomes. 45–47 Much of the focus has been on estimating the smallest value that would be considered clinically important by stakeholders [the ‘minimum clinically important difference’ (MCID)]. 45–48 In a similar manner, discussion of the relevance of estimates from existing studies are also common occurrences. It should be noted that it has been argued that a target difference should always meet both of the above criteria. 49 This would seem particularly apt for a definitive Phase III RCT. There is some confusion in the reporting of sample size calculations for trials in the literature and what the use of a particular approach justifies. For example, using data from previous studies (see Pilot studies and Review of the evidence base) cannot by itself inform the importance, or lack thereof, of a particular difference.
The subsequent sections (see Individual- versus population-level important differences and Reverse engineering) consider two special topics, individual- and population-level important difference and reverse engineering of the sample size calculation, respectively.
Individual- versus population-level important differences
In a RCT sample size calculation, the target difference between the treatment groups strictly relates to the difference at the group level. In a similar manner, the health economic consideration refers to how to manage a population of individuals in an efficient and effective manner. However, the difference in an outcome that is important to an individual is not necessarily the same difference that might be viewed as important at the population level. Rose50 grappled with the meaning and relationships between individual- and population-level differences, and their implications, in the context of disease prevention. He noted that, based on data from the Framingham Heart Study,51 an average 10-mmHg lowering of blood pressure could potentially result in a 30% reduction in attributable mortality. Although a 10-mmHg change in an individual might seem small, if a treatment could achieve that average difference, it would be very beneficial. A 10-mmHg change could therefore be justified as an appropriate and important target difference for a trial in a similar population. An individual may wish a greater impact, particularly if the intervention they are to receive is burdensome or carries some risk.
More recently, researchers in other clinical areas have also distinguished between what is ‘important’ at an individual level and what is ‘important’ at a group level for quality-of-life measures. 52–54 In a RCT sample size calculation, the parameters assumed for the outcome in the intervention groups in the sample size calculation, including the target difference, should reflect the population-level values (e.g. the mean difference in Oxford Knee Score), even though individual values can vary. 55 When considering the importance of and/or how realistic a specific difference is, the intended trial population must be borne in mind. The difference that would be considered important by patients may well vary between populations (e.g. according to the severity of osteoarthritis). 56 For example, the importance of a 5-point increase (improvement) in the Oxford Knee Score for a relatively healthy population, with a mean baseline level of 30 points (out of 48), could well differ from that of a population that has severe osteoarthritis, with a mean baseline level of 10 points. Similarly, in terms of population risk (e.g. risk of a stroke), a small reduction at a population level might be considered very important, whereas for a group of high-risk patients, a more substantial reduction may be required. 50
Work has shown that individuals differ in what magnitude of difference they consider important, at least in part due to their varying baseline levels. 18,45 This general issue has implications when selecting a target difference, as it should be a difference that reflects the analysis at the group (and intended population) level and the comparison at hand. Care is therefore needed when using values from external studies to infer an important difference.
Reverse engineering
The difference that can be detected for a given sample size is often calculated. It can be apparent that this has been done (e.g. when one sees a precise target difference and a round sample size) without any other justification. For example, a target difference of 16.98 for a trial with a pooled standard deviation (SD) of 30, statistical power of 80% at two-sided 5% significance level and two treatment groups of 100 participants has clearly been reverse engineered.
A key distinction needs to be made between calculating the target difference for a prospective trial from calculating the target difference on the basis of the recruited sample size once the trial has been completed (post hoc power calculation). The former has a useful role in the process of planning and deciding what is feasible; the latter is unhelpful and uninformative. 57
Case study 6 describes a situation in which a fixed (and complete) number of observations were expected without loss due to consent or attrition-driven subsampling, but the corresponding target difference was calculated and deemed to be an important and realistic difference to use.
Methods for specifying the target difference
The methods for specifying the target difference can be broadly grouped into seven types. These are briefly described below.
Anchor
The quantification of a target difference or effect size for a sample size calculation is not straightforward for an established end-point or outcome measure. 58 For a new outcome, especially a patient-reported health-related quality-of-life measure, it is even more difficult, as clinical experience with using the new outcome may not have been sufficiently long to evaluate what a clinically meaningful or important difference might be. Additionally, for a measure such as a quality-of-life outcome, the scale has no natural meaning and is completely a function of the scoring method (i.e. a 1-point difference does not have any naturally interpretable value).
The outcome of interest can, however, be ‘anchored’ by using someone’s judgement, typically a patient or a health professional, to define what an important difference is. 46–48 This is typically achieved by comparing a patient’s health before and after a recognised treatment, and then linking the change to participants who showed improvement and/or deterioration according to the judgement of changes (e.g. on a five-point Likert scale from ‘substantial deterioration’ through to ‘substantial improvement’). Alternatively, a more familiar outcome (for which patients or health professionals more readily agree on what amount of change constitutes an important difference) can be used. In this way, one outcome is anchored to another outcome about which more is known. Contrasts between patients (such as individuals with varying severity of a disease) can also be used to determine a meaningful difference (e.g. via patient-to-patient assessments). 20,59
The Food and Drug Administration has described a variety of methods for determining the minimum important difference, including the anchor approach. 7 Changes in quality-of-life measures can be mapped to clinically relevant and important changes in non-quality-of-life measures of treatment outcome in the condition of interest (although they may not correlate strongly). 60 There are a multitude of minor variations in the approach (e.g. the anchor question and responses, or how the responses are used), although the general principles are the same. 15,46–48
Distribution
Two distinct distribution approaches can be grouped under this heading:15,45 (1) measurement error and (2) rule of thumb. The measurement error approach determines a value that is larger than the inherent imprecision in the measurement and that is therefore likely to be consistently noticed by patients. This is often based on the standard error of measurement. The standard error of measurement can be defined in various ways, with different multiplicative factors suggested as signifying a non-trivial (important) difference. The most commonly used alternative to the standard error of measurement method (although it can be thought of as an extension of this approach) is the reliable change index proposed by Jacobson and Truax,61 which incorporates confidence around the measurement error.
The rule-of-thumb approach defines an important difference based on the distribution of the outcome, such as using a substantial fraction of the possible range without further justification. An example would be viewing a 10-mm change on a 100-mm visual analogue scale measuring symptom severity as a substantial shift in outcome response.
Measurement error and rule-of-thumb approaches are widely used in the area of measurement properties of quality of life, but do not translate straightforwardly to a RCT target difference. For measurement error approaches, this is because the assessment is typically based on test–retest (within-person) data, whereas most trials are of parallel-group (between-person) design. Additionally, measurement error is not sufficient rationale as the sole basis for determining the importance of a particular target difference. More generally, the setting and timing of data collection may also be important to the calculation of measurement error (e.g. results may vary between pre and post treatment). 62 Rule-of-thumb approaches are dependent on the outcome having inherent value (e.g. the Glasgow Coma Scale score), in which a substantial fraction of a unit change (e.g. one-third or a half) can be viewed as important. In this situation, any reduction is arguably also important and the issue is more one of research practicality (as per mortality outcome) than detecting a clinically important difference.
Distribution approaches are not recommended for use to inform the choice of the target difference, given their inherently arbitrary nature in this context.
Health economic
Approaches to using economic evaluation methodology to inform the design of RCTs have been proposed since the early 1990s. 63,64 These earlier approaches sought to identify threshold values for key determinants of cost-effectiveness and are akin to determining an important difference in clinical outcomes, albeit on a cost-effectiveness scale. However, uptake has been very low. A recent review by Hollingworth and colleagues65 identified only one study that considered cost-effectiveness in the sample size calculation. They also showed that trials powered on clinical end points were less likely to reach definitive conclusions of cost-effectiveness than on clinical effectiveness.
Despite the lack of use, further development of methods has continued. A strand in the development of these methods has been to focus on a variation in the standard frequentist approach to sample size estimation. The most recent exposition of this was by Glick. 66,67 Glick focused on a particular economic metric, the incremental net benefit (INB) statistic. A key aspect of the INB is that it monetarises a unit of health effect by multiplying it by the decision-maker’s willingness to pay for that unit of health effect. Power is taken to be the chance that the lower limit of the confidence interval (CI) calculated from the future trial exceeds 0. An important difference is then any difference in INB that is ≥ 0, and the size of the trial can be set so as to detect this. However, Glick notes that willingness to pay is not known for certain (e.g. in England, the National Institute for Health and Care Excellence68 currently specifies a range of between £20,000 and £30,000 per quality-adjusted life-year gained) and that, other things being equal, increasing the decision-maker’s willingness to pay for a unit of health effect reduces the sample size. An alternative economics-based approach, value of information, is summarised in Appendix 4.
Opinion-seeking
The opinion-seeking method determines a value, a range of plausible values, or a prior distribution for the target difference by asking one or more ‘experts’ to state their opinion on what value(s) for a particular difference would be important and/or realistic. 69,70 Eliciting opinions on the relative importance of the benefits and risks of a medicine may also be used to inform the choice of non-inferiority or equivalence margins for such trials. 71,72
The definition of an expert (e.g. clinician, patient or triallist) must be tailored to the quantity on which an opinion is sought. Various approaches can be used to identify experts (e.g. key opinion leaders, literature search, mailing list or conference attendance). Other variations include the approach used to elicit opinion (e.g. group and/or individual interviews, questionnaires, e-mail surveys or workshops),73–75 the complexity of the data elicited (from a single value76 to multiple assessments incorporating uncertainty77 and/or sensitivity to key factors, such as baseline level78) and the method used to consolidate the results into an overall value, range of values or distribution. 69
Many elicitation techniques have been developed in the context of Bayesian statistics to establish a prior distribution, quantifying an expert’s uncertainty about the true treatment difference. 69 The expert will be asked a series of questions to elicit a number of summaries of their prior distribution. The number and nature of these summaries will depend on the nature of the treatment difference (i.e. whether or not this is a difference in means, RR, etc.) and what parametric distribution (if any) will be used to model the expert’s prior. Typically, more summaries are elicited than are strictly necessary, to enable model checking. Feedback of the fitted prior is an essential part of the elicitation process to ensure that it adequately captures the expert’s beliefs. Examples of prior elicitation include the Continuous Hyperfractionated Accelerated RadioTherapy (CHART) and MYcophenolate mofetil for childhood PAN (MYPAN) trials. 77,79,80 When the opinions of several experts are elicited, several priors may be used to capture a spectrum of beliefs (e.g. sceptical, neutral or enthusiastic). Priors may be used to inform the design of a conventional trial (e.g. when setting the sample size or an early stopping rule),79,81 to ensure that the study would convince a prior sceptic. Alternatively, priors may be incorporated into the interpretation of a Bayesian trial to reduce uncertainty, which may be appropriate in cases such as rare diseases, when a conventionally powered study is infeasible. 82 Bayesian approaches to sample size calculations are discussed in more detail in Appendix 4.
An advantage of the opinion-seeking method is the relative ease with which it can be carried out in its simpler forms. 78 However, the complexity increases substantially when undertaken as a formal elicitation. 77 Whatever the approach used, it should ideally match, as closely as possible, the intended trial research question. 73,78,83 Findings will vary according to the patient population and comparison of interest. Additionally, different perspectives (e.g. patient vs. health professional) may lead to very different opinions on what is important and/or realistic. 83 The views of individuals who participate in the elicitation process may not represent those of the wider community. Furthermore, some methods for eliciting opinions have cost or feasibility constraints (e.g. those requiring face-to-face interaction). However, alternative approaches, better able to capture the views of a larger number of experts, require careful planning to ensure that questions are clearly understood. Care is needed with these approaches, as they may be subject to low response rates78 or may produce priors with limited face validity.
Pilot studies
Pilot studies come in various forms. 84 A useful distinction can be made between pilot studies, per se, and the subset of pilot studies (pilot trials) that can be defined as an attempt to pilot the study methodology prior to conducting the main trial. As such, data from a pilot trial are likely to be directly relevant to the main trial. This section therefore focuses on pilot trials, although the considerations are relevant to other pilot studies that have not been designed with a particular trial design in mind. It should be noted that some Phase II trials can be viewed in a similar manner as preparing for a Phase III trial and therefore can inform sample size calculations.
Pilot trials are not well suited to quantifying a treatment effect, as they usually have a small sample size and are not typically large enough to quantify, with much certainty, what a realistic difference would be. 85 Accordingly, avoiding conducting formal statistical testing and focusing instead on descriptive findings and interval estimation is recommended. 84,86 In terms of specifying the target difference for the main trial, pilot trials are most useful in providing estimates of the associated ‘nuisance’ parameters (e.g. SD and control group event proportion; see Chapter 5, Case study 2: the ACL-SNNAP trial, for more details). 84,87 Like any quantity, these parameters will, however, be estimated with uncertainty, which has implications for the sample size of both a pilot trial and a subsequent main trial. 88
Another use of a pilot trial is to assess the plausibility (at a less exacting level of statistical certainty than would be typically required for a main trial) of a given difference considered to be important through the calculation of a CI. 87 Pilot trial-based CIs can be considered investigative and can be used to help inform decision-making. If an effect of this size is not ruled out by the CI of the estimated effect from the pilot trial, then results could be deemed sufficiently promising to progress to the main trial. 86,89
Review of the evidence base
An alternative to conducting a pilot trial is to review existing studies to assess a realistic effect and therefore inform the choice of target difference for the main trial. 15 Pre-existing studies for a specific research question can be used (e.g. using the pooled estimate of a meta-analysis) to determine the realistic difference. 14 It has been argued strongly and persuasively that this should be routine prior to embarking on a new trial. 90 Extending this general approach, Sutton and colleagues91,92 derived a distribution for the effect of a treatment from a meta-analysis, from which they then simulated the effect of a ‘new’ study; the result of this study was added to the existing meta-analysis data, which were then reanalysed. Implicitly, this adopts a realistic difference as the basis for the target difference and therefore makes no judgement about the value of the effect should it truly exist. Using the same target difference as a previous trial, although heuristically convenient, does not provide any real justification, as it may or may not have been appropriate when used in the last study.
It is likely that existing evidence is often informally used (indeed, research funders typically require a summary of existing evidence prior to commissioning a new study), although little research has addressed how it should formally be done. Estimates identified from existing evidence may not necessarily be appropriate for the population and estimand under consideration for the trial, so the generalisability of the available studies and susceptibility to bias should be considered. Indeed, the planning of a new study implies some perceived limitation in the existing literature. Imprecision of the estimate is also an important consideration and publication bias may also be an issue if reviews of the evidence base consider only published data. If a meta-analysis of previous studies is used to inform the sample size calculation for a new trial, additional evidence published after the search used in the meta-analysis was conducted may require the updating of the sample size calculation during trial conduct, to maintain a realistic difference. The control group proportion or the SD (as well as other inputs that influence the overall sample size) can be estimated using existing evidence. An analysis that also makes use of other studies (existing or ongoing) can provide a sample size justification for what may be otherwise too small a study to provide, on its own, a useful result. 93
Standardised effect size
The magnitude of the target difference on a standardised scale [standardised effect size (SES)] is commonly used to infer the value of detecting this difference when set in comparison with other possible standardised effects. 15,85 Overwhelmingly, the practice for RCTs, and in other contexts in which the (clinical) importance of a difference is of interest, is to use the guidelines suggested by Cohen94 for Cohen’s d metric (i.e. 0.2, 0.5 and 0.8 for small, medium and large effects, respectively) as de facto justification. These values were given in the context of a continuous outcome for a between-group comparison (akin to a parallel-group trial), with the caveat that they are specific to the context of social science experiments. Despite this, due in part to having some face validity and in part to the absence of a viable or ready alternative, justification of a target difference on this basis is widespread. Colloquially, and rather imprecisely, Cohen’s d value is often described as the trial ‘effect size’.
Other SES metrics exist for continuous (e.g. Dunlap’s d), binary (e.g. OR) and survival [hazard ratio (HR)] outcomes, and a similar approach can be readily adapted for other types of outcomes. 94,95 The Cohen guidelines for small, medium and large effects can be converted into equivalent values for other binary metrics (e.g. 1.44, 2.48 and 4.27, respectively, for ORs). 96 Guidelines for other effect sizes exist (including some suggested by Cohen94). Informally, a doubling or halving of a ratio is sometimes seen as a marker of a large relative effect. However, no equivalent guideline values are in widespread use for any of the other effect sizes. In the case of relative effect metrics (such as the RR), this probably reflects the difficulty in considering a relative effect apart from the control group response level.
The main benefit of using a SES method is that it can be readily calculated and compared across different outcomes, conditions, studies, settings and people; all differences are translated into a common metric. It is also easy to calculate the SES from existing evidence if studies have reported sufficient information. When calculated, the SD (or equivalent inputs) used should reflect the intended estimand (i.e. the population and outcome).
It is important to note that SES values are not uniquely defined and different combinations of values on the original scale can produce the same SES value. For example, different combinations of mean and SD values produce the same Cohen’s d statistic SES estimate. A mean of 5 (SD 10) and a mean of 2 (SD 4) both give a standardised effect of 0.5 SDs. As a consequence, specifying the target difference as a SES alone, although sufficient in terms of sample size calculation, can be viewed as insufficient, in that it does not actually define the target difference for the outcome measure of interest in the population of interest. A further limitation of the SES is the difficulty in determining why different effect sizes are seen in different studies, for example whether these differences are due to differences in the outcome measure, intervention, settings or participants in the studies, or study methodology. This approach should be viewed as, at best, a last resort. It is perhaps more useful (for a continuous outcome) to provide a benchmark to assess the value from another method. Preferably, some idea of effect sizes for an accepted treatment in the specific clinical area of interest would be available. 97
Chapter 4 Reporting of the sample size calculation for a randomised controlled trial
The approach taken and the corresponding assumptions made in the sample size calculation should be clearly specified, as well as all inputs and formula so that the basis on which the sample size was determined is clear. This information is critical for reporting transparently, allows the sample size calculation to be replicated and clarifies the primary (statistical) aim of the study. A recommended list of reporting items for recording in key trial documents (grant applications, protocols and results paper) is provided in Figure 1, for when the conventional approach to sample size calculation has been used. When another approach has been used, appropriate items should be reported sufficient to ensure transparency and allow replication.
FIGURE 1.
Recommended DELTA2 reporting items for the sample size calculation of a RCT with a superiority question. ICC, intracluster correlation.

Core items sufficient to replicate the sample size calculation should be provided in all key documents. Under the conventional approach with a standard (1 : 1 allocation two-arm parallel-group) trial design and unadjusted statistical analysis, the core items that should be stated are the primary outcome; target difference, appropriately specified according to the outcome type; associated nuisance parameters; and statistical significance and power. Specification of the target difference in the sample size calculation section varies according to the type of primary outcome. The expected (predicted) width of the CI can be determined for a given target difference and sample size calculation, and can be a helpful further aid in making an informed choice about this part of a trial’s design and could also be reported. 98
When the calculation deviates from the conventional approach (see Appendix 3), whether by research question or statistical framework, this should be clearly specified. Formal adjustment of the significance level for multiple outcomes, comparisons or interim analyses should be specified. 33,34,37,99 Justification for all input values assumed should be provided.
We recommend that trial protocols and grant applications report additional information, explicitly clarifying the basis used for specifying the target difference and the methods/existing studies used to inform the specification of the target difference. Examples of a trial protocol sample size section under a conventional approach to the sample size calculation for a standard trial and unadjusted analysis are provided in Boxes 4–6 for binary, continuous and time-to-event primary outcomes, respectively. The word counts for these texts are 74–125 words, illustrating that key information can be conveyed in a limited amount of text.
The primary outcome is presence of urinary incontinence. The sample size is based on a target difference of 15% absolute difference (85% vs. 70%) at 12 months post randomisation. This magnitude of target difference was determined to be both a realistic and an important difference from discussion between clinicians and the project management group, and from inspection of the proportion of urinary continence in the trials included in a Cochrane systematic review. 101 The control group proportion (70%) is also based on the observed proportion in the RCTs in this review. Setting the statistical significance to the two-sided 5% level and seeking 90% power, 174 participants per group are required, giving a total of 348 participants. Allowing for 13% missing data leads to 200 per group (400 participants overall).
Reproduced from Cook et al. 14 Contains information licensed under the Non-Commercial Government Licence v2.0.
The primary outcome is Early Treatment Diabetic Retinopathy Study (ETDRS) distance visual acuity. 103 A target difference of a mean difference of five letters with a common SD of 12 at 6 months post surgery is assumed. Five letters is equivalent to one line on a visual acuity chart and is viewed as an important difference by patients and clinicians. The SD value is based on two previous studies – one observational comparative study104 and one RCT. 105 This target difference is equivalent to a SES of 0.42. Setting the statistical significance to the two-sided 5% level and seeking 90% power, 123 participants per group are required, giving 246 participants (274, allowing for 10% missing data) overall.
Reproduced from Cook et al. 14 Contains information licensed under the Non-Commercial Government Licence v2.0.
The primary outcome is all-cause mortality. The sample size was based on a target difference of 5% in 10-year mortality, with a control group mortality of 25%. Both the target difference and control group mortality proportions are realistic, based on a systematic review of observational (cohort) studies. 107 Setting the statistical significance to the two-sided 5% level and seeking 90% power, 1464 participants per group are required, giving a total of 2928 participants (651 events).
Reproduced from Cook et al. 14 Contains information licensed under the Non-Commercial Government Licence v2.0.
Owing to space restrictions, in many publications the main trial paper is likely to contain less detail than is desirable. Nevertheless, a minimum set of reporting items is recommended for the main trial results paper, along with full specification in the trial protocol. The trial results paper should reference the trial protocol, which should be made publicly available. The recommended list of items given in Figure 1 for the trial paper (as well as for the protocol) is more extensive than that in the Consolidated Standards of Reporting Trials (CONSORT) (including the 2010 version)108 and the Standard Protocol Items: Recommendations for Interventional Trials (SPIRIT)109 statements.
Chapter 5 Case studies of sample size calculations
Overview of the case studies
A variety of case studies are provided for different trial designs, including varying types of primary outcomes, availability of evidence to inform the target difference and level of complexity. A short description is provided in Table 1.
| Number | Description | Trial |
|---|---|---|
| 1 | A standard (two-arm parallel-group) trial, in which the opinion-seeking and review of the evidence-based methods were used to inform the target difference for a binary outcome | MAPS100 |
| 2 | A two-arm parallel-group trial, in which the anchor and distribution methods were used to inform the target difference for a continuous quality-of-life outcome | ACL-SNNAPa |
| 3 | A crossover trial, in which the opinion-seeking and review of the evidence base methods were used to inform the target difference for a binary patient-reported outcome | OPTION-DM110 |
| 4 | A three-arm parallel-group trial, in which the review of the evidence base was used to inform the target difference for a binary clinical outcome | SUSPEND111 |
| 5 | A three-arm/two-stage parallel-group trial, in which the anchor, review of the evidence base and SES methods were used to inform an important and realistic difference in a continuous quality-of-life outcome | MACRO112,113 |
| 6 | A two-arm cluster trial, in which the opinion-seeking and review of the evidence base methods were used to inform an important and realistic difference in a continuous cluster-level process measure outcome | RAPiD114 |
Case study 1: the MAPS trial
Radical prostatectomy is carried out for men suffering from early prostate cancer. The operation is usually carried out through an open incision in the abdomen, which may damage the urinary bladder sphincter, its nerve supply and other pelvic structures. Urinary incontinence occurs in around 90% of men initially, but the long-term prognosis varies from 2% to 60%, depending on how incontinence is measured and time after surgery. Successive Cochrane systematic reviews101 have shown that, although conservative treatment based on pelvic floor muscle training may be offered to men with urinary incontinence after prostate surgery, there is insufficient evidence to evaluate its effectiveness and cost-effectiveness. Men After Prostate Surgery (MAPS)100 was a multicentre RCT that aimed to assess the clinical effectiveness (primarily by looking at the presence of urinary incontinence post treatment) and cost-effectiveness of active conservative treatment delivered by a specialist continence physiotherapist or a specialist continence nurse, compared with standard management, in men receiving a radical prostatectomy at 12 months after surgery.
The primary outcome was the presence of urinary continence. No other outcomes were considered. The sample size was based on a target difference of 15% absolute difference (85% specialist treatment vs. 70% control). A Cochrane systematic review101 suggested that the current control group proportion was 70% (average across relevant control groups). This magnitude of target difference was determined to be both a realistic and an important difference from discussion between clinicians and the project management group, and from inspection of the proportion of patients with urinary continence in the trials included in the Cochrane systematic review. 101 Setting the statistical significance to the two-sided 5% level and seeking 90% power, 174 participants per group were required, giving a total of 348 participants prior to considering missing data. Allowing for just under 15% missing data increased the overall sample size to 400. The power (77%) should the control group response turn out to be 40% (i.e. using 55% for the treatment and 40% for the control) was calculated as a sensitivity analysis. As the power was still reasonably high and this was considered a less plausible scenario, the overall sample size was not changed (see Box 4).
Case study 2: the ACL-SNNAP trial
Anterior cruciate ligament (ACL) rupture is a common injury, mainly affecting young, active individuals. ACL injury can have a profound effect on knee kinematics (knee movement and forces), with recurrent knee instability (giving way) the main problem. In the UK, a surgical management strategy has become the preferred treatment for ACL-injured individuals. However, the preference for surgical management (reconstruction) of the ACL-deficient knee had been questioned by a Scandinavian trial,115 which suggested that rehabilitation can reduce the proportion of acute patients requiring surgery by up to 50%.
A two-arm RCT – ACL Surgery Necessity in Non Acute Patients (ACL-SNNAP)115 – was planned to compare a strategy of non-surgical management, with the option of surgery if required (the rehabilitation group), with a strategy of surgical management only (the reconstruction group) in the UK NHS setting treating non-acute patients. The main outcome of interest was the Knee injury and Osteoarthritis Outcome Score (KOOS)-4, which excludes the activities of daily living component of the full KOOS. This decision reflected belief about the impact of ACL rupture and the aim of treatment. 115,116 KOOS-4 seemed to be the most appropriate of the available condition-relevant quality-of-life measures.
Limited work had assessed what would be a minimum important difference (MID) in the overall KOOS and the KOOS-4 variant. The KOOS user guide recommended 8–10 points as the (current) best estimate of a minimum important change. 117 This was based on an anchor method approach, using clinical judgement about the recovery timescale applied to a small cohort of ACL reconstruction patients. 118 Differences that occurred within the recovery period were ≤ 7 points, whereas those that occurred afterwards were ≥ 8 points for three of the four KOOS-4 domain scores. Given the limited data on what would constitute an important difference, estimates from a distribution-based approach [minimum clinically detectable change (MCDC)] were also considered. The MCDC was around 6–12 for individual domains. 119 A value of 8 points was taken as a reasonable value for the MCID in the KOOS-4 overall score.
A standard sample size calculation for comparing two means using a SD of 19 gave a required sample size of 120 in each group, for 90% power at a two-sided 5% significance level. This is how many patients would be required for an individually randomised trial in the absence of any clustering of outcome. The impact of clustering of outcome by the main intervention deliverer (surgeon and/or physiotherapist) was also considered. Given the time of outcome measurement (quality of life at 6 months), previous evidence suggested any clustering effect to be low: circa 0–0.06 for intracluster correlation (ICC) effect estimates from a database of previous surgical trials. 121 Clustering was assumed to occur to the same degree in both arms. Two surgeons from at least 13 sites were anticipated, whereas a priori more physiotherapists (at least 50% more, i.e. around 40) were anticipated to be involved in the study. Credible SDs for the cluster sizes were informally assessed using mock scenarios. Equal allocation was planned.
The sample size was estimated to be 130 patients per group to achieve just over 80% power, based on assuming an ICC of 0.06. With 26 surgeons, the number of patients per surgeon in the surgery management arm was expected to be five on average. With 40 physiotherapists, the number of patients per physiotherapist was expected to be three on average. Some allowance for variance in the number per health professional was also made. Given the anticipated challenges in recruiting to the study, keeping the sample size as small as possible was considered critical. As clustering was not certain, the sample size was increased to ensure at least 80% power if clustering occurred. In the absence of clustering, the power would be > 90%.
To allow for missing data, the sample size was set at 320 (allowing approximately 15% loss to follow-up). The total required sample size was therefore 320 patients. As the funding agency requested an interim check on the degree of clustering, a single planned interim check was set once data for 100 patients had been collected. This planned interim assessment would assess only the ICC magnitude and other sample size assumptions, such as cluster size. A formal interim analysis comparing treatments was not planned. Box 7 provides the corresponding sample size explanation in the trial protocol.
A total of 320 participants will be recruited to the study. The minimum clinically important change (MIC) for the KOOS score is 8–10 points. 117 Estimates of the MCDC for the two KOOS subscales most relevant for ACL vary between 5 and 12 points (symptoms 5–9, and sport/recreation 6–12). 117 Conservatively, a target difference of 8 points and a SD of 19 points (the highest value observed in a trial of acute patients at baseline among the KOOS subscales) is assumed. Given these assumptions, 120 participants per group are required (240 in total) to achieve 90% power at a two-sided 5% significance level in the absence of any clustering of outcome.
To ensure sufficient power, clustering [clsampsi Stata® command120 (StataCorp LP, College Station, TX, USA)] has been allowed for by conservatively assuming an ICC of 0.06121 and cluster size n, mean (SD) of n = 26, mean = 5 (SD 12) and n = 43, mean = 3 (SD 5) for the ACL reconstruction and rehabilitation groups, respectively. Therefore, 130 participants are required per group (260 participants overall) to ensure just over 80% power. Given the conservative nature of the assumed values and the anticipated gain in precision from adjusting for the baseline scores and other randomisation factors, actual power is likely to be higher even in the presence of clustering.
To allow for just over 15% missing data (response in a similar trial116), 320 participants will be needed. An interim analysis will be carried out to estimate the magnitude of clustering for the 6 months KOOS-4 outcome once data are available for 100 participants. A decision whether or not the sample size should be increased to allow for a greater level of clustering than anticipated will be made based on the interim analysis.
Modified from www.fundingawards.nihr.ac.uk/award/14/140/63 (accessed October 2019).
Case study 3: the OPTION-DM trial
A common comorbidity for patients with diabetes mellitus is neuropathic pain. Although there are some pharmacological treatments for this pain, it is unclear which is best. As the first-line treatment often does not work, patients may get second-line treatments as part of a care pathway. In the Optimal Pathway for TreatIng neurOpathic paiN in Diabetes Mellitus (OPTION-DM) trial,110 three care pathways were to be compared in a three-period crossover study. All patients would receive all three patient pathways. Each care pathway reflected a form of clinical practice that a patient might receive for their neuropathic pain. The main candidate primary outcome was the 7-day-average 24-hour pain after 16 weeks of treatment, measured on a numeric rating scale.
There was some experience of using such a pain score within the study team and in the published literature:
-
A recent placebo-controlled crossover trial observed a 0.5-point average difference between the active comparator and placebo. 122
-
Patients in this population on the active treatment were expected to improve from baseline by, on average, 2 points.
-
A 1-point improvement within an individual patient was viewed as a clinically important difference, based on an existing study that used an opinion-seeking approach. 123
These criteria were used to inform the choice of a clinically important difference. The wish was to increase the proportion of patients improving by ≥ 1 point. The proportion of individuals improving can be calculated given the assumed reduction and difference between the groups. We expected a mean improvement of 2 points from baseline. Assuming that the change from baseline followed a normal distribution, 66% of patients were anticipated to improve by 1 point (relevant values are in bold text in Table 2).
| Cumulative proportion of individuals improving | Anticipated improvements from baseline | |
|---|---|---|
| 2-point reduction | 2.5-point reduction | |
| 0.50 | –2.00 | –2.50 |
| 0.52 | –1.88 | –2.38 |
| 0.54 | –1.77 | –2.27 |
| 0.56 | –1.65 | –2.15 |
| 0.58 | –1.53 | –2.03 |
| 0.60 | –1.41 | –1.91 |
| 0.62 | –1.29 | –1.79 |
| 0.64 | –1.16 | –1.66 |
| 0.66 | –1.04 | –1.54 |
| 0.68 | –0.91 | –1.41 |
| 0.70 | –0.78 | –1.28 |
| 0.72 | –0.64 | –1.14 |
| 0.74 | –0.50 | –1.00 |
If, for example, a clinically important mean difference of 0.5 points between treatments was the target (see bold text in Table 2 for relevant values), this would equate to a mean change from baseline of 2.5 points and 74% of patients showing a clinical improvement of ≥ 1 points in the active group. These calculations suggested a clinically important mean difference of 0.5 points, which we can equate to the proportion of individual patients showing individual clinical improvements of 1 point.
The calculation was then adjusted for multiplicity. Each care pathway was planned to be compared with each of the other pathways at the end of the trial. As three formal comparisons were planned, the Bonferroni adjustment was used to adjust the significance level to maintain an overall two-sided, 5% significance level. The sample size was calculated for 90% statistical power. See Box 8 for the corresponding sample size explanation presented in the protocol.
An individual showing a 1-point change in the numeric rating scale is considered a MCID. 123 Hence, the proportion of people improving by at least 1 point would seem a suitable outcome. However, we have based the sample size calculation on a continuous outcome, the mean change between groups, to maintain power. We have chosen a mean change between groups of 0.5 points based on the mean difference previously reported for a comparison of two active interventions for neuropathic pain in a crossover study. 122 We estimate this would equate to an 8% difference between groups in the proportion of people improving by at least 1 point. 58 Using a within-patient SD of 1.65,122 an alpha of 0.0167 (0.05/3) to allow for three comparisons and 90% power, we require 294 evaluable patients. 124
A total of 536 patients will be screened for participation in the study. Assuming a 25% dropout rate, 392 patients will be randomised to ensure that 294 patients are expected to complete the study.
Reproduced from Tesfaye et al. 110 Contains information licensed under the Non-Commercial Government Licence v2.0.
If the proportion of patients with an improvement of ≥ 1 point had been used as the primary outcome (i.e. dichotomising the pain score) and analysed accordingly as a binary outcome, for an effect of 8%, the corresponding sample size would have required a much larger sample size of 884 analysable patients (n = 1179, allowing for dropout).
Case study 4: the SUSPEND trial
Ureteric colic describes episodic severe abdominal pain from sustained contraction of ureteric smooth muscle as a kidney stone passes down the ureter into the bladder. It is a common reason for people to seek emergency health care. Treatments that increase the likelihood of stone passage would benefit patients with ureteric colic, as they will reduce the need for an interventional procedure.
At the time of planning, two smooth muscle relaxant drugs, tamsulosin (an alpha-adrenoceptor antagonist, or alpha-blocker) and nifedipine (a calcium channel blocker), known as medical expulsive therapy (MET), were considered potentially beneficial treatments. The Spontaneous Urinary Stone Passage ENabled by Drugs (SUSPEND) trial111 was designed to inform the treatment choice. A three-arm RCT was planned to compare tamsulosin and nifedipine with a placebo control to facilitate spontaneous stone passage.
A head-to-head comparison of the two MET agents, nifedipine and tamsulosin, was considered vital. A comparison of the two active arms (combined) with the placebo arm (MET vs. placebo) was also planned, due to uncertainty about the strength of the existing evidence of clinical efficacy. The key outcome of interest was the presence or absence of a stone at 28 days. It was defined as the lack of any further intervention (or planned intervention) to resolve the index ureteric stone.
A review of the evidence base approach was used. Data were available from two systematic reviews125,126 that included RCTs comparing alpha-blockers, calcium channel blockers and a variety of controls (placebo, treatment as usual or prescribed painkillers). 127–129 Only three RCTs compared tamsulosin and nifedipine directly, although there were a number of other trials that compared them to another treatment or a placebo. RCT data from both reviews were combined in a network meta-analysis to maximise the available data to inform the sample size calculation.
The estimated RR effects are shown in Table 3. For simplicity, the uncertainty around the estimates is not shown. The RRs of being stone free, comparing nifedipine and tamsulosin to the mixed control group, were estimated to be 1.50 and 1.70, respectively. Of particular note, the RR of being stone free for tamsulosin compared with nifedipine was estimated to be 1.15.
| RR of treatment A vs. treatment B | Treatment B | |||
|---|---|---|---|---|
| Tamsulosin | Nifedipine | Other | ||
| Treatment A | Tamsulosin | 1.00 | 1.15 | 1.70 |
| Nifedipine | 0.87 | 1.00 | 1.50 | |
| Other | 0.59 | .67 | 1.00 | |
An estimate of the anticipated control (placebo) group event rate for being stone free was needed before the sample size could be calculated. This was estimated to be 50%, using a random effects estimate of the pooled proportion of the control arms of the RCTs from the two systematic reviews. This was then used as the placebo control group response in the sample size calculation, in lieu of better evidence that might be more relevant to the anticipated population. Using this and applying the corresponding RRs from the network meta-analysis, the stone-free level was anticipated to be 75% and 85% in the nifedipine and tamsulosin groups, respectively.
The study sample size was based on the comparison of the nifedipine and tamsulosin treatments. A standard sample size (for a two-sided, 5% significance level and 90% power with a continuity correction) for comparing two proportions gave a required number of 354 in each group. This sample size was inflated to 400 per group to account for an approximate 10% loss to follow-up. The total required sample size was 1200 (applying this size to the placebo group as well).
The placebo control group size was kept at 400 for the planned comparison with any MET (nifedipine and tamsulosin combined), which provided > 90% power. The size of the placebo group could have been reduced using an uneven allocation ratio, but was instead kept an equivalent size to the two active treatment arms. The funding agency strongly supported the inclusion of a placebo arm, given concerns about the potential risk of bias and the relatively small size of the existing placebo-controlled trials. No adjustment was made to the alpha level for multiple treatment comparisons (and therefore no inflation to the standard sample size), as the different comparisons were considered independent research questions: (1) MET compared with placebo control; and (2) nifedipine compated with tamsulosin. See Box 9 for the corresponding sample size explanation from the protocol. 111
Combining the data from the two recent meta-analyses125,126 suggests a RR of approximately 1.50 when comparing MET (either an alpha-blocker or calcium channel blocker) with ‘standard care’ on the primary outcome. These reviews indicate a spontaneous stone passage proportion of approximately 50% in control groups of included RCTs. Only three of the included RCTs directly compared a calcium channel blocker with an alpha-blocker. The RCTs suggested that alpha-blockers are likely to be superior to calcium channel blockers. Combining information from Singh and colleagues126 and Hollingsworth and colleagues125 gives anticipated stone passage of approximately 85% in the alpha-blocker group and approximately 75% in the calcium channel blocker group.
The most conservative sample size is required to detect superiority between the two active treatments and to this end will power the trial. To detect an increase of 10% in the primary outcome (spontaneous stone passage) from 75% in the nifedipine group to 85% in the tamsulosin group, with a two-sided type I error rate of 5% and 90% power, requires 354 per group. Adjusting for 10% loss to follow-up inflates this sample size to 400 per group. No adjustment for multiplicity has been made.
Recruiting 1200 participants (randomising 400 to each of the three treatment groups: tamsulosin, nifedipine or placebo) will provide sufficient power (> 90%) for the MET compared with placebo comparison.
Reproduced from McClinton et al. 111 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. The box includes minor additions and formatting changes to the original text.
Case study 5: the MACRO trial
Chronic rhinosinusitis (CRS) is a common condition, affecting around 10% of the UK adult population, that can lead to chronic respiratory disease or impaired quality of life. Initial management of CRS in the UK is in the family doctor setting, followed by referral to a hospital setting for medical treatment. Initial management fails to deliver sufficient relief for around one in three patients who attend hospital ear, nose and throat clinics. 130,131 The role of antibiotics for CRS is unclear, although they are commonly used in clinical practice. Endoscopic sinus surgery is a commonly conducted operation. Its use varies from centre to centre due to an insufficient evidence base. Two Cochrane systematic reviews132,133 of treatment of CRS with medical and surgical treatments highlighted the need for new randomised trials. Two main research questions related to treatment for patients with CRS were apparent to the investigators:
-
the relative benefits of surgical compared with medical treatment
-
the role of antibiotics.
Given the lack of clarity about current practice in the UK, two possible trial designs were considered potentially appropriate:
-
A two-stage trial incorporating two linked randomised comparisons:
-
stage 1 – antibiotic compared with placebo for 3 months
-
stage 2 – proceeding to receive endoscopic sinus surgery or continued medical therapy for those without significant benefit.
-
-
A three-arm randomised trial comparing antibiotic, placebo and endoscopic sinus surgery.
The relative merits of the study designs are not considered here. Instead, the focus is on specifying the target difference. The Management for Adults with Chronic RhinOsinusitis (MACRO) trial112,113 was designed to have a sample size sufficient for whichever of the two designs was ultimately chosen. An expert panel subsequently choice a variant of the three-arm design.
The primary outcome was the Sinonasal Outcome Test-22 items (SNOT-22), a validated disease-specific quality-of-life instrument. 134 An anchor approach was used to estimate the MID. A ‘medium’ SES (according to Cohen) was also calculated and used, as there is evidence to suggest that 0.5 SDs would be a reasonable estimate of the MID for this type of outcome. 135,136
Data from an existing study were used to infer what might be realistic to observe. 134 Limited work had assessed what would be a MID in the SNOT-22 score. Based on a large existing study of around 2000 patients receiving surgery for CRS with/without nasal polyps, which used the SNOT-22, a SD of 20 seemed plausible (group change score SDs were in the range of 19–20). An analysis adjusting for baseline was planned. A 10-point difference in the SNOT-22 (0.5 SD with SD of 20.0134) could be considered an important difference to detect.
The anchor method study suggested that the MID could be slightly smaller, at 8.9 points. This estimate was derived by calculating the average difference between those who stated post treatment that they were ‘a little better’ (9.5-point reduction) and those who stated they were ‘about the same’ (0.6-point reduction): 9.5 – 0.6 = 8.9 points mean difference. In the aforementioned study134 of surgical patients, the overall mean change score was 16.2, substantially larger than the aforementioned MID estimates. It is not realistic to expect all of this to be observed in a comparison of surgery with another treatment. If 25% (arbitrary, but based on the judgement of the team) of the response were attributed to regression to the mean or the process of receiving treatment of some kind, this would suggest that a difference of 12.2 might be plausible for surgery compared with an essentially non-effective treatment. A similar value for 15% of the effect was also considered (13.8).
The four mean values (8.9, 10.0, 12.2 and 13.8 points) reflected what might be clinically important differences (8.9–10) and realistic target differences (12.2–13.8) to use in the sample size calculations to look at various potential sample sizes under the two designs. A range of standard sample size calculations for a two-arm trial was produced, looking for 80% or 90% statistical power at the two-sided 5% level, using a pooled SD of 20.0 and assuming around 10% missing data (which was plausible based on two previous studies137,138 of patients in this area).
Three-arm design
For 90% power and a 8.9 target difference, 107 per group would be required. Applied to the three-arm design and allowing for 10% missing data, this would lead to 120 per group and 360 overall. In the presence of clustering by surgeon in only the surgery arm, this would still be sufficient to achieve just under 80% power (additionally assuming an ICC of 0.05, 10 clusters of cluster size 12 and similar levels of missing data) for the relevant comparisons. No allowance for unequal cluster sizes was made. However, the actual number of clusters that such a trial would use was thought likely to be somewhat higher, offsetting any potential loss due to uneven cluster sizes.
Two-stage design
What could be achieved with this sample size (360) was then considered for the two-stage design. The full sample would be available for stage 1, barring any missing data. In the absence of clustering, this would be more than sufficient to detect the 8.9-point difference (power of 98%). However, the stage 2 comparison drives the overall sample size calculation in a two-stage design, as the sample size must be inflated to deal with a loss of randomised participants after stage 1. This loss was assumed to be 50%, based on limited prior evidence and erring towards higher estimates. Assuming too low a loss between stages would have a huge impact on the precision of the stage 2 comparison.
An overall sample size of 360 would lead to 180 available at stage 2 (90 per group). Using a target difference of 10.0, a sample size of 360 would achieve 90% power. In the presence of clustering, a large target difference is needed to have 80% or 90% power. The sample size would be sufficient if a target difference of 12.2 was used, after allowing for clustering in the same manner as in the three-arm design. See Box 10 for the corresponding sample size explanation presented in the grant application. The final sample size was inflated at the request of the funder to allow the subgroup with and without nasal polpys to be analysed. For simplicity, this is not considered here.
The trial will recruit 360 patients from 10 UK centres. Sample size justification is based on achieving at least 80% statistical power at the two-sided 5% significance level. No adjustment for multiple comparisons for a two-stage or three-arm design was made as each of the treatment comparisons is distinct. 33
Two-stage designThe MCID in the SNOT-22, based on an anchor study, has been estimated to be 8.9 (SD 20.0). 134 However, previous evidence suggests that an effect size as large as 13.8 for surgery against alternative treatment is plausible. 134 Assuming a more conservative (smaller) difference of 12.2, as both an important and a realistic target difference, and allowing for an ICC of 0.05121 (10 surgeons), leads to a sample size of 80 per group (90 allowing for just over 10% missing data) for stage 2 (surgery vs. ongoing medical treatment) for 90% power and, thus, 180 participants in total. Assuming a 50% non-response rate after the first line of treatment (stage 1) requires doubling the stage 2 number to ensure that sufficient participants progress to stage 2, leading to a size of 360 overall. This size will readily allow (> 95% power) a difference of 8.9 to be detected at stage 1. The assumed non-response rate was based on our recent feasibility study,138 in which symptomatic improvement in the SNOT-22 scores, greater than or equal to the MCID, was seen in 50% of patients at 3 months. If the two-stage design is used, the non-response rate and corresponding numbers progressing through to stage 2 will be assessed in the pilot phase. If necessary, the stage 1 recruitment target will be adjusted.
Three-arm designTo detect the estimated MCID difference (8.9), 107 participants per group are required for 90% power. Allowing for 10% missing data leads to 120 per group (360 overall). Even in the presence of clustering (ICC) of 0.05 with 10 clusters in the surgical arm, the power for this comparison would be around 80%.
The 10% missing data level assumed above for both designs is consistent with the two previous trials of macrolide antibiotics in CRS and our feasibility study. 137,138
Case study 6: the RAPiD trial
Increased use of antibiotics is a major contributor to the spread of antimicrobial resistance. Dentists are responsible for approximately 10% of all antibiotics dispensed in UK community pharmacies. Despite clear clinical guidance, evidence demonstrates that dentists often prescribe antibiotics inappropriately in the absence of clinical need. The effectiveness of strategies to change the behaviour of health professionals is variable, but audit and feedback (A&F) has been shown to lead to small but important improvements in behaviour across a range of contexts and settings. The Reducing Antibiotic Prescribing in Dentistry (RAPiD) trial114 randomised all dental practices with responsibility for prescribing in Scotland (n = 795), using routinely collected Scottish NHS dental prescribing and treatment claim data [available through PRISMS (Prescribing Information System for Scotland)], to compare the effectiveness of different individualised (to dentists with practices) A&F interventions for the translation into practice of national guidance recommendations on antibiotic prescribing.
A total of 795 practices were randomly allocated to an intervention or the control (no A&F). Six hundred and thirty-two intervention group dental practices were subsequently evenly allocated to one of eight A&F groups in a 2 × 2 × 2 factorial design. The three factors were (1) receiving feedback with or without a written behaviour change message, (2) providing the graph of monthly practice prescribing levels with or without health board prescribing levels in the graph and (3) receiving feedback reports twice (0 and 6 months) or three times (0, 6 and 9 months). This led to a total of eight equal-sized intervention groups of 79 practices. The remaining 163 practices in Scotland formed the no intervention control group. The addition of this independent no intervention control group led to a ‘partially’ factorial design rather than fully factorial.
The RAPiD trial sample size calculation was unusual, as the population of sample units was fixed by the size of the country [i.e. every dental practice with responsibility for prescribing (n = 795) in Scotland was expected to take part, as part of a national policy to participate in dental service delivery research]. The sample size calculation was therefore based on identifying whether or not adequate statistical power could be achieved for the primary comparisons for target differences that were considered theoretically plausible (realistic) for a fixed size. The cost implications of a larger sample size were nominal and therefore the full population was always going to be used. The analysis was intended to be at the dentist level, adjusted for dental practice. However, the sample size calculation was carried out at the practice-aggregated level and was therefore conservative.
A systematic review139 demonstrated that the interquartile range of effects of A&F across different settings was 0.5–16%. The study team therefore determined that a 10% reduction (or less) would be both plausible and important. The routine prescribing data indicated that the mean number of antibiotic items prescribed per list was 141.1, with a SD of 140.9. Given that past prescribing behaviour is highly predictive of future prescribing data (correlated) both theoretically and empirically (p = 0.91 observed for the two most recent pre-intervention years), correction for the anticipated baseline correlation was used to reduce the precision. 140 A baseline-prescribing data-adjusted analysis was correspondingly planned.
With the sample size calculation for the A&F comparisons estimated, the study sample size for the comparison of A&F compared with no A&F was fixed by the number of dental practices left in Scotland that could be randomised to no A&F intervention. The detectable difference was 12%, which was still considered both plausible (realistic) and important, should it be observed. Given that the intervention group was being modelled twice within the two main hypotheses (intervention vs. no A&F and intervention factors vs. no intervention factors), Bonferroni’s adjustment was used to adjust the significance level to 2.5%, to maintain an overall two-sided 5% significance level. See Box 11 for the sample size explanation presented in the trial results paper.
The required sample size to achieve 80% power (with two-sided alpha of 2.5%, allowing for the multiple comparisons to allow for the two main research questions) to detect a 10% mean difference in overall antibiotic prescribing between intervention groups was 316 per group. This applied to the comparison between A&F only and A&F with an additional written behaviour change message; between those with and without a health board comparator; and between A&F at 0, 6 and 9 months with 0 and 6 months only. Therefore, 632 practices were required to receive an A&F intervention, with 79 practices in each of the eight sublevel experimental units. There were 795 practices eligible to be included in the trial, which left 163 practices in the control arm. The comparison between the control group (n = 163) and the intervention group (n = 632) had 80% power to detect a 12% mean decrease in overall antibiotic prescribing. The study was not powered to detect realistic two-way interaction effects between behavioural components.
Reproduced from Prior et al. 141 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. The box includes minor additions and formatting changes to the original text.
Chapter 6 Conclusions
Summary
Researchers are faced with a number of decisions when designing a RCT, the most important of which are the choice of trial design, primary outcome and sample size. The last is largely driven by the choice of the target difference for the primary outcome, although other aspects of sample size determination also contribute. It is important to be explicit and transparent about the rationale for and justification of the target difference when undertaking a sample size calculation and subsequently reporting it. The target difference, if well chosen, can be used in the interpretation of the trial results.
The DELTA2 advice and recommendations on specifying a target difference for a RCT has been developed in response to a recognition that there is a need for practical advice to inform its choice. It was developed by a multidisciplinary group and was informed by multiple stages of preliminary work (see Appendix 1 for further details). This new document aims to address this need, and has used real-world case studies to illustrate how the target difference was chosen in clinical trials and to illustrate how the sample size calculation can be reported. It is intended to be of help to individual researchers and accessible to all relevant stakeholder groups. Engagement with funders is planned to maximise the potential value and usefulness to specific stakeholders. For the document to have the most impact, in terms of raising awareness of alternative approaches, the following would be beneficial: encouraging good practice in undertaking and reporting the sample size calculation, and endorsement from journals, funders of randomised trials and relevant professional groups.
Further research priorities
Producing corresponding recommendations for practice and reporting items for atypical sample size calculations, such as those that are simulation based due to their complexity, and studies that utilise an alternative statistical framework (such as Bayesian and/or decision theoretical) are needed to facilitate greater use of these methods.
Developing complementary recommendations for practice and reporting items that extend the work to cover additional alternative trial designs (e.g. multiarm, multistage, umbrella), which have not been explicitly covered.
Acknowledgements
This project was funded by the MRC NIHR Methodology Research Programme in the UK in response to a commissioned call to lead a workshop on this topic in order to produce guidance. The members of the original DELTA2 group were Associate Professor Jonathan Cook, Professor Douglas Altman, Dr Jesse Berlin, Professor Martin Bland, Professor Richard Emsley, Dr Dean Fergusson, Dr Lisa Hampson, Professor Catherine Hewitt, Professor Craig Ramsay, Miss Joanne Rothwell, Dr Robert Smith, Dr William Sones, Professor Luke Vale, Professor Stephen Walters and Professor Steve Julious.
As part of the process of developing this document, a 2-day workshop was held in Oxford in September 2016. The workshop participants were Professor Douglas Altman, Professor David Armstrong, Professor Deborah Ashby, Professor Martin Bland, Dr Andrew Cook, Professor Jonathan Cook, Dr David Crosby, Professor Richard Emsley, Dr Dean Fergusson, Professor Andrew Grieve, Dr Lisa Hampson, Professor Catherine Hewitt, Professor Steve Julious, Professor Graeme MacLennan, Professor Tim Maughan, Professor Jon Nicholl, Dr José Pinheiro, Professor Craig Ramsay, Miss Joanne Rothwell, Dr William Sones, Professor Nigel Stallard, Professor Luke Vale, Professor Stephen Walters and Dr Ed Wilson.
The authors would like to acknowledge and thank the participants in the Delphi exercise and the one-off engagement sessions with various groups, including the SCT, PSI and JSM conference session attendees, along with the other workshop participants who kindly provided helpful input and comments on the scope and content of this document. We would also like to thank, in particular, Dr Robert Smith in his role as a member of the public who provided a helpful public perspective during the workshop and in the development and revision of this document. Finally, the authors would like to thank Stefano Vezzoli for in-depth comments that helped to refine this document, helpful feedback from the MRC Methodological Research Programme Advisory Group, and representatives of the Medicines and Healthcare products Regulatory Agency and Health and Social Care, Northern Ireland.
Dedication
This work is dedicated to Douglas Altman, an inspirational researcher, friend and colleague.
Contributions of authors
Jonathan A Cook (Professor) drafted the initial version of the manuscript, and read and approved the final version.
Steven A Julious (Professor) drafted the initial version of the manuscript, and read and approved the final version.
William Sones (Statistician) contributed to the development of the document, commented on the draft manuscript, and read and approved the final version.
Lisa V Hampson (Associate Director) contributed to the development of the document, commented on the draft manuscript, and read and approved the final version.
Catherine Hewitt (Professor) contributed to the development of the document, commented on the draft manuscript, and read and approved the final version.
Jesse A Berlin (Vice President and Global Head of Epidemiology) contributed to the development of the document, commented on the draft manuscript, and read and approved the final version.
Deborah Ashby (Co-Director) contributed to the development of the document, commented on the draft manuscript, and read and approved the final version.
Richard Emsley (Professor) contributed to the development of the document, commented on the draft manuscript, and read and approved the final version.
Dean A Fergusson (Senior Scientist and Director) contributed to the development of the document, commented on the draft manuscript, and read and approved the final version.
Stephen J Walters (Professor) contributed to the development of the document, commented on the draft manuscript, and read and approved the final version.
Edward CF Wilson (Senior Research Associate in Health Economics) contributed to the development of the document, commented on the draft manuscript, and read and approved the final version.
Graeme MacLennan (Director and Professor) contributed to the development of the document, commented on the draft manuscript, and read and approved the final version.
Nigel Stallard (Professor) contributed to the development of the document, commented on the draft manuscript, and read and approved the final version.
Joanne C Rothwell (PhD student) contributed to the development of the document, commented on the draft manuscript, and read and approved the final version.
Martin Bland (Professor) contributed to the development of the document, commented on the draft manuscript, and read and approved the final version.
Louise Brown (Senior Statistician) contributed to the development of the document, commented on the draft manuscript, and read and approved the final version.
Craig R Ramsay (Director and Professor) contributed to the development of the document, commented on the draft manuscript, and read and approved the final version.
Andrew Cook (Consultant in Public Health Medicine and Fellow in Health Technology Assessment) contributed to the development of the document, commented on the draft manuscript, and read and approved the final version.
David Armstrong (Professor) contributed to the development of the document, commented on the draft manuscript, and read and approved the final version.
Douglas Altman (Professor) contributed to the development of the document, commented on the draft manuscript, and read and approved the final version.
Luke D Vale (Professor) contributed to the development of the document, commented on the draft manuscript, and read and approved the final version.
Publications
Cook JA, Julious SA, Sones W, Rothwell JC, Ramsay CR, Hampson LV, et al. Choosing the target difference (“effect size”) for a randomised controlled trial – DELTA2 guidance protocol. Trials 2017;18:271.
Bell M. New guidance to improve sample size calculations for trials: eliciting the target difference. Trials 2018;19:605.
Cook JA, Julious SA, Sones W, Hampson LV, Hewitt C, Berlin JA, et al. DELTA2 guidance on choosing the target difference and undertaking and reporting the sample size calculation for a randomised controlled trial. BMJ 2018;363:k3750.
Cook JA, Julious SA, Sones W, Hampson LV, Hewitt C, Berlin JA, et al. DELTA2 guidance on choosing the target difference and undertaking and reporting the sample size calculation for a randomised controlled trial. Trials 2018;19:606.
Sones W, Julious SA, Rothwell JC, Ramsay CR, Hampson LV, Emsley R, et al. Choosing the target difference (“effect size”) for a randomised controlled trial – the development of the DELTA2 guidance. Trials 2018;19:542.
Data-sharing statement
All data requests should be submitted to the corresponding author for consideration. Access to anonymised data may be granted following review.
Disclaimers
This report presents independent research funded under a MRC–NIHR partnership. The views and opinions expressed by authors in this publication are those of the authors and do not necessarily reflect those of the NHS, the NIHR, the MRC, NETSCC, the HTA programme or the Department of Health and Social Care. If there are verbatim quotations included in this publication the views and opinions expressed by the interviewees are those of the interviewees and do not necessarily reflect those of the authors, those of the NHS, the NIHR, the MRC, NETSCC, the HTA programme or the Department of Health and Social Care.
References
- Julious S. Sample Sizes for Clinical Trials. Boca Raton, FL: Chapman and Hall/CRC Press; 2010.
- Flight L, Julious SA. Practical guide to sample size calculations: superiority trials. Pharm Stat 2016;15:75-9. https://doi.org/10.1002/pst.1718.
- Flight L, Julious SA. Practical guide to sample size calculations: non-inferiority and equivalence trials. Pharm Stat 2016;15:80-9. https://doi.org/10.1002/pst.1716.
- Julious SA. The ABC of non-inferiority margin setting from indirect comparisons. Pharm Stat 2011;10:448-53. https://doi.org/10.1002/pst.517.
- Lange S, Freitag G. Choice of delta: requirements and reality – results of a systematic review. Biom J 2005;47:12-27. https://doi.org/10.1002/bimj.200410085.
- Committee for Medicinal Products for Human Use . Guideline on the Choice of Non-Inferiority Margin 2005. www.ema.europa.eu/en/documents/scientific-guideline/guideline-choice-non-inferiority-margin_en.pdf (accessed 6 August 2019).
- Weins BL. Choosing an equivalence limit for noninferiority and equivalence trials. Control Clin Trials 2002;23:2-14.
- Jones B, Jarvis P, Lewis JA, Ebbutt AF. Trials to assess equivalence: the importance of rigorous methods. BMJ 1996;313:36-9. https://doi.org/10.1136/bmj.313.7048.36.
- Sones W, Julious SA, Rothwell JC, Ramsay CR, Hampson LV, Emsley R, et al. Choosing the target difference (‘effect size’) for a randomised controlled trial – the development of the DELTA2 guidance. Trials 2018;19. https://doi.org/10.1186/s13063-018-2887-x.
- International Council for Harmonisation . Harmonised tripartite guideline ICH. Statistical principles for clinical trials. International Conference on Harmonisation E9 expert working group. Stat Med 1999;18:1905-42.
- Spiegelhalter DJ, Abrams KR, Myles JP. Bayesian Approaches to Clinical Trials and Health-Care Evaluation. Chicester: John Wiley & Sons; 2004.
- Chuang-Stein C. Sample size and the probability of a successful trial. Pharm Stat 2006;5:305-9. https://doi.org/10.1002/pst.232.
- Charles P, Giraudeau B, Dechartres A, Baron G, Ravaud P. Reporting of sample size calculation in randomised controlled trials: review. BMJ 2009;338. https://doi.org/10.1136/bmj.b1732.
- Cook J, Hislop J, Adewuyi T, Harrild K, Altman D, Ramsay C, et al. Assessing methods to specify the targeted difference for a randomised controlled trial – DELTA (Difference ELicitation in TriAls) review. Health Technol Assess 2014;18. https://doi.org/10.3310/hta18280.
- Hislop J, Adewuyi TE, Vale LD, Harrild K, Fraser C, Gurung T, et al. Methods for specifying the target difference in a randomised controlled trial: the Difference ELicitation in TriAls (DELTA) systematic review. PLOS Med 2014;11. https://doi.org/10.1371/journal.pmed.1001645.
- Cook JA, Hislop JM, Altman DG, Briggs AH, Fayers PM, Norrie JD, et al. Use of methods for specifying the target difference in randomised controlled trial sample size calculations: two surveys of trialists’ practice. Clin Trials 2014;11:300-8. https://doi.org/10.1177/1740774514521907.
- Jaeschke R, Singer J, Guyatt GH. Measurement of health status. Ascertaining the minimal clinically important difference. Control Clin Trials 1989;10:407-15. https://doi.org/10.1016/0197-2456(89)90005-6.
- Hays RD, Woolley JM. The concept of clinically meaningful difference in health-related quality-of-life research. How meaningful is it?. PharmacoEconomics 2000;18:419-23. https://doi.org/10.2165/00019053-200018050-00001.
- Chan KB, Man-Son-Hing M, Molnar FJ, Laupacis A. How well is the clinical importance of study results reported? An assessment of randomized controlled trials. CMAJ 2001;165:1197-202.
- Cook JA, Hislop J, Altman DG, Fayers P, Briggs AH, Ramsay CR, et al. Specifying the target difference in the primary outcome for a randomised controlled trial: guidance for researchers. Trials 2015;16. https://doi.org/10.1186/s13063-014-0526-8.
- Rios LP, Ye C, Thabane L. Association between framing of the research question using the PICOT format and reporting quality of randomized controlled trials. BMC Med Res Methodol 2010;10. https://doi.org/10.1186/1471-2288-10-11.
- Akacha M, Bretz F, Ruberg S. Estimands in clinical trials – broadening the perspective. Stat Med 2017;36:5-19. https://doi.org/10.1002/sim.7033.
- Committee for Human Medicinal Products . ICH E9 (R1) Addendum on Estimands and Sensitivity Analysis in Clinical Trials to the Guideline on Statistical Principles for Clinical Trials 2017. www.ema.europa.eu/en/documents/scientific-guideline/draft-ich-e9-r1-addendum-estimands-sensitivity-analysis-clinical-trials-guideline-statistical_en.pdf (accessed 6 August 2019).
- Leuchs AK, Brandt A, Zinserling J, Benda N. Disentangling estimands and the intention-to-treat principle. Pharm Stat 2017;16:12-9. https://doi.org/10.1002/pst.1791.
- Phillips A, Abellan-Andres J, Soren A, Bretz F, Fletcher C, France L, et al. Estimands: discussion points from the PSI estimands and sensitivity expert group. Pharm Stat 2017;16:6-11. https://doi.org/10.1002/pst.1745.
- Mallinckrodt CH, Lin Q, Lipkovich I, Molenberghs G. A structured approach to choosing estimands and estimators in longitudinal clinical trials. Pharm Stat 2012;11:456-61. https://doi.org/10.1002/pst.1536.
- Billingham SA, Whitehead AL, Julious SA. An audit of sample sizes for pilot and feasibility trials being undertaken in the United Kingdom registered in the United Kingdom Clinical Research Network database. BMC Med Res Methodol 2013;13. https://doi.org/10.1186/1471-2288-13-104.
- National Institute for Health Research . Involve 2017 n.d. www.invo.org.uk/ (accessed 1 April 2019).
- National Institute for Health and Care Excellence . Public Involvement 2017 n.d. www.nice.org.uk/about/nice-communities/public-involvement (accessed 1 April 2019).
- World Medical Association . WMA Declaration of Helsinki – Ethical Principles for Medical Research Involving Human Subjects 2013. www.wma.net/policies-post/wma-declaration-of-helsinki-ethical-principles-for-medical-research-involving-human-subjects/ (accessed 1 April 2019).
- Edwards SJ, Lilford RJ, Braunholtz D, Jackson J. Why ‘underpowered’ trials are not necessarily unethical. Lancet 1997;350:804-7. https://doi.org/10.1016/S0140-6736(97)02290-3.
- Schulz KF, Grimes DA. Sample size calculations in randomised trials: mandatory and mystical. Lancet 2005;365:1348-53. https://doi.org/10.1016/S0140-6736(05)61034-3.
- Cook R, Farewell V. Multiplicity considerations in the design and analysis of clinical trials. J R Stat Soc 1996;159:93-110. https://doi.org/10.2307/2983471.
- Schulz KF, Grimes DA. Multiplicity in randomised trials I: endpoints and treatments. Lancet 2005;365:1591-5. https://doi.org/10.1016/S0140-6736(05)66461-6.
- Kass MA, Heuer DK, Higginbotham EJ, Johnson CA, Keltner JL, Miller JP, et al. The Ocular Hypertension Treatment Study: a randomized trial determines that topical ocular hypotensive medication delays or prevents the onset of primary open-angle glaucoma. Arch Ophthalmol 2002;120:701-13. https://doi.org/10.1001/archopht.120.6.701.
- Burr JM, Botello-Pinzon P, Takwoingi Y, Hernández R, Vazquez-Montes M, Elders A, et al. Surveillance for ocular hypertension: an evidence synthesis and economic evaluation. Health Technol Assess 2012;16. https://doi.org/10.3310/hta16290.
- Sugimoto T, Sozu T, Hamasaki T. A convenient formula for sample size calculations in clinical trials with multiple co-primary continuous endpoints. Pharm Stat 2012;11:118-28. https://doi.org/10.1002/pst.505.
- Walters SJ. Quality of Life Outcomes in Clinical Trials and Health-Care Evaluation: A Practical Guide to Analysis and Interpretation. Chichester: Wiley; 2009.
- Walters SJ. Sample size and power estimation for studies with health related quality of life outcomes: a comparison of four methods using the SF-36. Health Qual Life Outcomes 2004;2. https://doi.org/10.1186/1477-7525-2-26.
- Senn S, Julious S. Measurement in clinical trials: a neglected issue for statisticians?. Stat Med 2009;28:3189-209. https://doi.org/10.1002/sim.3603.
- Wittes J. Commentary on ‘Measurement in clinical trials: a neglected issue for statisticians?’. Stat Med 2009;28:3220-2. https://doi.org/10.1002/sim.3658.
- Sharpe M, Walker J, Holm Hansen C, Martin P, Symeonides S, Gourley C, et al. Integrated collaborative care for comorbid major depression in patients with cancer (SMaRT Oncology-2): a multicentre randomised controlled effectiveness trial. Lancet 2014;384:1099-108. https://doi.org/10.1016/S0140-6736(14)61231-9.
- Hollis S, Campbell F. What is meant by intention to treat analysis? Survey of published randomised controlled trials. BMJ 1999;319:670-4. https://doi.org/10.1136/bmj.319.7211.670.
- Rosenkranz G. Estimands – new statistical principle or the emperor’s new clothes?. Pharm Stat 2017;16:4-5. https://doi.org/10.1002/pst.1792.
- Copay AG, Subach BR, Glassman SD, Polly DW, Schuler TC. Understanding the minimum clinically important difference: a review of concepts and methods. Spine J 2007;7:541-6. https://doi.org/10.1016/j.spinee.2007.01.008.
- Wells G, Beaton D, Shea B, Boers M, Simon L, Strand V, et al. Minimal clinically important differences: review of methods. J Rheumatol 2001;28:406-12.
- Beaton D, Boers M, Wells G. Many faces of the minimal clinically important difference (MICD): a literature review and directions for future research. Curr Opin Rheumatol 2002;14:109-14. https://doi.org/10.1097/00002281-200203000-00006.
- Engel L, Beaton DE, Touma Z. Minimal Clinically Important Difference: A Review of Outcome Measure Score Interpretation. Rheum Dis Clin North Am 2018;44:177-88. https://doi.org/10.1016/j.rdc.2018.01.011.
- Fayers PM, Cuschieri A, Fielding J, Craven J, Uscinska B, Freedman LS. Sample size calculation for clinical trials: the impact of clinician beliefs. Br J Cancer 2000;82:213-19. https://doi.org/10.1054/bjoc.1999.0902.
- Rose G. Sick individuals and sick populations. Int J Epidemiol 2001;30:427-32. https://doi.org/10.1093/ije/30.3.427.
- Kannel WB, Garcia MJ, McNamara PM, Pearson G. Serum lipid precursors of coronary heart disease. Hum Pathol 1971;2:129-51. https://doi.org/10.1016/S0046-8177(71)80023-0.
- Guyatt GH, Osoba D, Wu AW, Wyrwich KW, Norman GR. Clinical Significance Consensus Meeting Group . Methods to explain the clinical significance of health status measures. Mayo Clin Proc 2002;77:371-83. https://doi.org/10.4065/77.4.371.
- de Vet HC, Terluin B, Knol DL, Roorda LD, Mokkink LB, Ostelo RW, et al. Three ways to quantify uncertainty in individually applied ‘minimally important change’ values. J Clin Epidemiol 2010;63:37-45. https://doi.org/10.1016/j.jclinepi.2009.03.011.
- Cella D, Bullinger M, Scott C, Barofsky I. Group vs individual approaches to understanding the clinical significance of differences or changes in quality of life. Mayo Proc 2002;77:384-92. https://doi.org/10.4065/77.4.384.
- Murray DW, MacLennan GS, Breeman S, Dakin HA, Johnston L, Campbell MK, et al. A randomised controlled trial of the clinical effectiveness and cost-effectiveness of different knee prostheses: the Knee Arthroplasty Trial (KAT). Health Technol Assess 2014;18. https://doi.org/10.3310/hta18190.
- Beard DJ, Harris K, Dawson J, Doll H, Murray DW, Carr AJ, et al. Meaningful changes for the Oxford hip and knee scores after joint replacement surgery. J Clin Epidemiol 2015;68:73-9. https://doi.org/10.1016/j.jclinepi.2014.08.009.
- Walters SJ. Consultants’ forum: should post hoc sample size calculations be done?. Pharm Stat 2009;8:163-9. https://doi.org/10.1002/pst.334.
- Julious SA, Walters SJ. Estimating effect sizes for health-related quality of life outcomes. Stat Methods Med Res 2014;23:430-9. https://doi.org/10.1177/0962280213476379.
- Brant R, Sutherland L, Hilsden R. Examining the minimum important difference. Stat Med 1999;18:2593-603. https://doi.org/10.1002/(SICI)1097-0258(19991015)18:19<2593::AID-SIM392>3.0.CO;2-T.
- Whitehead J, Bolland K, Valdès-Márquez E, Lihic A, Ali M, Lees K. Virtual International Stroke Trials Archive Collaborators . Using historical lesion volume data in the design of a new phase II clinical trial in acute stroke. Stroke 2009;40:1347-52. https://doi.org/10.1161/STROKEAHA.108.531442.
- Jacobson NS, Truax P. Clinical significance: a statistical approach to defining meaningful change in psychotherapy research. J Consult Clin Psychol 1991;59:12-9. https://doi.org/10.1037/0022-006X.59.1.12.
- Newnham EA, Harwood KE, Page AC. Evaluating the clinical significance of responses by psychiatric inpatients to the mental health subscales of the SF-36. J Affect Disord 2007;98:91-7. https://doi.org/10.1016/j.jad.2006.07.001.
- Detsky AS. Using cost-effectiveness analysis to improve the efficiency of allocating funds to clinical trials. Stat Med 1990;9:173-84. https://doi.org/10.1002/sim.4780090124.
- Torgerson DJ, Ryan M, Ratcliffe J. Economics in sample size determination for clinical trials. QJM 1995;88:517-21.
- Hollingworth W, McKell-Redwood D, Hampson L, Metcalfe C. Cost-utility analysis conducted alongside randomized controlled trials: are economic end points considered in sample size calculations and does it matter?. Clin Trials 2013;10:43-5. https://doi.org/10.1177/1740774512465358.
- Glick HA. Sample size and power for cost-effectiveness analysis (part 1). PharmacoEconomics 2011;29:189-98. https://doi.org/10.2165/11585070-000000000-00000.
- Glick HA. Sample size and power for cost-effectiveness analysis (Part 2): the effect of maximum willingness to pay. PharmacoEconomics 2011;29:287-96. https://doi.org/10.2165/11585080-000000000-00000.
- National Institute for Health and Care Excellence (NICE) . NICE Process and Methods Guides. Guide to the Methods of Technology Appraisal 2013.
- O’Hagan A. Uncertain Judgements: Eliciting Experts’ Probabilities. Hoboken, NJ: John Wiley & Sons; 2006.
- Gosling JP. Methods for Eliciting Expert Opinion to Inform Health Technology Assessment 2014. https://pdfs.semanticscholar.org/38eb/a762cdaf5d6dae2fee2063bf776d5facec5b.pdf (accessed 6 August 2019).
- Ryan M, Gerard K, Amaya-Amaya M. Using Discrete Choice Experiments to Value Health and Health Care. Dordrecht: Springer; 2008.
- Mt-Isa S, Hallgreen CE, Wang N, Callréus T, Genov G, Hirsch I, et al. Balancing benefit and risk of medicines: a systematic review and classification of available methodologies. Pharmacoepidemiol Drug Saf 2014;23:667-78. https://doi.org/10.1002/pds.3636.
- Barrett B, Brown D, Mundt M, Brown R. Sufficiently important difference: expanding the framework of clinical significance. Med Decis Making 2005;25:250-61. https://doi.org/10.1177/0272989X05276863.
- Bellamy N, Anastassiades TP, Buchanan WW, Davis P, Lee P, McCain GA, et al. Rheumatoid arthritis antirheumatic drug trials. III. Setting the delta for clinical trials of antirheumatic drugs – results of a consensus development (Delphi) exercise. J Rheumatol 1991;18:1908-15.
- Devilee JLA, Knol AB. Software to Support Expert Elicitation. An Exploratory Study of Existing Software Packages 2011. www.rivm.nl/bibliotheek/rapporten/630003001.pdf (accessed 6 August 2019).
- Howard R, Phillips P, Johnson T, O’Brien J, Sheehan B, Lindesay J, et al. Determining the minimum clinically important differences for outcomes in the DOMINO trial. Int J Geriatr Psychiatry 2011;26:812-17. https://doi.org/10.1002/gps.2607.
- Hampson LV, Whitehead J, Eleftheriou D, Tudur-Smith C, Jones R, Jayne D, et al. Elicitation of expert prior opinion: application to the MYPAN trial in childhood polyarteritis nodosa. PLOS ONE 2015;10. https://doi.org/10.1371/journal.pone.0120981.
- Kirkby HM, Wilson S, Calvert M, Draper H. Using e-mail recruitment and an online questionnaire to establish effect size: a worked example. BMC Med Res Methodol 2011;11. https://doi.org/10.1186/1471-2288-11-89.
- Parmar MK, Griffiths GO, Spiegelhalter DJ, Souhami RL, Altman DG, van der Scheuren E. CHART steering committee . Monitoring of large randomised clinical trials: a new approach with Bayesian methods. Lancet 2001;358:375-81. https://doi.org/10.1016/S0140-6736(01)05558-1.
- Parmar MK, Spiegelhalter DJ, Freedman LS. The CHART trials: Bayesian design and monitoring in practice. CHART Steering Committee. Stat Med 1994;13:1297-312. https://doi.org/10.1002/sim.4780131304.
- Chaloner K, Rhame FS. Quantifying and documenting prior beliefs in clinical trials. Stat Med 2001;20:581-600. https://doi.org/10.1002/sim.694.
- Hampson LV, Whitehead J, Eleftheriou D, Brogan P. Bayesian methods for the design and interpretation of clinical trials in very rare diseases. Stat Med 2014;33:4186-201. https://doi.org/10.1002/sim.6225.
- Allison DB, Elobeid MA, Cope MB, Brock DW, Faith MS, Vander Veur S, et al. Sample size in obesity trials: patient perspective versus current practice. Med Decis Making 2010;30:68-75. https://doi.org/10.1177/0272989X09340583.
- Arain M, Campbell MJ, Cooper CL, Lancaster GA. What is a pilot or feasibility study? A review of current practice and editorial policy. BMC Med Res Methodol 2010;10. https://doi.org/10.1186/1471-2288-10-67.
- Kraemer HC, Mintz J, Noda A, Tinklenberg J, Yesavage JA. Caution regarding the use of pilot studies to guide power calculations for study proposals. Arch Gen Psychiatry 2006;63:484-9. https://doi.org/10.1001/archpsyc.63.5.484.
- Cocks K, Torgerson DJ. Sample size calculations for pilot randomized trials: a confidence interval approach. J Clin Epidemiol 2013;66:197-201. https://doi.org/10.1016/j.jclinepi.2012.09.002.
- Teare MD, Dimairo M, Shephard N, Hayman A, Whitehead A, Walters SJ. Sample size requirements to estimate key design parameters from external pilot randomised controlled trials: a simulation study. Trials 2014;15. https://doi.org/10.1186/1745-6215-15-264.
- Whitehead AL, Julious SA, Cooper CL, Campbell MJ. Estimating the sample size for a pilot randomised trial to minimise the overall trial sample size for the external pilot and main trial for a continuous outcome variable. Stat Methods Med Res 2016;25:1057-73. https://doi.org/10.1177/0962280215588241.
- Hippisley-Cox J, Coupland C. Predicting risk of upper gastrointestinal bleed and intracranial bleed with anticoagulants: cohort study to derive and validate the QBleed scores. BMJ 2014;349. https://doi.org/10.1136/bmj.g4606.
- Clarke M, Hopewell S, Chalmers I. Clinical trials should begin and end with systematic reviews of relevant evidence: 12 years and waiting. Lancet 2010;376:20-1. https://doi.org/10.1016/S0140-6736(10)61045-8.
- Sutton AJ, Cooper NJ, Jones DR. Evidence synthesis as the key to more coherent and efficient research. BMC Med Res Methodol 2009;9. https://doi.org/10.1186/1471-2288-9-29.
- Sutton AJ, Higgins JP. Recent developments in meta-analysis. Stat Med 2008;27:625-50. https://doi.org/10.1002/sim.2934.
- Halpern SD, Karlawish JH, Berlin JA. The continuing unethical conduct of underpowered clinical trials. JAMA 2002;288:358-62. https://doi.org/10.1001/jama.288.3.358.
- Cohen J. Statistical Power Analysis for the Behavioral Sciences. New York, NY: Academic Press; 1977.
- Higgins JPT, Green S. Cochrane Handbook for Systematic Reviews of Interventions Version 5.1.0. London: The Cochrane Collaboration; 2011.
- Chinn S. A simple method for converting an odds ratio to effect size for use in meta-analysis. Stat Med 2000;19:3127-31. https://doi.org/10.1002/1097-0258(20001130)19:22<3127::AID-SIM784>3.0.CO;2-M.
- Vist GE, Bryant D, Somerville L, Birminghem T, Oxman AD. Outcomes of patients who participate in randomized controlled trials compared to similar patients receiving similar interventions who do not participate. Cochrane Database Syst Rev 2008;3. https://doi.org/10.1002/14651858.MR000009.pub4.
- Goodman SN, Berlin JA. The use of predicted confidence intervals when planning experiments and the misuse of power when interpreting results. Ann Intern Med 1994;121:200-6. https://doi.org/10.7326/0003-4819-121-3-199408010-00008.
- Schulz KF, Grimes DA. Multiplicity in randomised trials II: subgroup and interim analyses. Lancet 2005;365:1657-61. https://doi.org/10.1016/S0140-6736(05)66516-6.
- Glazener C, Boachie C, Buckley B, Cochran C, Dorey G, Grant A, et al. Urinary incontinence in men after formal one-to-one pelvic-floor muscle training following radical prostatectomy or transurethral resection of the prostate (MAPS): two parallel randomised controlled trials. Lancet 2011;378:328-37. https://doi.org/10.1016/S0140-6736(11)60751-4.
- Hunter KF, Glazener CM, Moore KN. Conservative management for postprostatectomy urinary incontinence. Cochrane Database Syst Rev 2007;2. https://doi.org/10.1002/14651858.CD001843.pub3.
- Lois N, Burr J, Norrie J, Vale L, Cook J, McDonald A, et al. Internal limiting membrane peeling versus no peeling for idiopathic full-thickness macular hole: a pragmatic randomized controlled trial. Invest Ophthalmol Vis Sci 2011;52:1586-92. https://doi.org/10.1167/iovs.10-6287.
- Early Treatment Diabetic Retinopathy Study (ETDRS) Research Group . Early Treatment Diabetic Retinopathy Study design and baseline patient characteristics. ETDRS report number 7. Ophthalmology 1991;98:741-56. https://doi.org/10.1016/S0161-6420(13)38009-9.
- Brooks HL. Macular hole surgery with and without internal limiting membrane peeling. Ophthalmology 2000;107:1939-48. https://doi.org/10.1016/S0161-6420(00)00331-6.
- Paques M, Chastang C, Mathis A, Sahel J, Massin P, Dosquet C, et al. Effect of autologous platelet concentrate in surgery for idiopathic macular hole: results of a multicenter, double-masked, randomized trial. Platelets in Macular Hole Surgery Group. Ophthalmology 1999;106:932-8. https://doi.org/10.1016/S0161-6420(99)00512-6.
- Taggart DP, Lees B, Gray A, Altman DG, Flather M, Channon K. ART Investigators . Protocol for the Arterial Revascularisation Trial (ART). A randomised trial to compare survival following bilateral versus single internal mammary grafting in coronary revascularisation [ISRCTN46552265]. Trials 2006;7. https://doi.org/10.1186/1745-6215-7-7.
- Taggart DP, D’Amico R, Altman DG. Effect of arterial revascularisation on survival: a systematic review of studies comparing bilateral and single internal mammary arteries. Lancet 2001;358:870-5. https://doi.org/10.1016/S0140-6736(01)06069-X.
- Schulz KF, Altman DG, Moher D. CONSORT Group . CONSORT 2010 statement: updated guidelines for reporting parallel group randomised trials. BMJ 2010;340. https://doi.org/10.1136/bmj.c332.
- Chan AW, Tetzlaff JM, Altman DG, Laupacis A, Gøtzsche PC, Krleža-Jerić K, et al. SPIRIT 2013 statement: defining standard protocol items for clinical trials. Ann Intern Med 2013;158:200-7. https://doi.org/10.7326/0003-4819-158-3-201302050-00583.
- Tesfaye S, Coppini D, Bouhassira D, Selvarajah D, Jude E, Rayman G, et al. Optimal Pathway for TreatIng neurOpathic paiN in Diabetes Mellitus (OPTION-DM) Trial. Health Technol Assess 2019. www.journalslibrary.nihr.ac.uk/programmes/hta/153503/#/ (accessed October 2019).
- McClinton S, Starr K, Thomas R, McLennan G, McPherson G, McDonald A, et al. Use of drug therapy in the management of symptomatic ureteric stones in hospitalized adults (SUSPEND), a multicentre, placebo-controlled, randomized trial of a calcium-channel blocker (nifedipine) and an α-blocker (tamsulosin): study protocol for a randomized controlled trial. Trials 2014;15. https://doi.org/10.1186/1745-6215-15-238.
- Blackshaw H, Vennik J, Philpott C, Thomas M, Eyles C, Carpenter J, et al. Expert panel process to optimise the design of a randomised controlled trial in chronic rhinosinusitis (the MACRO programme). Trials 2019;20. https://doi.org/10.1186/s13063-019-3318-3.
- Philpott C, le Conte S, Beard D, Cook J, Sones W, Morris S, et al. Clarithromycin and endoscopic sinus surgery for adults with chronic rhinosinusitis with and without nasal polyps: study protocol for the MACRO randomised controlled trial. Trials 2019;20. https://doi.org/10.1186/s13063-019-3314-7.
- Elouafkaoui P, Young L, Newlands R, Duncan EM, Elders A, Clarkson JE, et al. Translation Research in a Dental Setting (TRiaDS) Research Methodology Group . An audit and feedback intervention for reducing antibiotic prescribing in general dental practice: the RAPiD Cluster Randomised Controlled Trial. PLOS Med 2016;13. https://doi.org/10.1371/journal.pmed.1002115.
- Frobell RB, Roos HP, Roos EM, Roemer FW, Ranstam J, Lohmander LS. Treatment for acute anterior cruciate ligament tear: five year outcome of randomised trial. BMJ 2013;346. https://doi.org/10.1136/bmj.f232.
- Frobell RB, Roos EM, Roos HP, Ranstam J, Lohmander LS. A randomized trial of treatment for acute anterior cruciate ligament tears. N Engl J Med 2010;363:331-42. https://doi.org/10.1056/NEJMoa0907797.
- Roos EM. The 2012 User’s Guide To: Knee Injury and Osteoarthritis Outcome Score KOOS 2012. www.koos.nu/KOOSusersguide2012.pdf (accessed 19 August 2019).
- Roos EM, Lohmander LS. The Knee injury and Osteoarthritis Outcome Score (KOOS): from joint injury to osteoarthritis. Health Qual Life Outcomes 2003;1. https://doi.org/10.1186/1477-7525-1-64.
- Collins NJ, Misra D, Felson DT, Crossley KM, Roos EM. Measures of knee function: International Knee Documentation Committee (IKDC) Subjective Knee Evaluation Form, Knee Injury and Osteoarthritis Outcome Score (KOOS), Knee Injury and Osteoarthritis Outcome Score Physical Function Short Form (KOOS-PS), Knee Outcome Survey Activities of Daily Living Scale (KOS-ADL), Lysholm Knee Scoring Scale, Oxford Knee Score (OKS), Western Ontario and McMaster Universities Osteoarthritis Index (WOMAC), Activity Rating Scale (ARS), and Tegner Activity Score (TAS). Arthritis Care Res 2011;63:208-28. https://doi.org/10.1002/acr.20632.
- Batistatou E, Roberts C, Roberts S. Sample size and power calculations for trials and quasi-experimental studies with clustering. Stata J 2014;14:159-75. https://doi.org/10.1177/1536867X1401400111.
- Cook JA, Bruckner T, MacLennan GS, Seiler CM. Clustering in surgical trials – database of intracluster correlations. Trials 2012;13. https://doi.org/10.1186/1745-6215-13-2.
- Gilron I, Bailey JM, Tu D, Holden RR, Weaver DF, Houlden RL. Morphine, gabapentin, or their combination for neuropathic pain. N Engl J Med 2005;352:1324-34. https://doi.org/10.1056/NEJMoa042580.
- Dworkin RH, Turk DC, Wyrwich KW, Beaton D, Cleeland CS, Farrar JT, et al. Interpreting the clinical importance of treatment outcomes in chronic pain clinical trials: IMMPACT recommendations. J Pain 2008;9:105-21. https://doi.org/10.1016/j.jpain.2007.09.005.
- Julious SA. Sample sizes for clinical trials with normal data. Stat Med 2004;23:1921-86. https://doi.org/10.1002/sim.1783.
- Hollingsworth JM, Rogers MA, Kaufman SR, Bradford TJ, Saint S, Wei JT, et al. Medical therapy to facilitate urinary stone passage: a meta-analysis. Lancet 2006;368:1171-9. https://doi.org/10.1016/S0140-6736(06)69474-9.
- Singh A, Alter HJ, Littlepage A. A systematic review of medical therapy to facilitate passage of ureteral calculi. Ann Emerg Med 2007;50:552-63. https://doi.org/10.1016/j.annemergmed.2007.05.015.
- Taghavi R, Darabi MR, Tavakoli K, Keshvari M. Survey of the effect of tamsulosin and nifedipine on facilitating juxtavesical ureteral stone passage. J Endourol 2005;19.
- Porpiglia F, Ghignone G, Fiori C, Fontana D, Scarpa RM. Nifedipine versus tamsulosin for the management of lower ureteral stones. J Urol 2004;172:568-71. https://doi.org/10.1097/01.ju.0000132390.61756.ff.
- Dellabella M, Milanese G, Muzzonigro G. Randomized trial of the efficacy of tamsulosin, nifedipine and phloroglucinol in medical expulsive therapy for distal ureteral calculi. J Urol 2005;174:167-72. https://doi.org/10.1097/01.ju.0000161600.54732.86.
- Baguley C, Brownlow A, Yeung K, Pratt E, Sacks R, Harvey R. The fate of chronic rhinosinusitis sufferers after maximal medical therapy. Int Forum Allergy Rhinol 2014;4:525-32. https://doi.org/10.1002/alr.21315.
- Young LC, Stow NW, Zhou L, Douglas RG. Efficacy of medical therapy in treatment of chronic rhinosinusitis. Allergy Rhinol 2012;3:e8-e12. https://doi.org/10.2500/ar.2012.3.0027.
- Rimmer J, Fokkens W, Chong LY, Hopkins C. Surgical versus medical interventions for chronic rhinosinusitis with nasal polyps. Cochrane Database Syst Rev 2014;12. https://doi.org/10.1002/14651858.CD006991.pub2.
- Sharma R, Lakhani R, Rimmer J, Hopkins C. Surgical interventions for chronic rhinosinusitis with nasal polyps. Cochrane Database Syst Rev 2014;11. https://doi.org/10.1002/14651858.CD006990.pub2.
- Hopkins C, Gillett S, Slack R, Lund VJ, Browne JP. Psychometric validity of the 22-item Sinonasal Outcome Test. Clin Otolaryngol 2009;34:447-54. https://doi.org/10.1111/j.1749-4486.2009.01995.x.
- Norman GR, Sloan JA, Wyrwich KW. Interpretation of changes in health-related quality of life: the remarkable universality of half a standard deviation. Med Care 2003;41:582-92. https://doi.org/10.1097/01.MLR.0000062554.74615.4C.
- Norman GR, Sloan JA, Wyrwich KW. The truly remarkable universality of half a standard deviation: confirmation through another look. Expert Rev Pharmacoecon Outcomes Res 2004;4:581-5. https://doi.org/10.1586/14737167.4.5.581.
- Erskine SE, Notley C, Wilson AM, Philpott CM. Managing chronic rhinosinusitis and respiratory disease: a qualitative study of triggers and interactions. J Asthma 2015;52:600-5. https://doi.org/10.3109/02770903.2014.995308.
- Bewick JC, Ergo FM, Masterson LM, Philpott CM. Preliminary findings: the feasibility study for a randomized controlled trial of clarithromycin in chronic rhinosinusitis. Otolaryngol Head Neck Surg Endosc 2014;151. https://doi.org/10.1177/0194599814541627a300.
- Ivers N, Jamtvedt G, Flottorp S, Young JM, Odgaard-Jensen J, French SD, et al. Audit and feedback: effects on professional practice and healthcare outcomes. Cochrane Database Syst Rev 2012;6. https://doi.org/10.1002/14651858.CD000259.pub3.
- Borm GF, Fransen J, Lemmens WA. A simple sample size formula for analysis of covariance in randomized clinical trials. J Clin Epidemiol 2007;60:1234-8. https://doi.org/10.1016/j.jclinepi.2007.02.006.
- Prior M, Elouafkaoui P, Elders A, Young L, Duncan EM, Newlands R, et al. Evaluating an audit and feedback intervention for reducing antibiotic prescribing behaviour in general dental practice (the RAPiD trial): a partial factorial cluster randomised trial protocol. Implement Sci 2014;9. https://doi.org/10.1186/1748-5908-9-50.
- Hedayat AS, Wang J, Xu T. Minimum clinically important difference in medical studies. Biometrics 2015;71:33-41. https://doi.org/10.1111/biom.12251.
- Rouquette A, Blanchin M, Sébille V, Guillemin F, Côté SM, Falissard B, et al. The minimal clinically important difference determined using item response theory models: an attempt to solve the issue of the association with baseline score. J Clin Epidemiol 2014;67:433-40. https://doi.org/10.1016/j.jclinepi.2013.10.009.
- Zhang Y, Zhang S, Thabane L, Furukawa TA, Johnston BC, Guyatt GH. Although not consistently superior, the absolute approach to framing the minimally important difference has advantages over the relative approach. J Clin Epidemiol 2015;68:888-94. https://doi.org/10.1016/j.jclinepi.2015.02.017.
- Chen MH, Willan AR. Determining optimal sample sizes for multistage adaptive randomized clinical trials from an industry perspective using value of information methods. Clin Trials 2013;10:54-62. https://doi.org/10.1177/1740774512467404.
- Andronis L, Barton PM. Adjusting estimates of the expected value of information for implementation: theoretical framework and practical application. Med Decis Making 2016;36:296-307. https://doi.org/10.1177/0272989X15614814.
- Breeze P, Brennan A. Valuing trial designs from a pharmaceutical perspective using value-based pricing. Health Econ 2015;24:1468-82. https://doi.org/10.1002/hec.3103.
- Hall PS, Edlin R, Kharroubi S, Gregory W, McCabe C. Expected net present value of sample information: from burden to investment. Med Decis Making 2012;32:E11-21. https://doi.org/10.1177/0272989X12443010.
- Jalal H, Goldhaber-Fiebert JD, Kuntz KM. Computing expected value of partial sample information from probabilistic sensitivity analysis using linear regression metamodeling. Med Decis Making 2015;35:584-95. https://doi.org/10.1177/0272989X15578125.
- Madan J, Ades AE, Price M, Maitland K, Jemutai J, Revill P, et al. Strategies for efficient computation of the expected value of partial perfect information. Med Decis Making 2014;34:327-42. https://doi.org/10.1177/0272989X13514774.
- Maroufy V, Marriott P, Pezeshk H. An optimization approach to calculating sample sizes with binary responses. J Biopharm Stat 2014;24:715-31. https://doi.org/10.1080/10543406.2014.902851.
- McKenna C, Claxton K. Addressing adoption and research design decisions simultaneously: the role of value of sample information analysis. Med Decis Making 2011;31:853-65. https://doi.org/10.1177/0272989X11399921.
- Menzies NA. An efficient estimator for the expected value of sample information. Med Decis Making 2016;36:308-20. https://doi.org/10.1177/0272989X15583495.
- Sadatsafavi M, Marra C, Bryan S. Two-level resampling as a novel method for the calculation of the expected value of sample information in economic trials. Health Econ 2013;22:877-82. https://doi.org/10.1002/hec.2869.
- Steuten L, van de Wetering G, Groothuis-Oudshoorn K, Retèl V. A systematic and critical review of the evolving methods and applications of value of information in academia and practice. PharmacoEconomics 2013;31:25-48. https://doi.org/10.1007/s40273-012-0008-3.
- Strong M, Oakley JE, Brennan A. Estimating multiparameter partial expected value of perfect information from a probabilistic sensitivity analysis sample: a nonparametric regression approach. Med Decis Making 2014;34:311-26. https://doi.org/10.1177/0272989X13505910.
- Welton NJ, Madan JJ, Caldwell DM, Peters TJ, Ades AE. Expected value of sample information for multi-arm cluster randomized trials with binary outcomes. Med Decis Making 2014;34:352-65. https://doi.org/10.1177/0272989X13501229.
- Welton NJ, Soares MO, Palmer S, Ades AE, Harrison D, Shankar-Hari M, et al. Accounting for heterogeneity in relative treatment effects for use in cost-effectiveness models and value-of-information analyses. Med Decis Making 2015;35:608-21. https://doi.org/10.1177/0272989X15570113.
- Willan AR, Eckermann S. Value of information and pricing new healthcare interventions. PharmacoEconomics 2012;30:447-59. https://doi.org/10.2165/11592250-000000000-00000.
- Willan AR, Eckermann S. Accounting for between-study variation in incremental net benefit in value of information methodology. Health Econ 2012;21:1183-95. https://doi.org/10.1002/hec.1781.
- Ross S, Milne J, Dwinnell S, Tang S, Wood S. Is it possible to estimate the minimal clinically important treatment effect needed to change practice in preterm birth prevention? Results of an obstetrician survey used to support the design of a trial. BMC Med Res Methodol 2012;12. https://doi.org/10.1186/1471-2288-12-31.
- Chen H, Zhang N, Lu X, Chen S. Caution regarding the choice of standard deviations to guide sample size calculations in clinical trials. Clin Trials 2013;10:522-9. https://doi.org/10.1177/1740774513490250.
- Fay MP. An alternative property for evaluating sample size for normal data using preliminary data. Clin Trials 2013;10:990-1. https://doi.org/10.1177/1740774513506965.
- Kirby S, Burke J, Chuang-Stein C, Sin C. Discounting phase 2 results when planning phase 3 clinical trials. Pharm Stat 2012;11:373-85. https://doi.org/10.1002/pst.1521.
- Sim J, Lewis M. The size of a pilot study for a clinical trial should be calculated in relation to considerations of precision and efficiency. J Clin Epidemiol 2012;65:301-8. https://doi.org/10.1016/j.jclinepi.2011.07.011.
- Valentine JC, Aloe AM. How to communicate effect sizes for continuous outcomes: a review of existing options and introducing a new metric. J Clin Epidemiol 2016;72:84-9. https://doi.org/10.1016/j.jclinepi.2015.10.017.
- Willan AR. Sample size determination for cost-effectiveness trials. PharmacoEconomics 2011;29:933-49. https://doi.org/10.2165/11587130-000000000-00000.
- Wilson EC. A practical guide to value of information analysis. PharmacoEconomics 2015;33:105-21. https://doi.org/10.1007/s40273-014-0219-x.
- Ferreira ML, Herbert RD, Ferreira PH, Latimer J, Ostelo RW, Nascimento DP, et al. A critical review of methods used to determine the smallest worthwhile effect of interventions for low back pain. J Clin Epidemiol 2012;65:253-61. https://doi.org/10.1016/j.jclinepi.2011.06.018.
- Pezold ML, Pusic AL, Cohen WA, Hollenberg JP, Butt Z, Flum DR, et al. Defining a research agenda for patient-reported outcomes in surgery: using a delphi survey of stakeholders. JAMA Surg 2016;151:930-6. https://doi.org/10.1001/jamasurg.2016.1640.
- Williamson PR, Altman DG, Blazeby JM, Clarke M, Devane D, Gargon E, et al. Developing core outcome sets for clinical trials: issues to consider. Trials 2012;13. https://doi.org/10.1186/1745-6215-13-132.
- Senn S. Statistical Issues in Drug Development. Chichester: John Wiley & Sons; 2007.
- Senn S. Controversies concerning randomization and additivity in clinical trials. Stat Med 2004;23:3729-53. https://doi.org/10.1002/sim.2074.
- Machin D. Sample Size Tables for Clinical Studies. Chichester: Wiley-Blackwell; 2009.
- Chuang-Stein C, Kirby S, Hirsch I, Atkinson G. The role of the minimum clinically important difference and its impact on designing a trial. Pharm Stat 2011;10:250-6. https://doi.org/10.1002/pst.459.
- Carroll KJ. Back to basics: explaining sample size in outcome trials, are statisticians doing a thorough job?. Pharm Stat 2009;8:333-45. https://doi.org/10.1002/pst.362.
- Royston P, Barthel FM, Parmar MK, Choodari-Oskooei B, Isham V. Designs for clinical trials with time-to-event outcomes based on stopping guidelines for lack of benefit. Trials 2011;12. https://doi.org/10.1186/1745-6215-12-81.
- Bland JM. The tyranny of power: is there a better way to calculate sample size?. BMJ 2009;339. https://doi.org/10.1136/bmj.b3985.
- Bacchetti P. Current sample size conventions: flaws, harms, and alternatives. BMC Med 2010;8. https://doi.org/10.1186/1741-7015-8-17.
- Amrhein V, Greenland S, McShane B. Scientists rise up against statistical significance. Nature 2019;567:305-7. https://doi.org/10.1038/d41586-019-00857-9.
- Copsey B, Thompson JY, Vadher K, Ali U, Dutton SJ, Fitzpatrick R, et al. Sample size calculations are poorly conducted and reported in many randomized trials of hip and knee osteoarthritis: results of a systematic review. J Clin Epidemiol 2018;104:52-61. https://doi.org/10.1016/j.jclinepi.2018.08.013.
- Proschan MA. Sample size re-estimation in clinical trials. Biom J 2009;51:348-57. https://doi.org/10.1002/bimj.200800266.
- Bauer P, Koenig F. The reassessment of trial perspectives from interim data – a critical view. Stat Med 2006;25:23-36. https://doi.org/10.1002/sim.2180.
- Dallow N, Fina P. The perils with the misuse of predictive power. Pharm Stat 2011;10:311-17. https://doi.org/10.1002/pst.467.
- Kent DM, Trikalinos TA, Hill MD. Are unadjusted analyses of clinical trials inappropriately biased toward the null?. Stroke 2009;40:672-3. https://doi.org/10.1161/STROKEAHA.108.532051.
- Flight L, Julious SA. Practical guide to sample size calculations: an introduction. Pharm Stat 2016;15:68-74. https://doi.org/10.1002/pst.1709.
- Schulz KF, Grimes DA. Sample size slippages in randomised trials: exclusions and the lost and wayward. Lancet 2002;359:781-5. https://doi.org/10.1016/S0140-6736(02)07882-0.
- Curran D, Sylvester RJ, Hoctin Boes G. Sample size estimation in phase III cancer clinical trials. Eur J Surg Oncol 1999;25:244-50. https://doi.org/10.1053/ejso.1998.0635.
- Ford I, Norrie J. The role of covariates in estimating treatment effects and risk in long-term clinical trials. Stat Med 2002;21:2899-908. https://doi.org/10.1002/sim.1294.
- Pokhrel A, Dyba T, Hakulinen T. A Greenwood formula for standard error of the age-standardised relative survival ratio. Eur J Cancer 2008;44:441-7. https://doi.org/10.1016/j.ejca.2007.10.026.
- Royston P, Parmar MK. An approach to trial design and analysis in the era of non-proportional hazards of the treatment effect. Trials 2014;15. https://doi.org/10.1186/1745-6215-15-314.
- White IR. Uses and limitations of randomization-based efficacy estimators. Stat Methods Med Res 2005;14:327-47. https://doi.org/10.1191/0962280205sm406oa.
- Wittes J. Sample size calculations for randomized controlled trials. Epidemiol Rev 2002;24:39-53. https://doi.org/10.1093/epirev/24.1.39.
- Emsley R, Dunn G, White IR. Mediation and moderation of treatment effects in randomised controlled trials of complex interventions. Stat Methods Med Res 2010;19:237-70. https://doi.org/10.1177/0962280209105014.
- Dunn G, Maracy M, Tomenson B. Estimating treatment effects from randomized clinical trials with noncompliance and loss to follow-up: the role of instrumental variable methods. Stat Methods Med Res 2005;14:369-95. https://doi.org/10.1191/0962280205sm403oa.
- Dunn G, Emsley R, Liu H, Landau S, Green J, White I, et al. Evaluation and validation of social and psychological markers in randomised trials of complex interventions in mental health: a methodological research programme. Health Technol Assess 2015;19. https://doi.org/10.3310/hta19930.
- Cesana BM, Antonelli P. Sample size calculations in clinical research should also be based on ethical principles. Trials 2016;17. https://doi.org/10.1186/s13063-016-1277-5.
- Jain A, Sierakowski A, Gardiner MD, Beard D, Cook J, Cooper C, et al. Nail bed INJury Assessment Pilot (NINJA-P) study: should the nail plate be replaced or discarded after nail bed repair in children? Study protocol for a pilot randomised controlled trial. Pilot Feasibility Stud 2015;1. https://doi.org/10.1186/s40814-015-0025-z.
- Thabane L, Ma J, Chu R, Cheng J, Ismaila A, Rios LP, et al. A tutorial on pilot studies: the what, why and how. BMC Med Res Methodol 2010;10. https://doi.org/10.1186/1471-2288-10-1.
- Browne RH. On the use of a pilot sample for sample size determination. Stat Med 1995;14:1933-40. https://doi.org/10.1002/sim.4780141709.
- Bonati LH, Dobson J, Featherstone RL, Ederle J, van der Worp HB, de Borst GJ, et al. Long-term outcomes after stenting versus endarterectomy for treatment of symptomatic carotid stenosis: the International Carotid Stenting Study (ICSS) randomised trial. Lancet 2015;385:529-38. https://doi.org/10.1016/S0140-6736(14)61184-3.
- Gillett R. An average power criterion for sample size estimation. J R Stat Soc Ser D 1994;43:389-94. https://doi.org/10.2307/2348574.
- Gordon Lan KK, Wittes JT. Some thoughts on sample size: a Bayesian-frequentist hybrid approach. Clin Trials 2012;9:561-9. https://doi.org/10.1177/1740774512453784.
- Neuenschwander B, Capkun-Niggli G, Branson M, Spiegelhalter DJ. Summarizing historical information on controls in clinical trials. Clin Trials 2010;7:5-18. https://doi.org/10.1177/1740774509356002.
- Schmidli H, Gsteiger S, Roychoudhury S, O’Hagan A, Spiegelhalter D, Neuenschwander B. Robust meta-analytic-predictive priors in clinical trials with historical control information. Biometrics 2014;70:1023-32. https://doi.org/10.1111/biom.12242.
- Burke DL, Billingham LJ, Girling AJ, Riley RD. Meta-analysis of randomized phase II trials to inform subsequent phase III decisions. Trials 2014;15. https://doi.org/10.1186/1745-6215-15-346.
- Brown BW, Herson J, Atkinson EN, Rozell ME. Projection from previous studies: a Bayesian and frequentist compromise. Control Clin Trials 1987;8:29-44. https://doi.org/10.1016/0197-2456(87)90023-7.
- Ciarleglio MM, Arendt CD, Peduzzi PN. Selection of the effect size for sample size determination for a continuous response in a superiority clinical trial using a hybrid classical and Bayesian procedure. Clin Trials 2016;13:275-85. https://doi.org/10.1177/1740774516628825.
- Eaton ML, Murihead RJ, Soita SI. On the limiting behaviour of the ‘probability of claiming superiority’ in a Bayesian context. Bayesian Anal 2013;8:221-32. https://doi.org/10.1214/13-BA809.
- Whitehead J, Valdés-Márquez E, Johnson P, Graham G. Bayesian sample size for exploratory clinical trials incorporating historical data. Stat Med 2008;27:2307-27. https://doi.org/10.1002/sim.3140.
- Joseph L, Belisle P. Bayesian sample size determination for normal means and differences between normal means. J R Stat Soc Ser D 1997;46:209-26. https://doi.org/10.1111/1467-9884.00077.
- Pezeshk H, Nematollahi N, Maroufy V, Gittins J. The choice of sample size: a mixed Bayesian/ frequentist approach. Stat Methods Med Res 2009;18:183-94. https://doi.org/10.1177/0962280208089298.
- Stallard N, Miller F, Day S, Hee SW, Madan J, Zohar S, et al. Determination of the optimal sample size for a clinical trial accounting for the population size. Biom J 2017;59:609-25. https://doi.org/10.1002/bimj.201500228.
- Claxton K. The irrelevance of inference: a decision-making approach to the stochastic evaluation of health care technologies. J Health Econ 1999;18:341-64. https://doi.org/10.1016/S0167-6296(98)00039-3.
- Eckermann S, Willan AR. Expected value of sample information with imperfect implementation: improving practice and reducing uncertainty with appropriate counterfactual consideration. Med Decis Making 2016;36:282-3. https://doi.org/10.1177/0272989X16635130.
- Zhu H, Zhang S, Ahn C. Sample size considerations for split-mouth design. Stat Methods Med Res 2017;26:2543-51. https://doi.org/10.1177/0962280215601137.
- Barker D, McElduff P, D’Este C, Campbell MJ. Stepped wedge cluster randomised trials: a review of the statistical methodology used and available. BMC Med Res Methodol 2016;16. https://doi.org/10.1186/s12874-016-0176-5.
- Kuijper B, Tans JT, Beelen A, Nollet F, de Visser M. Cervical collar or physiotherapy versus wait and see policy for recent onset cervical radiculopathy: randomised trial. BMJ 2009;339. https://doi.org/10.1136/bmj.b3883.
- Julious SA, Machin D, Tan SB. An Introduction to Statistics in Early Phase Trials. Oxford: Wiley-Blackwell; 2010.
- Julious SA, McIntyre NE. Sample sizes for trials involving multiple correlated must-win comparisons. Pharm Stat 2012;11:177-85. https://doi.org/10.1002/pst.515.
- Fernandes N, Stone A. Multiplicity adjustments in trials with two correlated comparisons of interest. Stat Methods Med Res 2011;20:579-94. https://doi.org/10.1177/0962280210378943.
- Kerry SM, Bland JM. Sample size in cluster randomisation. BMJ 1998;316. https://doi.org/10.1136/bmj.316.7130.549.
- Donner A, Klar N. Design and Analysis of Cluster Randomization Trials in Health Research. London: Arnold; 2000.
- Ukoumunne OC, Gulliford MC, Chinn S, Sterne JA, Burney PG. Methods for evaluating area-wide and organisation-based interventions in health and health care: a systematic review. Health Technol Assess 1999;3. https://doi.org/10.3310/hta3050.
- Campbell MK, Fayers PM, Grimshaw JM. Determinants of the intracluster correlation coefficient in cluster randomized trials: the case of implementation research. Clin Trials 2005;2:99-107. https://doi.org/10.1191/1740774505cn071oa.
- Eldridge SM, Ashby D, Kerry S. Sample size for cluster randomized trials: effect of coefficient of variation of cluster size and analysis method. Int J Epidemiol 2006;35:1292-300. https://doi.org/10.1093/ije/dyl129.
- Rutterford C, Copas A, Eldridge S. Methods for sample size determination in cluster randomized trials. Int J Epidemiol 2015;44:1051-67. https://doi.org/10.1093/ije/dyv113.
- Roberts C, Roberts SA. Design and analysis of clinical trials with clustering effects due to treatment. Clin Trials 2005;2:152-62. https://doi.org/10.1191/1740774505cn076oa.
- Senn S. Cross-Over Trials in Clinical Research. Chichester: Wiley; 2002.
- Brookes ST, Whitely E, Egger M, Smith GD, Mulheran PA, Peters TJ. Subgroup analyses in randomized trials: risks of subgroup-specific analyses; power and sample size for the interaction test. J Clin Epidemiol 2004;57:229-36. https://doi.org/10.1016/j.jclinepi.2003.08.009.
- Chen DT, Huang PY, Lin HY, Haura EB, Antonia SJ, Cress WD, et al. Strategies for power calculations in predictive biomarker studies in survival data. Oncotarget 2016;7:80373-81. https://doi.org/10.18632/oncotarget.12124.
- Gönen M. Planning for subgroup analysis: a case study of treatment-marker interaction in metastatic colorectal cancer. Control Clin Trials 2003;24:355-63. https://doi.org/10.1016/S0197-2456(03)00006-0.
- Mackey HM, Bengtsson T. Sample size and threshold estimation for clinical trials with predictive biomarkers. Contemp Clin Trials 2013;36:664-72. https://doi.org/10.1016/j.cct.2013.09.005.
- Kairalla JA, Coffey CS, Thomann MA, Muller KE. Adaptive trial designs: a review of barriers and opportunities. Trials 2012;13. https://doi.org/10.1186/1745-6215-13-145.
- Wassmer G, Brannath W. Group Sequential and Confirmatory Adaptive Designs in Clinical Trials. Berlin: Springer; 2016.
- Sydes MR, Parmar MK, James ND, Clarke NW, Dearnaley DP, Mason MD, et al. Issues in applying multi-arm multi-stage methodology to a clinical trial in prostate cancer: the MRC STAMPEDE trial. Trials 2009;10. https://doi.org/10.1186/1745-6215-10-39.
- Wason JM, Jaki T. Optimal design of multi-arm multi-stage trials. Stat Med 2012;31:4269-79. https://doi.org/10.1002/sim.5513.
Appendix 1 Development of the DELTA2 advice and recommendations
Synopsis
The details of the development of the DELTA2 advice and recommendations have been reported elsewhere and are reproduced here. Methods and findings of stages 1–5 of the project, along with associated discussion, are given below.
Methodology of the literature reviews, Delphi study, consensus meeting, stakeholder engagement and finalisation of advice and recommendations
A summary of the methods used in each stage is given below.
Stages 1 and 2: identifying relevant literature and eliciting expert opinion
Literature search
A systematic review was performed to identify recent publications detailing novel approaches to determining the target difference for a RCT. Publications were identified using a systematic search within the PubMed database for articles published after the DELTA review (1 January 2011–31 March 2016). 14,15 The search was restricted to journals in which previous relevant methodological work in this area had been published,14,15 supplemented by other leading journals in epidemiology, health economics, health research methodology, statistics and trials. Full details of the search strategy used can be found in Appendix 2.
In addition to the systematic review of publications, a review of existing online guidance provided by funding schemes and advisory bodies was performed.
Search for guidance
Guidance documents prepared by trial funding and advisory bodies to assist applicants applying for funding for a RCT were inspected for relevant text. Searches were carried out for documents associated with UK trial-funding schemes, run by NIHR, including Efficacy and Mechanism Evaluation, Health Technology Assessment, the Research for Patient Benefit programme, Programme Grants for Applied Research, Public Health Research, Invention for Innovation, Health Services and Delivery Research, the MRC Developmental Pathway Funding Scheme, Arthritis Research UK (now known as Versus Arthritis), the British Heart Foundation, Cancer Research UK (CRUK) (Phase III clinical trial, new agent, population research) and the Wellcome Trust (Health Challenge Innovation Fund). The UK Health Research Authority’s documentation was searched. A search of guidance documents provided by the NIHR Research Design Service (RDS) was also performed. Similar searches were performed for leading international funding streams and regulatory agencies [Agency for Healthcare Research and Quality, Canadian Institutes of Health Research, European Commission Horizon 2020, Food and Drug Administration, Health Canada, National Health and Medical Research Council, National Institutes of Health (NIH) and Patient-Centered Outcomes Research Institute]. Information contained within guidance for applicants applying for trial funding from funders and research advisory bodies regarding the choice of target difference was extracted.
Inclusion and exclusion criteria
The title and abstract of articles identified within the PubMed database search were independently assessed by two reviewers to identify publications worthy of further assessment. The full text of a publication deemed worthy of further assessment was then analysed by a reviewer and included if considered to report a development not already encompassed within the previous DELTA review. 14,15
Data extraction
Publications viewed to be of relevance were reviewed by an expert reviewer and aspects of interest noted. Information on undertaking a sample size calculation and the target difference choice was identified within the websites of trial funding and advisory bodies, and the content assessed by two reviewers. A third (content expert) member of the team acted as arbiter for all disagreements or when further content expertise was required.
Stage 3: Delphi study
A multiround Delphi study was conducted with stakeholders known to have an interest in the design of RCTs. Participants were asked about what guidance was needed on specifying the target difference in a RCT sample size calculation. A 2-day consensus meeting and a one-off stakeholder engagement session was embedded within the Delphi study (stage 4; see Stage 4: 2-day consensus meeting and one-off stakeholder engagement sessions for details). Findings from the first Delphi round were considered by the 2-day consensus meeting to aid construction of a draft DELTA2 advice and recommendations document. A second-round questionnaire was sent with a hyperlink to the draft document. Views and comments on the draft document overall, the main body of the document, case studies, appendices and references were requested. Rounds 1 and 2 questionnaires are available on request from the corresponding author. A group of known methods experts, the inclusion of which was informed by the DELTA review and findings from stage 1, alongside representatives of key trial groups, were invited to participate in the Delphi study. Representatives for groups, including the UK Clinical Research Collaboration network of CTUs, the MRC Hubs for Trials Methodology Research (HTMR), NIHR/MRC/CRUK funding programme panels, the NIHR statistics group and the NIHR RDS were contacted, using publicly available contact information, and invited to participate.
Participants comprised one named individual per group (unit, board, MRC HTMR, RDS centre or programme, e.g. the director, chairperson or senior methodologist). These groups represent UK centres and networks of excellence that undertake high-quality trials research. As of 1 July 2016, there were 48 (fully or provisionally) registered CTUs, five MRC HTMR and the 10 regions in the NIHR RDS in England and the Research Design and Conduct Service in Wales. Based on the premise that a minimum of 30 participants would be required to participate in the Delphi process, and assuming one-third of invitees would agree to participate, it was felt that at least 90 invitations needed to be made. Owing to the arbitrary nature of this target, no strict maximum was applied and 162 invitations were made.
Stage 4: 2-day consensus meeting and one-off stakeholder engagement sessions
2-day consensus meeting
Proposals about the structure and content of the output document, put forward as part of the first-round Delphi process, in addition to literature developments and existing guidance practices, were presented to 25 stakeholders in a face-to-face, 2-day meeting. Additionally, a number of participants gave presentations that provided an overview of the use of specific approaches and/or personal experience of working in this area. Stakeholders, selected to cover a range of perspectives, areas of expertise and roles within RCT design, discussed and refined the proposal for the output document and reached a consensus on the format of the draft advice and recommendations document.
One-off stakeholder engagement sessions
To gain a broader range of opinions, engagement sessions were held at the SCT 37th annual meeting on 17 May 2016, the PSI conference on 16 May 2017 and at the JSM conference on 1 August 2017. Participants were invited to provide views on the scope and structure of the guidance needed, and to offer constructive feedback on the draft guidance.
Stage 5: finalisation of advice and recommendations documentation
The provisional advice and recommendations were drafted on completion of stages 1–4 and circulated among the DELTA2 members and Delphi participants for comments. UK funder representatives will be asked to assess the advice and recommendations to ensure that the document meets funding panel requirements and allow implementation of changes required for specific forms of publication.
Results
Stage 1: systematic literature search
The search identified 1395 potentially relevant reports (Figure 2). Following the screening of titles and abstracts, 73 publications were full-text assessed. Of these, 28 were included in the review as representing a development of one of the previously identified seven broad method types (Table 4 and see Appendix 2). Minor developments were identified for the health economic (including cost–utility and value of information), opinion-seeking, pilot/preliminary study and SES approaches. No new methods were identified. Most developments (17 articles) related to the use of variants of the value of information approach. A number of helpful review articles that summarise different methods and variations in application were identified; these covered willingness to pay66,67 and value of information167,168 health economic-based approaches, and estimation of the smallest worthwhile difference formulation of a MCID, which covered anchor, distribution, opinion-seeking and SES methods. 169 Identified articles on relevant topics (e.g. that address statistical aspects of sample size calculations or an existing method, but contain no new development) were considered as potential references in this document, irrespective of whether or not they were included in this review.
FIGURE 2.
Flow diagram.
| Study | Year | Journal | Method | Methodological development |
|---|---|---|---|---|
| Hedayat et al.142 | 2015 | Biometrics | Anchor | Variation in threshold-based approach to estimating the MID |
| Rouquette et al.143 | 2014 | Journal of Clinical Epidemiology | Anchor | Use of item response model approach to calculate MCID estimate from anchor assessment |
| Zhang et al.144 | 2015 | Journal of Clinical Epidemiology | Anchor | Assessment of expressing MID as absolute and relative difference |
| Hollingworth et al.65 | 2013 | Clinical Trials | HE (cost–utility) | Assessment of cost–utility-based sample size approaches |
| Chen and Willan145 | 2013 | Clinical Trials | HE (VOI) | VOI for multistage adaptive trials from industry perspective |
| Andronis and Barton146 | 2016 | Medical Decision Making | HE (VOI) | Expected value of sample information variant estimator |
| Breeze and Brennan147 | 2015 | Health Economics | HE (VOI) | ENBS from pharmaceutical perspective using value-based pricing |
| Hall et al.148 | 2012 | Medical Decision Making | HE (VOI) | Expected net present value of sample information approach |
| Jalal et al.149 | 2015 | Medical Decision Making | HE (VOI) | Meta modelling approach to calculating the expected value of sample information |
| Madan et al.150 | 2014 | Medical Decision Making | HE (VOI) | Efficient approach to calculating the expected value of partial perfect information (applicable to calculating the expected value of sample information) |
| Maroufy et al.151 | 2014 | Journal of Biopharmaceutical Statistics | HE (VOI) | Method for calculating expected net gain of sampling |
| McKenna and Claxton152 | 2011 | Medical Decision Making | HE (VOI) | Exploration of the role of value of sample information analysis |
| Menzies153 | 2016 | Medical Decision making | HE (VOI) | Expected value of sampling information estimator |
| Sadatsafavi et al.154 | 2013 | Health Economics | HE (VOI) | Expected value of sample information variant estimator |
| Steuten et al.155 | 2013 | PharmacoEconomics | HE (VOI) | Comprehensive review of VOI methodological developments |
| Strong et al.156 | 2014 | Medical Decision Making | HE (VOI) | Meta-modelling approach to calculating the expected value of sample information |
| Welton et al.157 | 2014 | Medical Decision Making | HE (VOI) | Application of expected value of sampling information to a cluster trial |
| Welton et al.158 | 2015 | Medical Decision Making | HE (VOI) | ENBS accounting for heterogeneity in treatment effects |
| Willan and Eckermann159 | 2012 | PharmacoEconomics | HE (VOI) | Framework for exploring the perspective of societal decision-maker and industry |
| Willan and Eckermann160 | 2012 | Health Economics | HE (VOI) | Accounting for between-study variation in value of information approach |
| Kirkby et al.78 | 2011 | BMC Medical Research Methodology | Opinion-seeking | Survey approach to estimate MCID in trial setting |
| Ross et al.161 | 2012 | BMC Medical Research Methodology | Opinion-seeking | Survey approach to estimate MCID with three treatment options |
| Chen et al.162 | 2013 | Clinical Trials | Pilot/preliminary study | Comparison of approaches to using SDs from preliminary study (e.g. pilot or Phase II study) |
| Fay163 | 2013 | Clinical Trials | Pilot/preliminary study | Variation in approach to using SDs from preliminary study (e.g. pilot or Phase II study) |
| Kirby et al.164 | 2012 | Pharmaceutical Statistics | Pilot/preliminary study | Variation in approaches to discounting evidence from preliminary study |
| Sim and Lewis165 | 2012 | Journal of Clinical Epidemiology | Pilot/preliminary study | Inflation factor for pilot study SD estimate for use in trial sample size calculation |
| Whitehead et al.88 | 2016 | Statistics Method in Medical Research | Pilot/preliminary study | Assessment of size of pilot study needed to inform main trial |
| Valentine and Aloe166 | 2016 | Journal of Clinical Epidemiology | SES | Alternative effect size metric proposed |
Stage 2: search for guidance
A search for guidance documentation on the websites for the 15 trial-funding and advisory bodies listed within Search for guidance was performed (see also Appendix 2). On the majority of websites, trial design guidance emphasised the need for applicants to provide sufficient detail to justify the chosen sample size, often going on to discuss techniques employed to calculate sample size, but without providing any details or guidance on how this should be done. In particular, there was little specific guidance provided to assist researchers in specifying the target difference. The use of pilot/preliminary studies and ‘interim data’ was noted with limited further comment.
Stage 3: Delphi study
Invitations to participate in the Delphi study were sent (by e-mail on 29 July 2016) to 58 methods experts, along with 104 named representatives of key trial groups (including the UK Clinical Research Collaboration network of CTUs, the MRC HTMR, NIHR/MRC/CRUK funding programme panels, the NIHR statistics group and the NIHR RDS). Of the 162 individuals invited to participate, responses were received from 84 (52%), of whom 78 (48%) accepted the invitation and six formally declined to participate. Acceptance of the invitation was allowed up to 10 October 2016 (the last acceptance was received on 4 October 2016).
The round 1 questionnaire was open for completion between 11 August and 10 October 2016. Of the 78 experts and representatives who agreed to participate, 69 (88%) completed the round 1 questionnaire once invited by e-mail, whereas nine did not complete it. The demographics of those who ultimately participated in the Delphi study are given in Table 5. Participants represented a range of RCT roles, with design, analysis and evaluating funding proposals well represented. The majority of participants (57 of the 69 who completed round 1; 83%) were primarily affiliated with an academic institution and the majority of participants were from the UK (55 of the 69 who completed round 1; 80%). Views on whether or not specific topics and alternative designs (i.e. not a ‘standard’ two-arm, parallel-group design) should be covered within the output document are given in Figures 3 and 4. Delphi participants showed strongest support (≥ 25%) for extensive coverage on alternative research questions and handling multiple primary outcomes. Across most topics there was 50–70% support for proportionate coverage, except for mechanistic studies and public and patient perspectives on the choice of the target difference. Regarding alternative study designs, the strongest support for extensive coverage was for adaptive designs, cluster randomised trials and multiarm trials (all > 25%). Across all designs there was 50–60% support for proportionate coverage.
| Question | Response | Count (percentage of participants) |
|---|---|---|
| Your role in RCTs (select all that apply) | Involved in analysis of RCTs | 42 (61) |
| Involved in RCT design (collaborating clinician) | 7 (10) | |
| Involved in RCT design (lead/chief investigator) | 23 (33) | |
| Involved in RCT design (statistician/methodologist) | 49 (71) | |
| Other (please specify) | 16 (23) | |
| Serves on a funding panel/board which evaluates applications for RCT funding | 43 (62) | |
| Primary RCT-related affiliation | Academic institution | 57 (83) |
| Contract research organisation | 2 (3) | |
| Funder of RCTs (e.g. NIHR in the UK or NIH in the USA) | 5 (7) | |
| Health-care provider (e.g. NHS in the UK) | 3 (4) | |
| Pharmaceutical/medical device company | 2 (3) | |
| Where do you work? If you work across Europe or internationally, please choose the category in which the majority of your work is performed | Canada | 3 (4) |
| Ireland | 1 (1) | |
| Other European country | 1 (1) | |
| UK | 55 (80) | |
| USA | 9 (13) | |
| Australasia | 0 (0) | |
| Other | 0 (0) |
FIGURE 3.
Round 1 Delphi online questionnaire responses: specific topics to address within target difference recommendations.
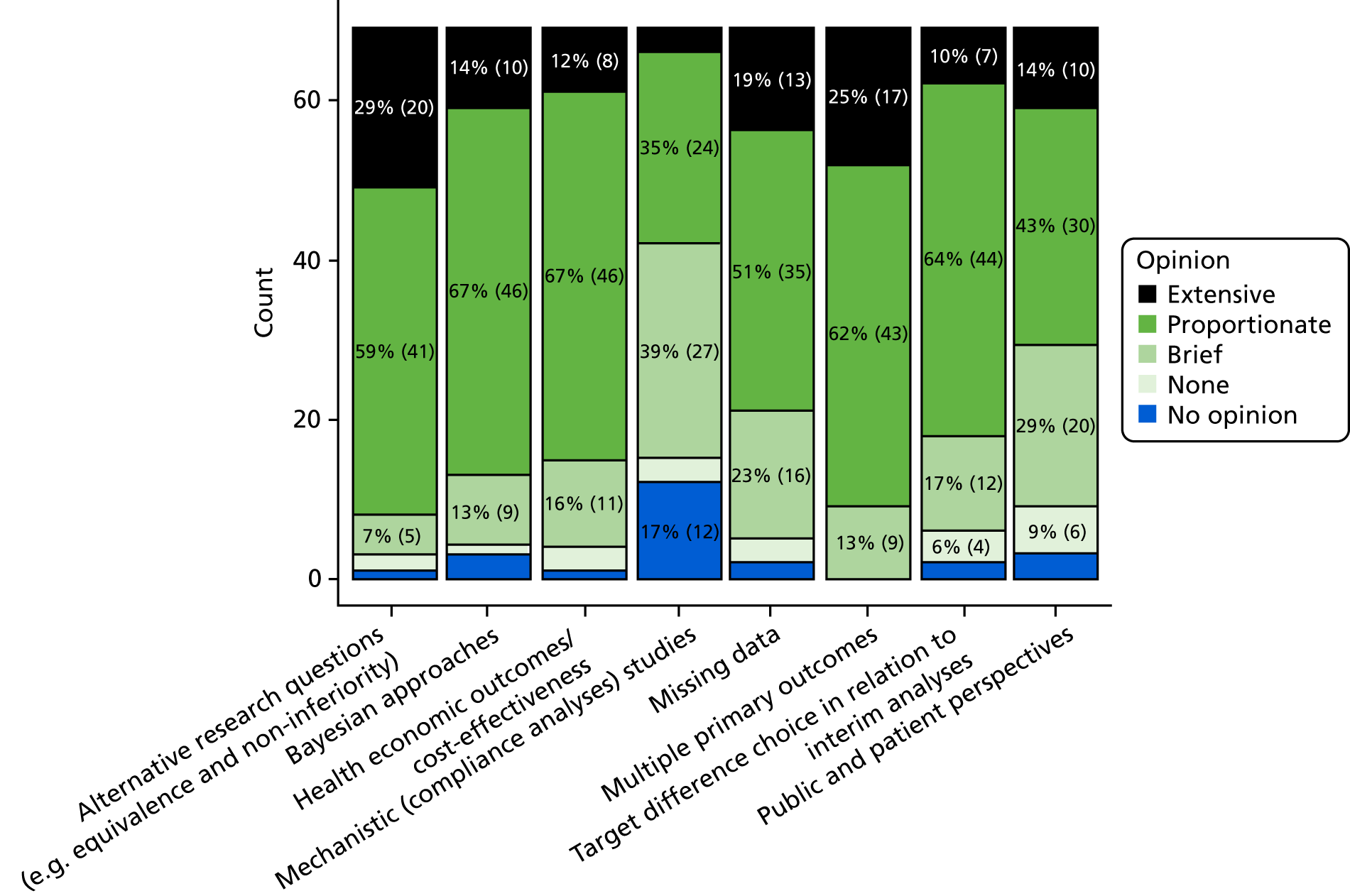
FIGURE 4.
Round 1 Delphi online questionnaire responses: alternative trial designs to address within target difference advice and recommendations.
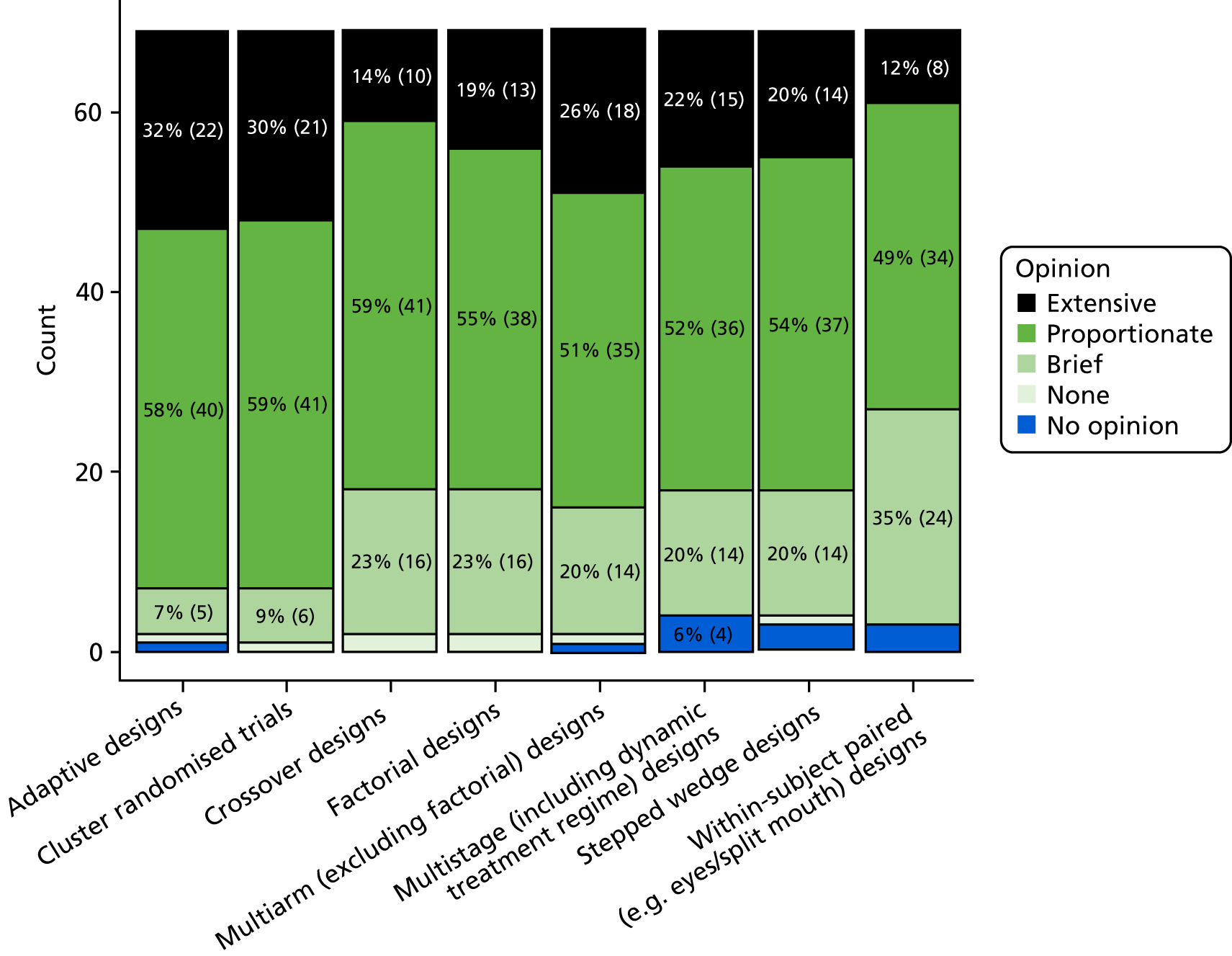
A total of 56 free-text comments were made, covering personal views on specific topics, views on the framing of research questions, and the audience that should be targeted for the advice and recommendations. Comments also included suggestions for additional trial designs to cover references and case study topics. The round 2 questionnaire was open for completion between 1 September and 12 November 2017. Only participants who completed round 1 were invited to participate in round 2, in which assessment of draft guidelines was required. Only two rounds were performed to fit with the project timescale and progress. Of the 69 participants invited to participate in round 2, 38 (55%) completed round 2. Findings from the round 2 questionnaire are summarised in Figure 5. Over 80% either ‘somewhat’ or ‘strongly’ agreed that the document was useful overall for the recommendations, case studies and appendices; 21 suggestions for improving the main text were made (11 regarding the case studies and nine on the appendices). In round 2, 62 free-text comments were provided, which, again, covered a range of suggestions for improving the main text, adding an executive summary, improving the signposting of sections, incorporating views on the case studies and appendices, additional references, raising the issues of estimands and personal views on various topics. Comments made in round 1 and 2 questionnaires, along with feedback from stage 4, led to a substantial number of changes to the document prior to its finalisation. The most substantive being incorporating an executive summary and increasing the number of case studies.
FIGURE 5.
Round 2 Delphi online questionnaire responses.
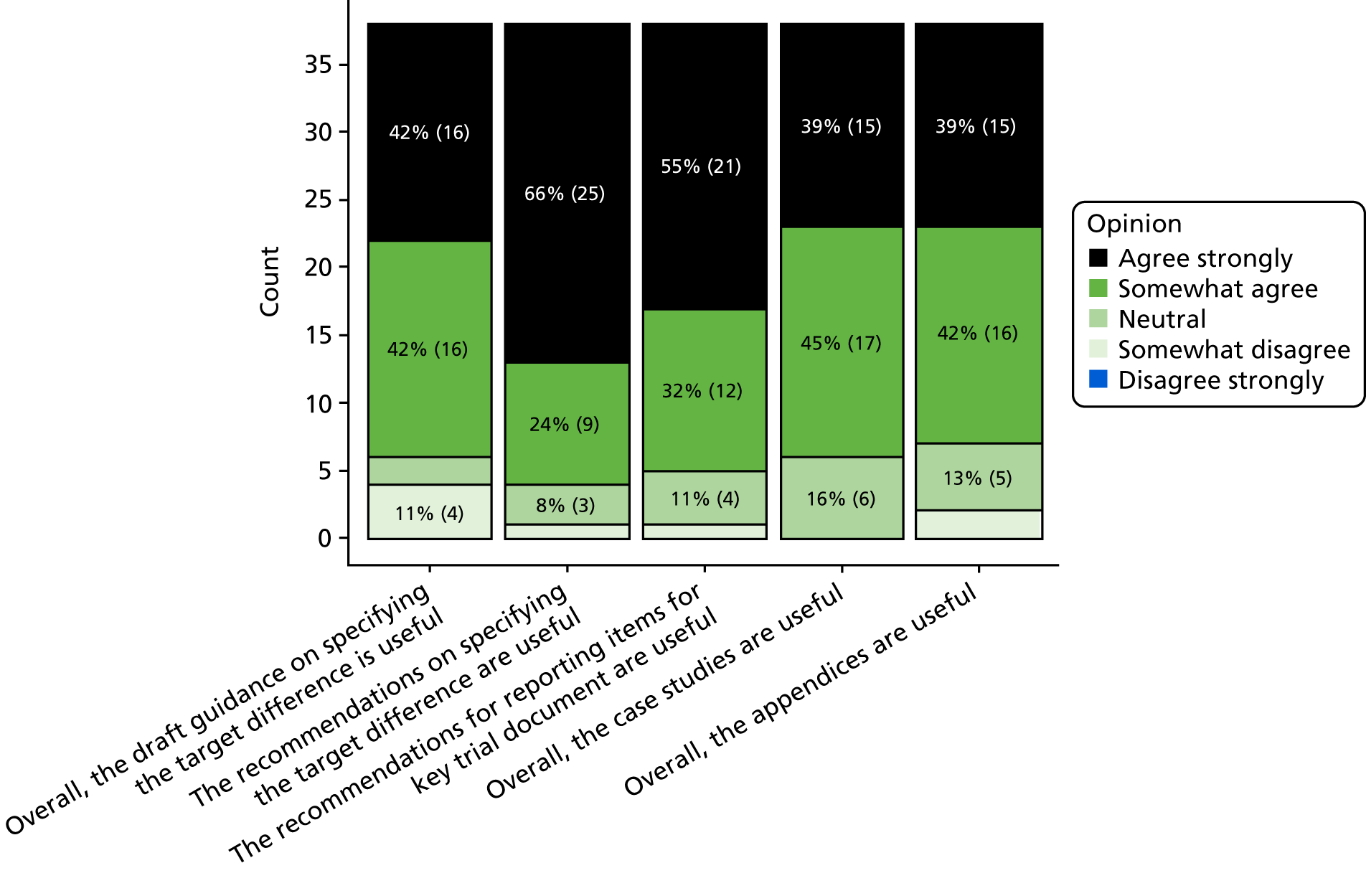
Stage 4: 2-day meeting and stakeholder engagement
An engagement session was held at the SCT in May 2016, when the project was introduced, and views on the scope and broad content of the output document were invited through audience participation. Following this, a 2-day workshop was held in Oxford on 27 and 28 September 2016, which involved 25 participants, including CTU directors, study investigators, project funder representatives, funding panel members, researchers with experts in sample size methods, senior trial statisticians and PPI representatives. The workshop included presentations of the findings from the initial two stages of the project, the SCT engagement session and round 1 of the Delphi study, and focused on decisions relating to the scope and content of the output document. An initial structure for the first draft of the document was developed in the light of the findings from the round 1 questionnaire available at the time of the meeting.
A revised structure was agreed by participants at the workshop. Drafting of individual sections was allocated to individuals. The recommendations on conducting a sample size calculation were initially drafted. The various sections were then developed into the first full draft of the document; this was circulated to all of the DELTA2 project group for comment, with the draft revised in the light of these. An iterative process of comments and revisions was followed until the final version was agreed.
Subsequently, two further engagement sessions were held at PSI and JSM conferences. At the time of the session, the most current draft of the document was made available to participants. Both within- and post-meeting feedback highlighted the need to consider the role of estimands and the minimum (statistically) detectable difference in the sample size calculation, leading to revisions in the document. There was broad consensus, although not universal agreement, on the need for advice and recommendations and the main topics it needed to cover from stakeholders across the various meetings and from the Delphi study. Differences of opinion tended to be about which topics needed to be covered and how important it was that they were covered.
Stage 5: finalisation, adaptation and dissemination
The draft advice and recommendations were reviewed by the representatives of the project’s funders (MRC NIHR Methodology Advisory Group) on 2 October 2017. A number of revisions were made in the light of feedback received from the advisory group and further feedback from the authors. The revised text of the main documentation was finalised on 28 February 2018. It was endorsed by the MRC NIHR Methodology Advisory Group on 12 March 2018, with minor updating of references, and the final version was produced on 18 April 2018. Engagement with individual funders and funding programmes about the best way to utilise the document and adapt to their needs is ongoing. Journals could refer to this document and the reporting recommendations in the guidance for authors. Potentially, the CONSORT statement could be extended to incorporate more specific information on the sample size calculation, as detailed in the DELTA2 recommendations for reporting.
Discussion
Overview
The target difference is arguably the key value in a conventional sample size calculation, but also the most difficult to choose. The DELTA2 project sought to produce more detailed advice and recommendations for researchers and funder representatives, to aid researchers in making this choice and funder representatives in assessing the choice made. Building on the DELTA guidance,14,20 a number of aspects were explored through engagement with stakeholders and the findings are summarised in this paper.
Decisions on scope and content
As part of the process, we explored uncertainty about what methods for sample size determination should be covered. In particular, the views on two methods (value of information and SES-based approaches), which were included in the DELTA guidance,14,20 were debated and the inclusion reconsidered. There was general agreement that they should be included again, but, in particular, the distinctive nature of the value of information approach required greater prominence. The need for some consideration of alternative statistical approaches (aside from the specification of the target difference per se) was also relatively strong. This resulted in specific appendices and boxes within the main text covering more common alternative statistical methods and trial designs, and dealing with related aspects such as compliance analyses and missing data.
The need for more practical advice and recommendations was raised multiple times in various responses and in the engagement sessions. This led to two main additions in the final document. First, 10 recommendations were made for specifying the target difference and a list of corresponding reporting items was included for instances when the conventional sample size approach is used. It is hoped that this will go some way to support researchers and funders undertaking and assessing sample size calculations. It is recognised that future adaptation to accommodate other study designs and statistical approaches will be needed. Second, a number of case studies were included, reflecting different trial designs and covering different conditions. Additional case studies could be added over time to provide a more complete coverage of the range of trial designs, statistical approaches and methods for specifying the target difference.
Overall, the DELTA2 advice and recommendations are more comprehensive than the original DELTA guidance (and also more detailed, with over 25,000 words, compared with around 4000 words). It covers a much broader range of trials and approaches, with more practical advice and recommendations about how to undertake a sample size calculation for a RCT. A number of areas for further research were identified. Addressing these evidence gaps would help inform advice and recommendations for less common statistical approaches and trial designs.
Strength and limitations
The main strength of this advice and recommendation lies in the extensive preparatory work undertaken in both the DELTA2 project and also the original DELTA work. The multiple avenues for engagement with stakeholders represent another strength, as this provided opportunities to solicit views on relevant topics and feedback on the draft document from various stakeholders. A variety of methods were used to inform the development of the document, including systematic reviews of the literature, a Delphi study using online questionnaires, engagement sessions with stakeholder groups and a 2-day workshop.
Participants in the various stages of the project were self-selected and may not be fully representative of all stakeholders. In particular, despite several attempts, there was limited involvement of industry statisticians, with the exception of the PSI stakeholder meeting, and participants were mostly academic statisticians. Overall, those involved were possibly more methodologically interested than those who did not engage. Timings of key meetings meant that flexibility was needed in the conduct of the stages and they were not carried out in a sequential manner, as originally envisaged.
The Delphi study had only 69 participants and had only two rounds, with a substantial drop off between rounds 1 and 2. Unlike other implementations of a Delphi study, a scoring system was not used to rank topics,170 nor was a formalised definition of consensus171 used, as reflected in the more informal determination of consensus in this application.
The scope of some of the stages was purposely limited due to time and resource constraints. The journals searched for methodological developments were those thought to be most likely to publish new developments. It is possible that other developments have been published in other journals, which would have potentially been missed. Consulted stakeholders were predominantly based in the UK and the engagement sessions were limited in number and dependent on acceptance of the proposal at the respective stakeholder meetings.
Appendix 2 Development of the DELTA2 advice and recommendations: supporting material
Search strategy details
Search terms used were sample size or target difference or effect size or important difference or detectable difference or power calculation or value of information or value of perfect information or value of partial perfect information or value of sampling information or expected net gain.
The period searched was 1 January 2011 to 31 March 2016.
A search was performed of the articles from the following journals for relevant publications:
American Journal of Public Health, Biometrical Journal, Biometrics, Biometrika, Biostatistics, BMC Medical Research Methodology, Clinical Trials, Contemporary Clinical Trials, Health Economics, International Journal of Epidemiology, Journal of Biopharmaceutical Statistics, Journal of Public Health Medicine, Journal of Clinical Epidemiology, Medical Decision Making, Pharmaceutical Statistics, PharmacoEconomics, Public Health, Statistics in Biopharmaceutical Research, Statistics in Medicine, Statistical Methods in Medical Research, Trials and Value in Health.
List of included studies
For a list of included studies see Appendix 1, Table 4.
Findings from the review of relevant guidance
The findings from the review of relevant guidance is summarised in Table 6.
| Organisation | Source | Summary/excerpt |
|---|---|---|
| British Heart Foundation | URL: www.bhf.org.uk/-/media/files/research/clinical-study-guidelines_interventional-study-(1).pdf?la=en (accessed 20 April 2018) | Clinical study guidelines:Proposed sample size. Specify the number of participants and centres (including both control and treatment groups)Power calculations. Give details of the estimated effect size, power and/or precision employed in the calculation. Justify the estimated effect size and the assumptions underlying the sample size calculations |
| Health Research Authority | URL: www.hra.nhs.uk/documents/2014/05/guidance-questions-considerations-clinical-trials.pdf (accessed 20 April 2018) | If researchers are too optimistic about the size of the expected treatment difference, the sample size will be too small, and the study may not have sufficient power to detect the minimum clinically important difference – in which case it will be inconclusive |
| MRC | URL: www.mrc.ac.uk/documents/pdf/complex-interventions-guidance/ (accessed 20 April 2018) | Generic:For small studies, which may not produce statistically significant results if the initial assumptions about effect sizes, recruitment rates, etc., were over-optimistic, pooling makes the results far more usefulLicensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License2019The authorshttps://creativecommons.org/licenses/by-nc-sa/4.0/Pilot/preliminary study:The feasibility and piloting stage includes testing procedures for their acceptability, estimating the likely rates of recruitment and retention of subjects, and the calculation of appropriate sample sizes ..... Pilot study results should be interpreted cautiously when making assumptions about the required sample size, likely response rates, etc., when the evaluation is scaled up. Effects may be smaller or more variable and response rates lower when the intervention is rolled out across a wider range of settingsLicensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License2019The authorshttps://creativecommons.org/licenses/by-nc-sa/4.0/ |
| RDS | URL: www.rds-london.nihr.ac.uk/resources/statistics/ (accessed 20 April 2018) | Justifying the number of participants – or the ‘sample size’ – is a vital part of planning a clinical trial for ethical reasonsIn order to work out the sample size to achieve given power, you need to know several things, including what your outcome measure is, and how big the improvement in this outcome has to be to be considered clinically important. The latter is a clinical issue, not a statistical one, and as an expert in your field you will be in a better position to answer this than a statistician |
| CRUK | URL: www.cancerresearchuk.org/sites/default/files/egms_guidelines_-_prc_grant_applications_0.pdf (accessed 20 April 2018) | For each research question to be answered state the statistical analysis to be used, name the variables and describe the values. State the numbers of samples to be included in each analysis. Describe what can be achieved with this number of samples, including as appropriate the associated level of statistical power and be transparent about any potential limitations. Clarify other relevant details, either actual or expected, such as prevalence rates for biomarkers, numbers of events in clinical outcomes and length of follow-up for clinical outcomes. For research proposals using non-standard or non-well-known measures, a full copy of each measure must be included within an appendix to the application |
| Wellcome Trust | URL: www.wellcome.ac.uk/Funding/Innovations/Awards/Health-Innovation-Challenge-Fund/index.htm (accessed 20 April 2018) | All proposals submitted to the Health Innovation Challenge Fund must satisfy the following criteria:Projects must have already demonstrated ‘proof-of-principle’ supported by experimental and, where feasible, in vivo data. Evidence from the applicant’s team must clearly illustrate the technical feasibility of the project and demonstrate the potential for development from its current state to a product approved for use in humans. Early stage research or discovery science is not fundableProposals must include first testing in man during the concluding stages of the project and must have the potential to benefit patients within the following 3–5 years, having demonstrated efficacy and received the necessary regulatory approvals© The Wellcome Trust (www.wellcome.ac.uk) and is licensed under Creative Commons Attribution 2.0 UK2019© The Wellcome Trusthttps://creativecommons.org/licenses/by/2.0/uk/ |
| NIHR | URL: www.hra.nhs.uk/resources/before-you-apply/clinical-study-design-considerations/ (accessed 20 April 2018) | Refers to Health Research Authority guidance |
| Food and Drug Administration | URLs: www.fda.gov/RegulatoryInformation/Guidances/ucm126501.htm; www.accessdata.fda.gov/scripts/cdrh/cfdocs/cfCFR/CFRSearch.cfm?fr=314.126 (accessed 20 April 2018) | The study uses a design that permits a valid comparison with a control to provide a quantitative assessment of drug effect. The protocol for the study and report of results should describe the study design precisely; for example, duration of treatment periods, whether treatments are parallel, sequential, or crossover, and whether the sample size is predetermined or based upon some interim analysis |
| Health Canada | URL: www.hc-sc.gc.ca/dhp-mps/prodpharma/applic-demande/guide-ld/ich/efficac/e6-eng.php (accessed 20 April 2018) | The number of subjects planned to be enrolled. In multicentre trials, the numbers of enrolled subjects projected for each trial site should be specified. Reason for choice of sample size, including reflections on (or calculations of) the power of the trial and clinical justificationRefers to ICH harmonised tripartite guideline structure and content of clinical study reports:Using the usual method for determining the appropriate sample size, the following items should be specified: a primary variable, the test statistic, the null hypothesis, the alternative (‘working’) hypothesis at the chosen dose(s) (embodying consideration of the treatment difference to be detected or rejected at the dose and in the subject population selected), the probability of erroneously rejecting the null hypothesis (the type I error), and the probability of erroneously failing to reject the null hypothesis (the type II error), as well as the approach to dealing with treatment withdrawals and protocol violationsThe size of a trial is influenced by the disease to be investigated, the objective of the study and the study endpoints. Statistical assessments of sample size should be based on the expected magnitude of the treatment effect, the variability of the data, the specified (small) probability of error (see ICH E9) and the desire for information or subsets of the population or secondary endpoints |
| European Commission Horizon 2020 |
http://ec.europa.eu/health/human-use/clinical-trials/directive/index_en.htm (accessed 20 April 2018) http://ec.europa.eu/health/files/eudralex/vol-1/reg_2014_536/reg_2014_536_en.pdf (accessed 20 April 2018) |
. . . a description of the statistical methods to be employed, including, if relevant:– timing of any planned interim analysis and the number of subjects planned to be enrolled;– reasons for choice of sample sizeThe members of the International Conference on Harmonisation of Technical Requirements for Registration of Pharmaceuticals for Human Use (ICH) have agreed on a detailed set of guidelines on good clinical practice which is an internationally accepted standard for designing, conducting, recording and reporting clinical trials, consistent with principles that have their origin in the World Medical Association’s Declaration of Helsinki. When designing, conducting, recording and reporting clinical trials, detailed questions may arise as to the appropriate quality standard. In such a case, the ICH guidelines on good clinical practice should be taken appropriately into account for the application of the rules set out in this Regulation, provided that there is no other specific guidance issued by the Commission and that those guidelines are compatible with this RegulationLicensed under the Creative Commons Attribution 4.0 International (CC BY 4.0) licence. The Commission’s reuse policy is implemented by the Commission Decision of 12 December 2011 on the reuse of Commission documents2019The authorshttps://creativecommons.org/licenses/by/4.0/ |
| NIHR Statistics Group | URL: https://statistics-group.nihr.ac.uk/ (accessed 20 April 2018) | No specific relevant guidance |
| Canadian Institutes of Health Research | URL: www.cihr-irsc.gc.ca/e/193.html (accessed 20 April 2018) | No specific relevant guidance |
| PCORI |
URL: www.pcori.org/research-results/research-methodology/pcori-methodology-standards (accessed 20 April 2018) URL: www.pcori.org/funding-opportunities/how-apply/have-question/chronic-low-back-pain-pfa-applicant-faqs (accessed 20 April 2018) |
RC-3: Power and sample size estimates must use appropriate methods to account for the dependence of observations within clusters and the degrees of freedom available at the cluster level. The methods used to reflect dependence should be clearly described. Sources should be provided for the methods and for the data used to estimate the degree of dependence. Sensitivity analyses incorporating different degrees of dependence must be reported. For simpler designs, the dependence in the data can be reflected in the intraclass correlation. Dependence can also be reflected in variance components. Other factors that affect the power calculation and should be described include the design of the study, the magnitude of the hypothesized intervention effect, the prespecified primary analysis, and the desired type I error ratePCORI does not require a minimum project sample size, as this will be up to the investigative team and will vary depending on the specific project. However, as noted in the PFA, ‘The studies must be relatively large, in part to be able to demonstrate differences in comparative effectiveness in the study arms as randomized, but also to allow adequate power to detect the potential differences in treatment responses in patient subgroups.’ We note that estimating sample size sufficient to provide adequate power for subgroup analysis can be challenging and typically requires expert consultation. Other potential challenges to achieving target sample size (e.g., unintended crossover) should also be factored into sample size considerations as appropriate |
| NIH | URL: www.nimh.nih.gov/research-priorities/policies/enhancing-the-reliability-of-nimh-supported-research-through-rigorous-study-design-and-reporting.shtml (accessed 20 April 2018) | Generic:Justification of sample size, including power calculations, number of subjects per condition, and a clear definition of ‘a subject’ (e.g., in electrophysiological studies, is ‘one subject’ the recording from one cell or the recording from one animal?) |
| National Health and Medical Research Council | URL: www.australianclinicaltrials.gov.au/researchers/research-principles-and-guidelines (accessed 20 April 2018) | Generic:The number of subjects planned to be enrolled. In multicentre trials, the numbers of enrolled subjects projected for each trial site should be specified. Reason for choice of sample size, including reflections on (or calculations of) the power of the trial and clinical justification© Commonwealth of Australia 2014. This work is licensed under a Creative Commons Attribution 3.0 Australia License2019© Commonwealth of Australia 2014.https://creativecommons.org/licenses/by/3.0/au/ |
| Agency for Healthcare Research & Quality | URL: www.ahrq.gov/ (accessed 20 April 2018) | No specific relevant guidance |
Appendix 3 Conventional approach to a randomised controlled trial sample size calculation
Sample size calculations for a randomised controlled trial
Statistical sample size calculation is not an exact, or pure, science. 32,172 First, investigators typically make assumptions that are a simplification of the anticipated analysis. For example, the impact of controlling for prognostic factors is very difficult to quantify and, even though the analysis is intended to be adjusted (e.g. when randomisation has been stratified or minimised),173 the sample size calculation is often based on an unadjusted analysis. Second, the calculated sample size can be very sensitive to the values of the inputs. In some circumstances a relatively small change in the value of one of the inputs (e.g. the control group event proportion for a binary outcome) can lead to a substantial change in the calculated sample size. However, the value used for one of the inputs (e.g. control group event proportion) may not accurately reflect the actual value that will be observed in the study. It is prudent to undertake sensitivity calculations to assess the potential impact of misspecification of key inputs (e.g. SD for a continuous outcome, level of missing data, etc.). This would also help inform decision-making about the continuation of a trial in which accumulating data suggest that the parameter will be substantially different from the one assumed in the main sample size calculation.
The role of the sample size calculation is to determine how many observations are required in order that the planned main analysis of the primary outcome, that is the one chosen to address the primary estimand of interest, is likely to provide a useful result. The sample size may also be chosen with reference to further key analyses (e.g. those focusing on other outcomes and subpopulations that address alternative estimands of interest). Most simply, this can be done by choosing the RCT’s sample size to maximise the number of participants required across the various analyses under consideration.
A variety of statistical approaches are available, although, overwhelmingly, current practice is to use the conventional Neyman–Pearson approach. This is so much the case that the specification of ‘effect size’, ‘significance level’ and ‘power’ are common parlance. The Neyman–Pearson approach is explained in Appendix 2 and the rest of this appendix assumes this approach is being used. Alternative approaches to the sample size calculation are briefly considered in Appendix 4 (see Appendix 4, sections Precision; Bayesian; and Value of information approach).
Often a simple formula can be used to calculate the required sample size. 174 The formula varies according to the type of outcome and, somewhat implicitly, the design of the trial and the planned analysis. Some of the simpler formulae are given in Binary outcome sample size calculation for a superiority trial; Continuous outcome sample size calculation for a superiority trial; Dealing with missing data for binary and continuous outcomes; and Time-to-event sample size calculation for a superiority trial, for the standard RCT design (i.e. a two-arm parallel-group RCT) and for the most common outcome types (binary, continuous and time to event).
Neyman–Pearson approach
The most common approach to the sample size calculation for a RCT is based on what can be described as the Neyman–Pearson, or conventional, approach. In essence, this approach involves adopting a statistical hypothesis testing framework and calculating the sample size required, given the specification of two statistical parameters (the power and significance level – see Glossary for definitions). This approach is sometimes referred to as carrying out a ‘power calculation’. This is a frequentist (as opposed to Bayesian) approach to answering the research question (see Appendix 4).
Although it is often not explicitly stated, this approach involves assuming a null hypothesis for which evidence to reject in favour of an alternative hypothesis is assessed. For a superiority trial with a standard design, the null hypothesis is that there is no difference between the interventions, and the alternative hypothesis is that there is a difference between them (i.e. one is superior to the other with respect to the outcome of interest). This leads to four possible scenarios once the trial is conducted and the data have been collected and analysed (Table 7).
| Truth | Statistical analysis result | |
|---|---|---|
| Statistically significant | Not-statistically significant | |
| There is a genuine difference between the interventions | Correctly concluding there is a difference (true positive)a | Wrongly concluding there is a not a difference when there is; type II error (false negative)b |
| There is not a genuine difference between the interventions | Wrongly concluding there is a difference when there is not; type I error (false positive)c | Correctly concluding there is no difference (true negative) |
There are two scenarios in which a correct conclusion is made and two scenarios in which an incorrect conclusion is made. The chance of these two errors is controlled by the statistical parameters, the significance level and the statistical power. Typically, the probability of the type I error (α) is controlled to be 0.05 (or 5%), which is achieved by using this level as the one with which it is concluded that the result is statistically significant (i.e. a probability of ≤ 0.05 is ‘statistically significant’ and > 0.05 is not). Additionally, this is usually a two-sided significance level, in that it is not prescribed a priori in which direction a difference might be found. In a similar manner, we can also control the type II error rate (β) by ensuring that the statistical power (which is simply 1 minus the type II error rate, i.e. 1 – β) is sufficiently large. Typical values are 0.8 or 0.9 (i.e. 80% or 90% statistical power).
It is worth noting that the presence or absence of a statistically significant result cannot be used to decide whether or not there is an important difference. Often the most that can be concluded from a non-statistically significant result is that there is no statistical evidence of a difference (i.e. a difference cannot be conclusively ruled out). Additionally, it is possible to have a statistically significant result even when the observed difference is smaller than the target difference assumed in a conventional sample size calculation. 175,176 This value can be readily calculated for a continuous outcome. Here, this is described as the minimum statistically detectable difference. It should not be confused with the MCDC or the minimum clinically detectable difference, which are entirely different concepts (see the Glossary for brief descriptions). Some recommend calculating and reporting the minimum statistically detectable difference, as well as the target difference and the required sample size. 176
Both the use of the 5% significance level and 80% or 90% power are arbitrary and have no theoretical justification, but are widely used. However, as excluding the possibility of either error is impossible, and the required sample size increases at a greater rate the closer either error rate is set to zero, these values have become the de facto standards. If well chosen, the target difference is a valuable aid to the interpretation of the analysis result, irrespective of whether or not it is statistically significant. It is essential when interpreting the analysis of a trial to consider the uncertainty in the estimate, which is reflected in the CI. A key question of interest is what magnitude of difference can be ruled out. The expected (predicted) width of the CI can be determined for a given target difference and sample size calculation, which is a helpful further aid in making an informed choice about this part of a trial’s design. 98
Given the assumed research hypothesis, the design, the statistical parameters and the target difference, the sample size can be calculated. Formulae vary according to the type of outcome (see Binary outcome sample size calculation for a superiority trial; Continuous outcome sample size calculation for a superiority trial; and Time-to-event sample size calculation for a superiority trial), study design (see Appendix 5 for some common alternative designs) and the planned statistical analysis (see Other topics of interest). The general approach is similar across study designs. In more complex situations, the frequentist properties (e.g. the type I and II error rates) can be estimated using simulations of data and consequential analysis of simulated results for scenarios in which there is and is not a genuine difference between interventions. 177
The conventional approach to sample size calculations is not without limitations. 168,178,179 Misinterpretation of findings, related at least in part to the statistical approach (such as what a p-value actually is and what can be inferred from it), has been highlighted and various proposal to improve practice have been made. 180 Nevertheless, the conventional approach to clinical trial sample sizes has remained remarkably persistent and is by far the most common currently used. 13,181 This reflects to some degree its ease of implementation and training, as well as the uncertainty about alternatives.
This appendix presumes the conventional approach is to be used for the sample size calculation for a two-arm trial with 1 : 1 allocation. Immediately below, simple formulae for the most common outcome types are provided. For completeness, Appendix 4 briefly summarises alternative approaches to calculating the sample size for a RCT. Statistical issues related to conducting a reassessment of the sample size under a conventional and a Bayesian approach are considered elsewhere. 1,182–184 Adaptive trial design (see Appendix 5) seek to formally incorporate potential changes to the design due to interim data into the trial design.
Binary outcome sample size calculation for a superiority trial
There are a number of commonly used formulae for calculating the sample size for a binary outcome for a superiority trial (i.e. for a study in which two proportions are to be compared). 1 One formula for the required number of participants per arm, n, for a standard trial (assumed equal allocation and therefore group sizes) is presented in Equation 1 and is relatively straightforward to calculate:
where n is the required number of observations in each of the two randomised groups. Z1 – x is the value from the standardised normal distribution for which the probability of exceeding it is x. πA and πB are the anticipated probability of an event in groups A and B. α is the statistical significance level (i.e. the type I error rate), and β is the type II error rate and is chosen so that 1 – β is equal to the desired statistical power. The formula assumes even allocation between the treatment arms and a two-sided comparison.
The target difference can be expressed in multiple ways. It can be expressed as the absolute risk difference (πB – πA) or as a ratio, typically the RR: (2)(πB/πA) or OR: (3)(πB/(1−πB)πA/(1−πA)).
Different combinations of πA and πB can lead to the same OR or RR, although they may produce very different absolute risk differences. For example, a proportion of 0.4 compared with one of 0.2 represents a RR of 2 and a risk difference of 0.2. Proportions of 0.1 and 0.05 also represent a RR of 2, but the risk difference of 0.05 is far smaller and will require a far larger sample size. Whenever the target difference is expressed as a ratio, the anticipated control (reference) group risk, πA, should also be provided.
The value assumed for πA greatly influences the sample size. 1 In this context the control group proportion can be considered as a nuisance parameter with the target difference, δ, fixed regardless of what the control group proportion is. Estimates of this parameter may come from a pilot trial or existing literature (see Chapter 3, Pilot studies and Review of the evidence base). There needs to be an evaluation of the observed response dependent on the study design, population and analysis in the study from which it is being estimated. The planned analysis, particularly the summary measure used, is important for the calculation as adjusted and unadjusted analyses can be estimating different estimands. 185
Continuous outcome sample size calculation for a superiority trial
For ease of presentation, a slightly simplified formula124 to estimate the sample size per arm for a superiority trial with a continuous outcome is:
where Z1 – β and Z1 – α/2 are defined as before, σ is the population SD and δ is the target mean difference. As before, the formula presented here assumes even allocation between the treatment arms and a two-sided test comparison.
In practice, σ is typically assumed to be known, with an estimate from an existing study, S, used as if it were the population value. The formula can be further simplified by replacing δ by δσ, the Cohen’s d standardised effect (dSES):
Specifying the effect on the standardised scale, dSES, is therefore sufficient to calculate the required n for a given significance level and power. However, it should be noted that different combinations of mean and SD values produce the same SES (Cohen’s d). See Chapter 3, Standardised effect size, for further discussion. Although sufficient for the sample size calculation, specifying the target difference as a standardised effect alone can be viewed as an insufficient specification as it does not define the target difference in the original scale.
A key component in the sample size calculation of a continuous measure is the assumed magnitude of variance. An estimate of this parameter (usually expressed as a SD) may come from a pilot trial or existing literature (see Chapter 3, Pilot studies and Review of the evidence base). It is possible to get into a ‘Gordian knot’ when looking for an estimate of the variance. Ideally, an estimate of the variance taken from a large clinical study in the intended trial population with the same interventions would be available. However, if such a study was available, a new trial would probably not be necessary. If a new trial is truly needed, that need implies some limitations in the existing evidence. To decide on the relative utility of the variance estimates, various aspects of the study need to be considered (e.g. study design, population, outcome, analysis conducted, etc.), in a similar manner to the control group proportion and any estimate of a realistic target difference (see Chapter 3, General considerations, Pilot studies and Review of the evidence base). 1,124 The accuracy of the variance estimate will obviously influence the sensitivity of the trial to the assumptions made about the variance and will also influence the strategy of an individual clinical trial.
A more accurate, although computationally more demanding calculation if performed by hand, will give a slightly different result from the formula above (see Equation 5) and is used in various sample size software. 186 The difference between the simple and more complicated formulae is that the simple calculation assumes that the population variance, σ, is known for the design and analysis of the trial. The more complicated calculation recognises that, in practice, the sample variance estimate, s, will be used when analysing the trial. The more accurate formula can be found elsewhere. 1
Dealing with missing data for binary and continuous outcomes
In most studies involving humans, it is likely that withdrawals, losses to follow-up and missing data will occur during the trial. 187 Individuals in a trial could decide that they no longer want to take part and completely withdraw from the trial, they could move during the study and not update the study team, and/or they could decide that they do not want to answer a particular question on a questionnaire. Even in the most well-designed and well-executed trial, some losses to follow-up are inevitable. Additionally, intercurrent events (e.g. death or change in treatment) may preclude the possibility of an outcome under the conditions implied by the trial’s aim and corresponding estimand of interest.
Irrespective of the reasons for missing data, sample sizes are frequently inflated to account for a degree of missing data during the study. The estimate of the extent of missing data is often gathered from a pilot trial, previous studies of the intervention, or trials in a similar population. In the presence of missing data, the power of a trial to detect the same target difference is reduced, hence the need for inflation of the sample size. To inflate the sample size to account for missing data, the overall sample size required, 2n, is divided by the proportion of data anticipated to be available for analysis (p0b):
For example, if 20% attrition is anticipated, then the target sample size is divided by 0.8. A more complex and accurate approach can be used to deal with loss to follow-up over time, which is particularly pertinent for time-to-event outcomes.
It should be noted that adjustments such as above deal with the impact only in terms of precision of the missing data; a substantial number of missing data may also put the study results at risk of bias (e.g. if the reasons for attrition are related to eventual outcomes).
Time-to-event sample size calculation for a superiority trial
Owing to varying time of follow-up across study participants, it is not appropriate to analyse the proportion of participants who experience an event using logistic regression or a similar method. The analysis, and therefore the calculation of the sample size, for time-to-event data is also complicated by the fact that not all individuals will experience the event of interest. As a consequence, it is not appropriate to simply compare mean observation times directly between groups. There are three main approaches to the sample size calculation for this type of outcome:
-
compare Kaplan–Meier survival curves, using the logrank test or one of several other similar methods
-
assume a particular model form without specifying the survival distribution [e.g. the Cox (proportional hazards) regression approach]
-
use a mathematical model for the survival times and hence for the survival curve, such as the exponential or the Weibull distributions.
For ease of discussion, the term ‘survival’ is used to refer to the non-occurrence of the event by a specific time point and does not imply restriction of the methods to looking at mortality. The first two sample size methods are much more common than the third. For either a logrank- or Cox regression-based analysis, the analysis does not imply a specific distribution for the survival curve. The proportion surviving at any time point during the follow-up can be estimated to avoid having to assume one for the purpose of the sample size calculation. A target difference is inferred, explicitly or implicitly, for all of the methods. It is commonly expressed as a HR. 188 Similarly, to a binary outcome, adjusted and unadjusted analyses can estimate different estimands. 189
The difference between the two groups can be expressed as a difference between the survival probabilities at a specified time point. The data can be analysed accordingly, using the Greenwood standard errors to compare survival proportions. 190 However, this is statistically not a good way to compare groups, as it depends on the chosen time point and does not use the data on survival beyond that point. A method that takes all of the observed survival times into account, such as the log-rank test, is more convenient and statistically efficient. This is a test of statistical significance that has no explicit associated estimate of the treatment effect. Despite this, a power calculation can be performed by characterising the two survival curves by their median survival time, the time when half of the population in the group is estimated to have experienced an event.
To infer information about the survival curve from the median survival time, it must be assumed that the survival curve follows a known mathematical pattern, even though this assumption may not be used in the analysis. For example, the survival curve can be (and commonly is) assumed to be an exponential decay curve. The survival proportion (πA) for treatment A at some time t can then be used to estimate the median survival time m, as follows:
Instead of a difference between mean times and the SD of times that would have occurred if we were comparing the average survival time in which all participants had reached the event, there are two median survival times or, equivalently, the median survival time in one group and the difference between medians, which can be considered the target difference. This is an implicit treatment effect size, although no such estimate is produced by the log-rank test.
Alternatively, an assumption about the difference between the survival curves, the proportional hazards assumption, can be made. This is the assumption that the ratio of the risk of an event in one group over a given short time interval, to the risk of an event in the other group over the same time interval, is constant over the follow-up period. This ratio is the HR and is the parameter that we estimate in Cox proportional hazards regression. This HR can be considered to represent the target difference (albeit on a relative range). However, another parameter is still needed to characterise the survival curve, such as the median survival time in one group.
It is possible to characterise the target difference either as the difference between median survival times or the HR, or by comparing events as an absolute difference in the event rate at a specific time point. Whichever approach is taken, the median survival in the control group or some similar parameter is needed to fully and uniquely specify the target difference. The statistical power of the comparison will depend on the total number of events rather than the total number of participants. A large number of events will imply high power. Participants who do not experience an event contribute little to the power. The median survival time and the planned follow-up time enable the number of events that will occur to be estimated.
Things become more complex if participants are recruited over a time period and then all followed up to the same calendar date. This results in widely varying follow-up times for censored cases. To allow for this, the recruitment period needs to be accounted for in the sample size calculation. If each participant will be followed for the same length of time, such as 1 year, the calculation is as if all were recruited simultaneously.
Methods for estimating the sample size usually rely on the number of events that need to be observed. The additional assumption of an exponential survival curve is typically made. Under these circumstances, the hazard, the instantaneous risk of an event, is a constant over time. The proportional hazards assumption is thus automatically satisfied. The HR can then be calculated as:
Again, under the assumption of an exponential survival distribution for both interventions, we can estimate the required number of events, eA, in one group by:
This can be doubled for the other group, or the HR can be used to calculate the number of events in the other group. Having calculated the number of events needed, the number of participants required to produce this number of events can be calculated. To do so requires making further assumptions regarding the survival distributions for each group, the length of follow-up and any censoring of data. A varying length of follow-up according to the accrual pattern is also typically assumed to make maximum value of those recruited early in the recruitment period and avoid unnecessarily extending the follow-up of the final participants. This issue is beyond the scope of this document, but further discussion can be found here. 1 Sample size calculations which allow for non-proportional hazards are also possible. 191
The target difference for this type of outcome can be variously expressed as a difference between the median survival times (mB – mA), the difference between the proportions surviving at a particular point in time (πB – πA), or the HR (which might vary over time). It is worth noting that, as for the other outcome types, how intercurrent events (e.g. change in treatment) are dealt with needs careful consideration and, similarly, the reasons for censoring needs assessing, as not all may be viewed equally. For example, if death is not the event of interest, then the occurrence of a death leads to censoring of the outcome of interest. However, it may be viewed as indicative of the likelihood of such an event occurring or as precluding the event from occurring with no impact on the likelihood (e.g. the death of someone who has had a knee joint replacement precludes the failure of the device due to wear and tear). The handling of such occurrences in the analysis and the corresponding impact on the sample size (and, in this context, the anticipated target difference and event rate) should be considered with reference to the estimand of interest.
Other topics of interest
Adjusting the sample size calculation of a continuous outcome for a baseline measurement
For a continuous outcome measure, full specification of the target difference requires both the mean difference and the corresponding SD to be stated. If a baseline measure of the same continuous measure is also collected, then it is possible to adjust the comparison of means for the baseline value (at the individual participant level) and thereby to incorporate the correlation between the baseline and follow-up measure into the sample size calculation. A simple formula has been proposed to account for this correlation and is sometimes called a design effect or variance (deflation) factor. 140 The sample size, accounting for the correlation between the baseline and follow-up values, for a comparison of two means for a specified target difference is:
where n is as before (the number needed per group from a calculation without adjustment for baseline) and q is the correlation between the baseline and subsequent outcome measure.
For example, consider a parallel two-arm superiority trial with a primary outcome measure of the Short Form questionnaire-36 items mental component score at 6 months, which is also taken at baseline. A target sample size of 266 subjects is calculated, assuming 90% power, 5% alpha, an 8-point difference and a SD of 20. Previous studies have shown that the correlation between repeated measures of the Short Form questionnaire-36 items can be as high as 0.8 and as low as 0.6, which would lead to quite different numbers of required participants. If a more conservative choice is made, and a correlation of 0.6 is assumed, the required sample size is then:
If baseline/change score corrections are made, then it is vital to make a credible assumption regarding the correlation. Similar to specifying the target difference, the anticipated correlation value may be estimated from previous trials or observational data. The key advantage of incorporating the correlation between these two measures into the sample size calculation is that fewer subjects are required for the RCT. The key disadvantages are that another assumption is being made and, if the observed correlation is much lower than anticipated, then the trial will be underpowered to detect the target difference specified.
Compliance-adjusted sample size
An ITT-based analysis is the widely accepted default analysis for RCTs. It estimates the average treatment effect in the full randomised cohort, irrespective of compliance with the treatment allocation. 24 Such a focus can alternatively be expressed as the desire to assess the ‘effectiveness’ of the treatment as opposed to the ‘efficacy’. 22,23 More specifically, it may be said to imply a treatment policy-based estimand.
The impact of compliance on the anticipated average treatment effect can be taken into account by down-weighting the anticipated causal effect to allow for departures from randomised treatment (also referred to as non-compliance or non-adherence). 192,193 A natural additional aspect of interest is the treatment effect among those who ‘comply’ (receive the treatment as allocated); this is often described as the complier-average causal effect (CACE). This can be viewed as leading to an ‘efficacy’ focus analysis192 and, more specifically, a principal stratum-based estimand. 23,194
The most simplistic compliance scenario is a standard trial design with all or nothing compliance (i.e. each participant either does or does not comply), for which the impact of compliance can be relatively straightforwardly accounted for. For this setting, the relationship between the target difference for a full trial population (irrespective of compliance) and among compliers only can be readily expressed.
For a binary outcome, a corresponding approach for a RR is:
where pcA and pcB are the proportion of non-compliance among the randomised intervention groups A and B, and RRCACE and RRITT are the RR ratio among compliers and the ITT population, respectively.
For a continuous outcome, the impact of non-compliance in the intervention arm can be taken into account by multiplying the treatment effect between the groups for compliers (δCACE) by the level of non-compliance in the intervention (pc), to get an overall (δITT) treatment effect:
An alternative formula is needed if non-compliance can occur in both arms. 193,195 Trial sample size calculations are typically for an analysis that will estimate an ITT-based effect (or a treatment policy estimand). Compliance is not often explicitly considered in RCT sample size calculations. From one perspective, if the chosen target difference is one that is considered to be important to stakeholders for the population of interest, then compliance does not need to be part of the formal calculation. Instead, the presence of non-compliance is merely one of a number of reasons that may explain why this target difference might not be observed or that may lead to missing data. Alternatively, if the treatment effect in a compliant population can be specified (e.g. from a previous study), compliance could be taken into account, as shown in Compliance-adjusted sample size, to show that an effect that is realistic in an ITT population (or treatment policy estimand) is still detectable (and still of a magnitude that would be considered important).
It is worth noting that harms are typically analysed according to the treatment-received groups and, therefore, the above calculations are not appropriate. More complex analysis approaches for exploring compliance are possible. Compliance analyses often suffer from lack of precision (particularly CACE analyses) and this is an active area of research. 192,196
Appendix 4 Alternative approaches to the sample size calculation for a randomised controlled trial
Introduction
Three main alternative approaches (precision, Bayesian and value of information) to sample size calculations are briefly considered in turn below. Other approaches exist, although at present they are rarely used. 179,197
Precision
The limitations of the conventional approach to the sample size calculation of a RCT are well known. 32,178 One alternative is to base the sample size on the precision of the estimate of the interest, the treatment difference. This can be expressed through the CI, and the sample size can be chosen to achieve a CI of a particular interval width (i.e. difference between the upper and lower limits). The width of the 95% CI for a standard trial design for a binary outcome is related to sample size via the relation:
where p is the expected mean response across treatment groups, w is the width of the CI for the difference in proportions, which could be chosen to exclude the magnitude of difference desired to be detected and n is the number in each group. This formula makes use of the large sample binomial approximation. More complex calculations for the CI can be used instead, although with limited additional value for many situations.
-
The width of the 95% CI for a standard trial design for a continuous measure is related to sample size via the relation:
where w is the width of the CI for the mean difference, which could be chosen to exclude an important difference, S is the population SD (assumed to be known) and n is the number in each group.
For both of the above formulae (see Equations 14 and 15), two-sided CIs with confidence level (1 – α) can be calculated by substituting the corresponding Z1 – α/2 in place of 1.96. For example, a 90% CI would use 1.645 instead of 1.96. These calculations implicitly do not take into account statistical power and will lead to a smaller sample size, given equivalent assumptions. This type of approach is increasingly used in the context of pilot trials (e.g. for ensuring that the width of the CI for the group proportion or consent rate is sufficiently narrow). 165,198–200 However, use in the context of a definitive trial is limited to date. 13,178,201 The issue of the magnitude of a difference that is valuable to be observed is still present.
Bayesian
The Bayesian concept of assurance,12 also referred to as ‘average power’202 or a ‘hybrid’ Bayesian–frequentist method,11,203 can be used to inform the sample size calculation for a trial that is to be analysed within a conventional (Neyman–Pearson) framework. In this context, assurance is the unconditional probability that a trial will yield a statistically significant result, calculated by averaging the statistical power across a joint prior distribution for the treatment difference and any unknown relevant nuisance parameters (such as the response variance or control response rate for continuous or binary outcomes, respectively). High assurance implies that the trial is adequately powered to detect a continuum of plausible effects. This increases the robustness of the design but typically leads to larger than conventional sample sizes. 203
When performing assurance calculations, a prior distribution for the treatment difference can be determined from expert opinion (see Chapter 3, Opinion-seeking) or a synthesis of existing data (see Chapter 3, Pilot studies and Review of the evidence base). Adjustment for between-trial heterogeneity204,205 and the bias inherent in existing effect estimates can be made. 206 The latter arises because Phase II trials may be more at risk of internal biases and confirmatory trials are commissioned only after observing promising early phase results. A careful choice of prior distribution (possibly truncated to support only alternative values of the treatment effect) is needed to ensure that sample sizes are not unreasonably large and that assurance approaches one as the sample size becomes infinitely large. 203 A related approach avoiding this last subtlety is ‘conditional expected power’, defined as the average power calculated, assuming that an advantage for the novel intervention must exist. 207 In this setting, one can set the target difference (δ) to the value δ*, which ensures that a conventional RCT designed to high frequentist power to detect δ* also has high conditional expected power. 208
A wide variety of methods for calculating the sample size of a Bayesian RCT also exist. The average power of trials with Bayesian final decision rules can be calculated. 209 Alternatively, the sample size of a Bayesian trial can be chosen to ensure that there is a high prior predictive probability of the trial concluding with definitive levels of evidence, supporting either adoption or abandonment of the novel intervention, thus reducing the region of indecision. 210 Alternatively, precision-based approaches calibrate a trial’s sample size on the basis of the expected length of a 100(1 – α)% posterior credible interval or the expected coverage of an interval of fixed width. 211 Judgements about what constitutes an acceptable length or coverage level will depend on how the trial results will feed into subsequent decision-making.
Value of information approach
Bayesian decision-theoretic designs exist that choose the sample size to maximise the expected utility of the trial. 212,213 This is implemented in health technology assessments as a value of information analysis. An efficient sample size is determined by comparing the (expected) cost of conducting a study of sample size, n, with the expected value of the information that the study will yield. 168,214 As such, it offers a radically different approach to determining the sample size for a RCT from the conventional (Neyman–Pearson) power calculation approach. A key element of the decision-theoretic approach is the focus on expected values rather than hypothesis testing for making decisions. 214
The cost of collecting information is simply the budget for a proposed clinical trial of sample size n. The information the trial yields is valued in terms of its ability to reduce uncertainty; all else being equal, larger trials will yield more information than smaller ones. The value of the information is the ‘expected reduction in the expected loss’ from that study.
The logic is as follows: a decision must be made whether to adopt or reject a new treatment. As the decision is made under conditions of uncertainty, the ‘wrong’ decision could be made. The expected loss associated with the decision is the probability of making the wrong decision, multiplied by the loss (forgone health gain) if the wrong decision is made. More research (i.e. information in the form of a clinical trial or other data-gathering exercise) reduces the probability of error and hence reduces the expected loss. This expected reduction in expected loss is the expected value of sample information. Expected value of sample information can be measured in terms of health gain (e.g. life-years or quality-adjusted life-years) forgone, or it can be expressed in monetary terms. For example, the National Institute for Health and Care Excellence in England values a quality-adjusted life-year at between £20,000 and £30,000. 68 The expected net gain of sampling is the difference between the expected value of sample information and the anticipated cost of the study. The most efficient sample size for the study is that which maximises the expected net gain of sampling. Use of a value of information approach is an active area of research and various modifications to the basic approach have been proposed. 155,168,215
Appendix 5 Specifying the target difference for alternative trial designs
Introduction
Five types of alternative trial (multiarm, cluster, crossover, biomarker and adaptive) designs are considered in turn below, in terms of their implications for specifying the target difference. A huge number of variations in trial designs (e.g. split-plot216 and stepped wedge designs217) exist although, in terms of the implications for specifying the target difference, the relevant issues are typically similar to those addressed below.
Multiarm
There are many different designs and aims of multiarm trials, but the one thing that they have in common is that they all include more than two trial arms. For example, this could involve comparing multiple treatments against a common active control or comparing two or more treatments against a placebo. Specifying the target difference in multiarm trials is more complicated than a parallel two-arm trial, as multiarm trials aim to answer multiple research questions. The sample size has to be sufficient to address each research question and therefore multiple target differences could be appropriate.
The more trial arms there are, the more complicated the process becomes. In a trial with three intervention arms comparing treatments A, B and C, there are seven theoretically possible comparisons that could be made: A versus B; B versus C; A versus C; AB versus C; AC versus B; BC versus A; and A versus B versus C (using a global test). An example is given in Box 12. A key aspect of the design of multiarm trials is specifying what the estimand of interest is, which comparisons are of most interest and which hypotheses will be tested. The selection of comparisons may become simpler if one of the arms (say C) is a control arm, such as usual care or placebo. In this instance, what would be of primary interest would be treatment A compared with the control C, and treatment B compared with C. The simplistic approach to sample size calculation would be to consider each of these pairwise comparisons as if they were separate trials. The target difference for each would require specification and justification in the same manner as a standard trial, even though these might well be the same for both. It might also be of interest to compare A with B directly, although specifying that difference might depend on whether treatments A and B are different types of interventions, minor variations of the same intervention (e.g. doses of the same drug), or an experimental treatment and an active comparator, etc.
We calculated the sample size for this three-arm trial on the basis of the comparison treatment (cervical collar or physiotherapy) vs. a wait and see policy, with equal allocation to the treatment arms and three repeated measurements (at entry and at 3 and 6 weeks’ follow-up), with an estimated correlation coefficient of the measurements of p = 0.7 and a difference in the mean value of the visual analogue scale for arm pain of 10 mm, as a clinical relevant difference with an estimated SD in each treatment group of 30 mm. As arm pain is the main complaint in cervical radiculopathy, we chose this outcome for calculating the sample size. The total sample size needed to detect this difference at a 5% level of significance with a power of 90% was 240 patients (80 patients per group).
This is an open-access article distributed under the terms of the Creative Commons Attribution Non-commercial License, which permits use, distribution, and reproduction in any medium, provided the original work is properly cited, the use is non commercial and is otherwise in compliance with the license. See: http://creativecommons.org/licenses/by-nc/2.0/ and http://creativecommons.org/licenses/by-nc/2.0/legalcode.
Multiple arms allow more than one hypothesis to be explored; however, if it is appropriate to specify the most important hypothesis under study this can then be used to drive the sample size. In the example described above, it could be that treatment arm A compared with the placebo is of most importance and the comparisons of the treatment arms can thus be done in a hierarchy. 219 This would have consequent effects on specifying the target difference, as it would be the same as a parallel two-arm trial as previously outlined, with the comparison of A with the placebo primarily determining the sample size. If the aim is to look at the specified comparisons simultaneously, then there will be multiple target differences that could be used, depending on the comparison being made. In the example above, this would mean that both treatment arm A and treatment arm B must be statistically different from the placebo for the study to be declared a success. Such studies are termed multiple must-win trials. 220
When there are multiple target differences, the smallest target difference will be the one that has the biggest influence on the sample size calculation. 220 When appropriate, the use of global comparison tests, pairwise comparisons and/or statistical multiplicity adjustments can be used to account for multiple comparisons. 221
Cluster randomised
Cluster RCTs involve randomising groups or clusters of individuals to trial arms rather than the individuals themselves. If cluster randomisation is used, then this needs to be accounted for within the design and analysis of the study, including the sample size calculation. 222 Individuals within each cluster will be more alike than they are like individuals within other clusters and cannot be considered independent of each other. The ICC is a measure of this similarity and for a particular outcome represents the amount of variance that can be explained by the variation between clusters. Sample size calculations for cluster trials have been developed and involve inflating the sample size for an equivalent individually randomised trial by a design effect (also called a variance inflation factor):223
where m is the average cluster size and p is the ICC. This formula can be used for binary and continuous outcomes.
For example, in an individually randomised trial of an exercise intervention for low back pain, the target difference was 1.57 points with a SD of 4. Assuming 90% statistical power and 5% two-sided significance level, a target sample size would be 274. If this trial were undertaken as a cluster RCT, then the target sample size, assuming an average cluster size of 20 and ICC = 0.03, would be:
With a sample size of 432 and 20 individuals per cluster, this would require 22 clusters to be randomised (i.e. 440 individuals in total). This increases the sample size substantially compared with individual randomisation, for which a target sample size of 274 would be required.
The ICC, as a ratio, is a difficult quantity to estimate precisely. 224 Pilot trials and most clinical studies are too small to achieve this. Instead, databases of estimates from other data sources, which include similar RCTs, exist, so that the same or at least a similar outcome can be used to provide or inform the choice of a more reliable value. Existing databases of ICC values cover implementation science, organisational interventions and surgical interventions. 121,224,225
The calculations above for the design effect do not take into account variation in cluster sizes and assume that the same, or approximately the same, number of individuals per cluster are recruited. 226 If there is variation in cluster sizes, then the formula above will underestimate the adjustment required. An additional factor that needs to be considered in trials that anticipate variation in cluster sizes is the coefficient of variation (CV). The CV is the ratio of the SD of cluster sizes to the mean cluster size. The design effect is expressed as:
where m is the average cluster size and p is the ICC.
The maximum increase in sample size when accounting for variation in cluster size is CV2 + 1. The choice of CV is important to ensure that the appropriate inflation factor is estimated. A number of different methods for different scenarios have been proposed to estimate this coefficient:227 knowledge of CVs observed in previous studies; investigating and modelling sources of cluster size variation; estimating likely minimum and maximum cluster sizes; when all individuals in each recruited cluster participate in a trial; when cluster sizes are identical; and when cluster size follows a roughly normal distribution. It has been recommended that the potential impact of variation in cluster sizes should be explored when planning sample size calculations for cluster trials. In particular, it becomes important to assess this when large variations in cluster size, large ICC values or large mean cluster sizes are anticipated.
It is not always necessary to incorporate the CV into the cluster trial sample size. If the CV is estimated to be < 0.23, then the sample size does not need to be adjusted for the variation in cluster size as the impact on the sample size is negligible. 226
Clustering can also potentially arise in individually randomised trials, when interventions are delivered within a group setting or when individual therapists deliver the intervention on an individual basis to a group of individuals. 228 The same methods outlined above apply in these situations but, depending on the type of interventions and nature of the clustering, this may be required in only one of the trial arms.
Crossover trial
Crossover (randomised) trials involve randomising individuals to a sequence of interventions rather than to a single intervention. 229 In the simplest form, they involve two treatments and two periods (a 2 × 2 crossover trial, also known as an AB/BA trial). More complex designs, with three or more interventions and/or periods, are possible. 1,229 Here, consideration is restricted to the 2 × 2 crossover design and specifically the most common implementation in which AB and BA sequences are used equally. For a binary outcome, the sample size can be calculated in terms of the conditional OR (anticipating an analysis using McNemar’s test) and approximated as:
where pA and pB are the probability of an event under treatment A and B, respectively. The number of participants (with outcomes for both treatments) is:
with Z1 – α/2 and Z1 – β defined as before.
It should be noted that the standardised effects (here expressed as ORs) for a parallel-group and crossover trial are not equivalent. In terms of expressing the target difference, the absolute difference along with the control group proportion is the most transparent [i.e. (πB – πA) and πA].
For a continuous outcome, a similar formula to the parallel-group superiority trial can be used:
with δ, Z1 – α/2 and Z1 – β defined as before. However, unlike before, here σ refers to the anticipated within-person variance and not the pooled variance of two independent treatment groups. Here, n refers to the overall sample size, as well as the number receiving each treatment. The crossover design enables the individual variance to be stripped out, leading to a more precise estimate and smaller sample size. In terms of target difference on the absolute level, it remains as before. As for the binary outcome situation above (see Equation 19), it is noteworthy that expressing the target difference as a SES, when calculated simply by using the inputs to the sample size calculation for a crossover, is not directly comparable with a parallel-group trial, even though the absolute target difference is the same. They will be equivalent only in the improbable event that the within-person correlation is zero. For example, given a target absolute difference of 10 points, anticipated intervention group SD of 30 and within-subject variance of 19, we would obtain markedly different SESs of 0.33 and 0.63, respectively. The pooled individual group SD is preferred when expressing an effect size as a standardised mean difference, even where a crossover trial is planned.
It should be noted that the impact of missing data on precision is more marked for a crossover trial than for a similarly sized parallel-group trial.
Biomarkers
The sample size considerations required for biomarker-stratified trials do not differ substantially from those required for non-stratified trials, but there are some additional considerations that are important. The common components of a sample size calculation still apply [e.g. for a binary outcome, the significance level, statistical power, event proportion in the control arm and the target difference being sought (δ)]. However, these components tend to be considered separately within each of the proposed biomarker stratum. Other considerations are briefly covered below.
Type and prevalence of the biomarker
There are various types of biomarkers, but, in the main, they can be classified into two predominant types: (1) prognostic and (2) treatment selection biomarkers. Prognostic biomarkers stratify patients on the basis of the prognosis of the disease in the absence of treatment and, thus, they relate to the natural history of the disease. Treatment selection biomarkers (also known as predictive biomarkers) stratify patients on the basis of their expected response (or not) to a particular treatment. Some biomarkers demonstrate both prognostic and predictive qualities. When designing a biomarker-stratified trial and performing sample size calculations, it is important to be aware of any existing data that describe the discriminatory performance of the biomarker in question, whether it be prognostic, predictive or both. In particular, if a biomarker is prognostic, then the event proportion in the control arm will differ between strata, which may influence the sample size needed for each group.
The prevalence of the biomarker in question will affect the availability of patients for a particular biomarker stratum and, if rare, this could limit not only the recruitment rate, but also the power with which an intervention can be tested in that group. Trials that use an enrichment strategy (in which the new intervention is tested in only the biomarker-positive group first) can be an efficient way of testing for benefit. This approach can be used in trials testing targeted drug therapies that have been designed to act on a specific molecular pathway, such that if insufficient benefit is seen in the biomarker group with that molecular aberration, there is very little likelihood of a benefit being seen in the group with a normal molecular pathway. However, the trial can be expanded to test biomarker specificity by including the biomarker-negative group later, if adequate activity is seen in the biomarker-positive group.
Testing for interaction
In some cases, it may be advisable to power the trial on the basis of detecting a statistically significant interaction between biomarker strata. In this case, the target difference is the difference in treatment effects, rather than the overall treatment difference in outcome, between randomised groups. However, attaining adequate statistical power for a test of interaction can lead to a potentially unfeasible sample size.
Although the presence of a statistically significant interaction may be compelling, it does not follow that a stratified medicine approach will be the recommendation from a stratified medicine trial. For example, it is possible that both biomarker-stratified groups could derive benefit from the new intervention and, even though one group could derive statistically more benefit than the other, the intervention would still be recommended for all patients rather than taking a stratified approach (see scenario A in Table 8). However, under scenarios B and C in Table 8, it would be advisable to assess the extent of power available to test for an interaction between the biomarker and intervention.
| Scenario | Biomarker-positive group | Biomarker-negative group | Potential conclusions from the trial | |
|---|---|---|---|---|
| Prevalence = X%; control group event proportion = E1 | Prevalence = 100 – X%; control group event proportion = E2 | Is a stratified medicine approach recommended? | Is the new treatment recommended? | |
| A | ≥ δ1 observed | ≥ δ2 observed | No | Yes to all |
| B | ≥ δ1 observed | < δ2 observed | Yes | Only to the biomarker-positive group |
| C | < δ1 observed < δ1 | ≥ δ2 observed | Yes | Only to the biomarker-negative group |
| D | < δ1 observed | < δ2 observed | No | No to all |
Deciding whether or not to power for a significant test of interaction is dependent on how strongly the investigators feel that the biomarker groups can be treated as separate populations or if they are inherently one population. Some suggested methods for determining sample size for interaction are described in the literature. 230–233
Parameters to consider
Table 7 in Appendix 3 presents the parameters that are required (in addition to specification of significance level and statistical power) when determining sample sizes for a stratified medicine study. For simplicity, we consider a binary biomarker. For sample size calculations, investigators need to agree on reasonable values for the biomarker prevalence (X), the event proportion in the control arms of each biomarker group (E1 and E2), and the target difference required for each biomarker group (δ1 and δ2). The scenarios in Table 8 provide a guide on how the trial may be interpreted depending on the treatment effects observed in each biomarker group. Ideally, the evidence on which these conclusions are drawn would be based on adequately powered tests of interaction. The selection of δ1 and δ2 are challenging, as is the case with specifying any target difference. The choice is often complicated by other considerations based on secondary outcomes, such as side effects or high costs associated with the new treatment. This is particularly true in oncology, where these designs are most commonly used. δ2 may be selected on the basis of a difference below which the treatment would not be recommended, which could be close to the value under the null hypothesis.
Adaptive designs
Adaptive designs for clinical trials234 enable the analysis of data as they accumulate during a trial at one or more interim analyses, with the results of these analyses used to modify the trial design in some way. A wide range of design adaptations have been suggested, but perhaps the most common involve either early stopping if the intervention under investigation appears particularly promising or particularly unpromising, or a change in the planned sample size based on early estimates of nuisance parameters or treatment effects. Such designs are considered appealing because of the opportunities they give for increasing flexibility and efficiency. A recent and extensive summary of methodology in the area is given by Wassmer and Brannath. 235
Like almost all confirmatory RCTs, trials with an adaptive design are usually designed to have a fixed type I error rate and power for some specified target difference. The increased flexibility afforded by an adaptive design can, however, have implications for the choice of the target difference used in the construction of the design. In a conventional trial, there is often a compromise between ensuring the trial has sufficient power to detect a small clinically meaningful difference and minimising the sample size if a larger treatment difference is anticipated or hoped for. With an adaptive design, the final sample size can depend on the observed interim data. It can thus be possible to design the study to ensure that statistical power is maintained to detect a small difference, but to also allow the trial to stop with a smaller sample size if a larger treatment difference is observed. In a similar way, if there is uncertainty regarding the SD of the primary outcome at the planning stage, the final sample size can be adjusted depending on interim data, to maintain power for a target difference specified on an absolute scale when this is considered desirable.
Much recent interest in adaptive designs for clinical trials has focused on multiarm, multistage236,237 trial designs, in which more than one experimental treatment is initially compared with a control arm. Less effective treatments are then dropped as the trial progresses. In this case, issues relevant to the specification of target differences in multiarm studies, as described in Appendix 3, Methods for specifying the target difference, should also be considered.
Glossary
- Estimand
- The intended effect to be estimated to address a trial objective. It can be defined in terms of the population of interest; the outcome measure; how intercurrent events (those which preclude observation of the outcome or potentially affect its measurement, e.g. death or participant withdrawal from the study) are dealt with; and how the outcome is expressed (e.g. mean difference).
- Important difference
- A difference in an outcome that is considered to be important to one or more stakeholder groups (e.g. patients).
- Minimum clinically detectable change/difference
- The smallest value that is judged to be detectable in the sense that it is greater than the measurement error of a specific observation. It is premised on the rationale that a difference smaller than this is not likely to be important. Most commonly, such an approach is used for quality-of-life measures, in which case the construct of interest cannot be directly measured. As such, this approach only indirectly addresses the issue of importance of a particular difference. The adjective ‘clinically’ is used here to differentiate it from a minimum statistically detectable change/difference. Accordingly, although the shortened abbreviation ‘MDC/D’ (minimum detectable change/difference) is often used in the literature, here ‘MCDC/D’ (minimum clinically detectable change/difference) is used to differentiate it. There are minor variants in the terminology, such as using minimal instead of minimum and the exact definition.
- Minimum (clinically) important change/difference
- The smallest value that is judged to be important. The adjective ‘clinically’ is often added to refer to the context of medical care. In shortened form, the abbreviation ‘MCID’ (minimum clinically important difference) is probably most often used in the literature. Minor variants of the term, such as minimal instead of minimum, are commonplace. The use of the word ‘change’ instead of ‘difference’ implies it was premised on a within-person change (e.g. from before to after treatment).
- Minimum statistically detectable change/difference
- The smallest value that is expected to be statistically detectable at the prespecified type I error rate. If the required sample size is achieved, the target difference is one that can reasonably be expected to be statistically detected should it exist. It is not, however, the only value, nor the smallest value, that could lead to a statistically significant change or difference. The latter is the minimum statistically detectable change/difference. The adjective ‘statistically’ is used here to differentiate it from a minimum clinically detectable change/difference. Although the shortened abbreviation ‘MDC/D’ (minimum detectable change/difference) is often used in the literature.
- Statistical power
- The probability that, for the given assumptions, the statistical analysis would correctly detect a given difference and produce a statistically significant result. It is the complement of the probability of a type II error (i.e. the probability of a type II error not occurring). A power level of 80% or 90% is commonly considered acceptable, although the choice is arbitrary.
- Target difference
- The value that is used in the sample size calculation of a randomised trial that expresses the difference between the intervention groups that is sought to be detected. There are no theoretical constraints on its value beyond those imposed by the outcome and the planned analysis. For example, the proportion of participants with an adverse event can range from 0 to 1.0. A target difference may or may not be one that could be considered important and/or realistic.
- Type I error
- The probability of falsely rejecting the null hypothesis (typically the null hypothesis is usually that there is no difference between the treatments) and concluding the alternative hypothesis (corresponding, typically, that there is a difference between the treatments). The type I error is typically set to the 0.05 level; this level is then applied to a statistical analysis to infer the occurrence or not of a statistically significant finding.
- Type II error
- The probability of failing to reject the null hypothesis (typically that there is no difference) when there is a real difference between interventions.
List of abbreviations
- A&F
- audit and feedback
- ACL
- anterior cruciate ligament
- ACL-SNNAP
- ACL Surgery Necessity in Non Acute Patients
- CACE
- complier-average causal effect
- CI
- confidence interval
- CONSORT
- Consolidated Standards of Reporting Trials
- CRS
- chronic rhinosinusitis
- CRUK
- Cancer Research UK
- CTU
- clinical trials unit
- CV
- coefficient of variation
- DELTA
- Difference ELicitation in TriAls
- HR
- hazard ratio
- HTMR
- Hubs for Trials Methodology Research
- ICC
- intracluster correlation
- INB
- incremental net benefit
- ITT
- intention to treat
- JSM
- Joint Statistical Meetings
- KOOS
- Knee injury and Osteoarthritis Outcome Score
- MACRO
- Management for Adults with Chronic RhinOsinusitis
- MAPS
- Men After Prostate Surgery
- MCDC
- minimum clinically detectable change
- MCID
- minimum clinically important difference
- MET
- medical expulsive therapy
- MID
- minimum important difference
- MRC
- Medical Research Council
- NIH
- National Institutes of Health
- NIHR
- National Institute for Health Research
- OPTION-DM
- Optimal Pathway for TreatIng neurOpathic paiN in Diabetes Mellitus
- OR
- odds ratio
- PICOT
- population, intervention, control, outcome and time frame
- PPI
- patient and public involvement
- PSI
- Statisticians in the Pharmaceutical Industry
- RAPiD
- Reducing Antibiotic Prescribing in Dentistry
- RCT
- randomised controlled trial
- RDS
- Research Design Service
- RR
- risk ratio
- SCT
- Society for Clinical Trials
- SD
- standard deviation
- SES
- standardised effect size
- SNOT-22
- Sinonasal Outcome Test – 22 items
- SUSPEND
- Spontaneous Urinary Stone Passage ENabled by Drugs
