Notes
Article history
The research reported in this issue of the journal was funded by the HTA programme as project number 15/141/09. The contractual start date was in September 2014. The draft report began editorial review in May 2019 and was accepted for publication in November 2019. The authors have been wholly responsible for all data collection, analysis and interpretation, and for writing up their work. The HTA editors and publisher have tried to ensure the accuracy of the authors’ report and would like to thank the reviewers for their constructive comments on the draft document. However, they do not accept liability for damages or losses arising from material published in this report.
Declared competing interests of authors
none
Permissions
Copyright statement
© Queen’s Printer and Controller of HMSO 2020. This work was produced by Hernández Alava et al. under the terms of a commissioning contract issued by the Secretary of State for Health and Social Care. This issue may be freely reproduced for the purposes of private research and study and extracts (or indeed, the full report) may be included in professional journals provided that suitable acknowledgement is made and the reproduction is not associated with any form of advertising. Applications for commercial reproduction should be addressed to: NIHR Journals Library, National Institute for Health Research, Evaluation, Trials and Studies Coordinating Centre, Alpha House, University of Southampton Science Park, Southampton SO16 7NS, UK.
2020 Queen’s Printer and Controller of HMSO
Chapter 1 Introduction
In many health-care systems across the globe, decisions about the types of health technologies, strategies and service delivery options provided are informed by some form of economic evaluation. This entails making comparisons between competing options in terms of their costs and benefits. The type of economic evaluation in most widespread use is referred to as cost-effectiveness analysis (CEA). In particular, health benefits are expressed as quality-adjusted life-years (QALYs). The QALY is a metric that combines concerns for both length of life and quality of life into a single numeraire. It does so by rating health states on a scale anchored around the values of one (a year spent in full health) and zero (states equivalent to death).
The value that any specific health state can take on this scale is limited to a maximum of one, but can take negative values if it is considered to be so severe that it is deemed worse than being dead. These health state valuations, sometimes referred to as health state utilities, can be estimated using many different methods. They can also be estimated from different samples of respondents. For example, there is significant debate about whether health state utilities should reflect the values of patients with experience of the condition or the values of the general public. Each of these options leads to different valuations of health states and are important areas of research, though they are not the focus of this report.
Our aim is to present new research on a specific approach to estimating health state utilities that has become increasingly prevalent in recent years. This is the approach referred to variously as ‘mapping’, ‘cross-walking’ or ‘transfer to utility’. We use the term ‘mapping’ throughout this report.
Mapping refers to a two-stage process to estimate the utilities for the health states required for a CEA. In the first stage, the relationship between the health state utilities of interest and some set of explanatory variables is estimated using data from a sample of patients with the same clinical condition but not necessarily related to a study of the health technology that is the focus of the CEA. The explanatory variables may be some form of clinical measure, patient-reported outcome measures (PROMs) or other sociodemographic information. In the second stage, the estimated model is used to predict the health state utilities for health states required in the cost-effectiveness model.
This report provides more detail of what mapping is, how it has been performed previously and the challenges that are faced when conducting a mapping study (see Chapter 2). In Chapter 3 we introduce a series of flexible statistical methods for mapping that are designed to overcome many of these challenges. We describe how they can be used and how the results from different model types can be compared in a meaningful way. Chapter 4 presents results from a series of case studies that test and compare the performance of different mapping models as well as a separate case study of the specific case of mapping between two preference-based measures (PBMs). In Chapter 5 we present some preliminary analyses on a number of methodological issues that we have identified in the course of our research. Finally, we summarise our overall findings and provide recommendations for future research based on those findings in Chapter 6.
Chapter 2 Background
Preference-based measures
To calculate QALYs, there is a requirement not only to describe the impact of health technologies on quality of life but also for that quality of life to be valued on the appropriate scale, that is, based on the preferences of an appropriate sample and anchored around the values of one for full health and zero for states equivalent to being dead.
One option for achieving this is to ask patients with the condition in question and experiencing the health states that are relevant to the CEA to value their own health. The main methods for undertaking such valuations take the form of thought experiments and are known as time trade-off (TTO) and standard gamble (SG), though a range of other valuation methods can also be used, sometimes in combination. TTO requires respondents to indicate the length of life in full health that they would consider equivalent to some other length of life in their impaired state. They are therefore asked to directly trade off length of life for improved quality of life. SG asks respondents to trade off uncertainty (between full health and death) for health. Specifically, respondents are asked to choose between a certain option in impaired health and an option associated with a return to full health with probability p, but also a risk of death with probability 1 – p.
However, these approaches are time-consuming to administer, relatively costly and place a substantial burden on both study participants and researchers. In the context of a clinical study, these approaches would often be considered not feasible. In addition to these practical constraints on direct utility elicitation, the prevailing view of most health technology assessment (HTA) agencies is that the preferences of the general public, rather than of patients only, are those most appropriate for informing investment decisions in a publicly funded health-care system. Instead of obtaining values directly from patients, the values for health states that are then used to calculate QALYs predominantly come from generic PBMs, which are based on the preferences of some sample of the general public.
Most PBMs are intended to be applicable to a wide range of different disease areas and health technologies and hence are termed ‘generic’. These measures have become core features of the standard approach to measuring and valuing health and key inputs to the calculation of QALYs. A PBM comprises two elements: a survey instrument that is used to describe health and a valuation set that provides an ‘off-the-shelf’ set of values for each of the health states that can be described by the survey instrument. These sets of values have been calculated using methods consistent with economic theory, such as TTO and SG, in large scale samples of the general population. Thus, the practical difficulties associated with the administration of these methods in patient samples are avoided.
Several such generic PBM instruments have been developed. The most widely used examples are the EuroQoL-5 Dimensions (EQ-5D),1 of which there are two main versions [the EuroQoL-5 Dimensions, three-level version (EQ-5D-3L), and the EuroQoL-5 Dimensions, five-level version (EQ-5D-5L)]; the Short Form questionnaire-6 Dimensions (SF-6D),2 which is based on the Short Form questionnaire-36 items (SF-36);3 and the eight-dimensional Health Utility Index Mark 3 (HUI3). 4 Table 1 summarises these example measures.
| Instrument | Dimensions | Levels | Number of health states | Valuation method | Range of health utilitiesa |
|---|---|---|---|---|---|
| EQ-5D-3L | Five dimensions: mobility, self-care, usual activities, pain/discomfort and anxiety/depression | Three levels: no/some/extreme problems | 243 | TTO | –0.594 to 1 |
| EQ-5D-5L | Five dimensions: mobility, self-care, usual activities, pain/discomfort and anxiety/depression | Five levels: no/slight/moderate/severe/extreme problems | 3125 | TTO/DCE | –0.285 to 1 |
| SF-6D | Six dimensions: physical functioning, role limitations, social functioning, pain, mental health and vitality | Between four and six levels in each dimension | 18,000 | SG | 0.301 to 1 |
| HUI3 | Eight dimensions: vision, hearing, speech, ambulation, dexterity, emotion, cognition and pain | Between five and six levels in each dimension | 972,000 | SG and VAS | –0.359 to 1 |
Both the health classification systems and the response samples and analytical methods that underpin the valuation sets differ for each of these PBMs. Effectively, this means that PBMs cannot be treated as if they were interchangeable: they do not generate the same values for the same health states. 9–14 This has important implications for policy-makers seeking consistency across the health-care allocation decisions they are required to make.
The EQ-5D-3L is one of the most widely used PBMs and can be used to illustrate how PBMs are constructed and used. Its descriptive system comprises five dimensions: mobility, self-care, usual activities, pain/discomfort and anxiety/depression. Respondents are asked to indicate their health status on each dimension at one of three levels: no problems, some problems and extreme problems. In total, 243 different health states can be specified by this descriptive system. 5 In the UK, the values attached to these health states range from –0.594 for the worst health state (extreme problems in all dimensions) to 1 for full health (no problems in any dimension). Values for 42 of the 243 health states were elicited using TTO from a final sample of 3395 UK members of the general public. 5 To obtain values for all health states described by the EQ-5D-3L, a regression model was used on these data to estimate the value of all 243 health states.
Many jurisdictions recommend the use of PBMs for economic evaluation, such as those of England and Wales,15 Spain,16 France,17 Thailand,18 Finland,19 Sweden,20 Poland,21 New Zealand,22 Canada,23 Colombia24 and the Netherlands. 25 Some recommend the use of a specific instrument, usually the EQ-5D. 26
To use PBMs to facilitate the estimation of QALYs for CEA, the ideal situation in many cases would see the PBM administered to patients as a PROM, at multiple time points, in clinical studies of the health technology of interest. The patient responses to the descriptive system of the PBM would then be attached to the pre-existing, off-the-shelf values by the analyst, who would calculate the health gain, in QALY terms, associated with the health technology compared with the alternative treatment in the clinical study.
However, there are many settings where either this ideal situation does not exist or it is insufficient for the needs of the economic analysis. First, there may have been no PBM administered as part of the relevant clinical studies. PBMs are largely required for the economic analysis, yet in many situations the design of clinical studies focuses exclusively on establishing clinical effectiveness. Although HTA agencies may increasingly encourage the use of PBMs, the impact of this varies and it is only one of many different considerations for those funding and designing clinical studies. Second, there may have been a PBM administered in the relevant clinical studies but it is not the one that is recommended for the jurisdiction in which the economic evaluation is to be undertaken. This frequently occurs in cases of multinational clinical studies in which decisions about which PBM may be taken is based on judgements about the needs of the countries in which the clinical study is taking place, or commercial judgements about the most important markets. It can also be the case that, as new versions of PBMs are developed, the HTA agency recommendations change. Third, although the appropriate PBM may have been administered in clinical studies, this may be insufficient for the needs of the economic evaluation. Often, economic models are required to extrapolate the differences in costs and benefits beyond the limited time horizon of the clinical study, and/or to different populations. There may be several studies that need to be combined, and multiple comparators not included in the key studies need to be modelled. The clinical studies may not provide sufficiently large patient samples, patients may be healthier than patients in real clinical practice and there may be few observations of rare but important adverse events of disease complications. All of these factors mean that there is insufficient information on health utilities from the clinical studies.
In all of these cases there is a deficiency in the evidence base that makes it insufficient to furnish the requirements of the economic evaluation. ‘Mapping’ is one method that can be used to try to overcome this deficiency.
Mapping: what is it and why is it used?
Mapping, also referred to as ‘cross-walking’ or ‘transfer to utility’,27 is a method used to predict what the value of a health state would have been, perhaps conditional on many other factors, had it been recorded directly with the PBM of choice. Mapping requires the identification of a suitable external reference data set (meaning a different data set to the clinical studies that are deficient in some way) that contains both the PBM required for the economic evaluation and the measure(s) that have been used in the clinical study or that otherwise define the health states of interest.
The data from the mapping data set can then be used to estimate the relationship between the PBM and the clinical outcome measures, thereby providing the means to bridge the gap between the evidence available in the clinical studies and the requirements of the economic evaluation. The mapping is used to impute the utility of health states from non-utility-based information about those health states. Note that the mapping data set does not need to be from a study of the technology in question, nor does it need to be derived from a randomised clinical study, because the mapping estimation itself does not entail the estimation of a treatment effect.
The estimated statistical relationship may then be used to infer the missing PBM in the clinical study so that it can be incorporated in the economic evaluation. If y denotes health utility and x the vector of conditioning variables used in the mapping model (for example, the clinical outcome measure age or gender), the estimated mapping model gives us an estimate of the conditional distribution of the utilities, f(y|x). We can use the mapping model to do either of the below:
-
Simulate the distribution of utilities across patients using the full conditional distribution, f(y|x). This use could be appropriate for a patient-based simulation model, or an economic evaluation alongside a clinical trial, where the analyst needs to use the full distribution of patient utilities.
-
Predict the missing utility using the conditional expectation, E(y|x), as would be required for a typical cohort-based decision model.
These two alternative uses of the mapping model are related to important concepts often confused in the mapping literature. The unconditional distribution of utilities across patients, f(y), describes the distribution of health state utilities. This distribution is bounded at the top by one, the value of full health, and at the bottom by the lowest utility value for the particular instrument used (see Table 1). For a given set of conditioning variables, x = X, the conditional distribution, f(y|X), describes the distribution of utilities in the subpopulation of patients for whom the conditioning variables take the combination of values X; individuals with the same observable characteristics X differ in their observed utilities owing to an unobserved random component. The conditional expectation, E(y|X), is the mean of the conditional distribution, f(y|X); individuals with the same observable characteristics X share the same mean. Therefore, the variation in the distribution of the conditional means, E(y|X), is due to the variation in the combinations of values X in the population of interest. The conditional distribution, f(y|x), includes, in addition, the unexplained variation of utility around the conditional means. Hence, the distribution of the conditional means differs from the conditional distribution. In particular, the distribution of the conditional means will always have less variation than the conditional distribution. 28 We outline this issue in more detail in Chapter 3, Predictions: mean versus distribution. It is worth noting at this point that estimating the entire conditional probability structure, f(y|X), has the advantage of allowing the mapping model to be used for both (1) and (2) above, as the conditional means can be derived from it.
Mapping is in widespread use in HTA. A database of mapping studies updated in 2019 [Health Economics Research Centre (HERC) database of mapping studies]29 contains 182 published studies. Many more are undertaken for specific economic evaluations but are never separately published. A review of 79 National Institute for Health and Care Excellence (NICE) appraisals in 201330 found that 22% were reliant on mapping, either from published sources or mapping estimated specifically for the appraisal.
Mapping is an area in which guidance on some specific areas of good practice has been published, intended to reflect existing research evidence31,32 or provide recommendations on reporting standards. 33
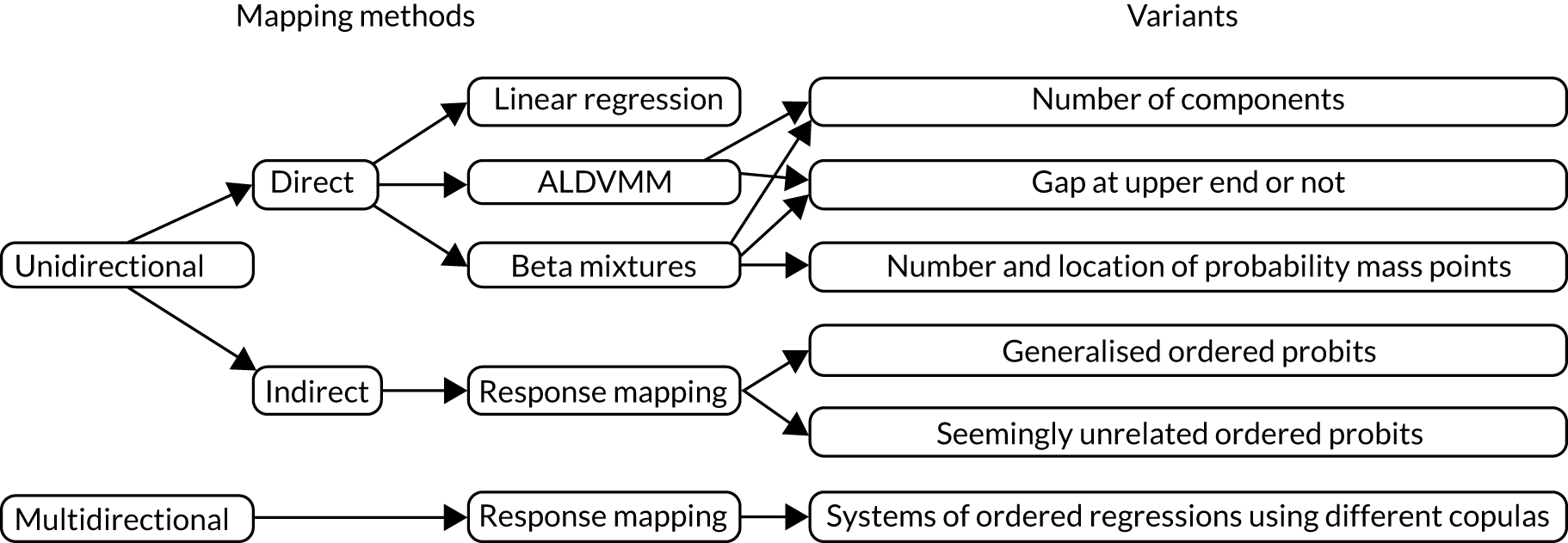
Overview of different mapping approaches
There is a longer history of studies examining alternative statistical models for cost data in the published literature than health utility data. 34,35 Cost data are characterised by non-negative values, heteroscedasticity and high kurtosis because of large proportions of respondents incurring zero costs (the lower limit). Much less attention has been given to the challenges associated with modelling health utility data until more recently. This is surprising for two reasons. First, the challenges associated with utility data are more numerous than those associated with costs. Second, the incremental benefits appear in the denominator of the incremental cost-effectiveness ratio (ICER) and are typically very small, such that apparently trivial changes arising from differences in estimation methods often lead to far from trivial differences in estimates of cost-effectiveness.
In general terms, there are two types of methods for mapping. The first is a one-step process that models the health utility values directly. Although potentially simpler, this means that the resultant mapping model is specific to the value set for which the model was estimated; it cannot be used for other countries where a different value set is relevant. This approach also discards the more detailed information contained in the responses to the individual dimensions. In some cases, this information may be quite useful.
The second set of mapping methods can be labelled as indirect mapping approaches (also referred to as ‘response mapping’), which use a two-step process. In the first step, the discrete responses to the descriptive system of the instrument are modelled. For example, in cases in which the EQ-5D-3L is the target of the mapping model, five (typically independent) discrete data models (such as ordered probits/logits, multinomial logits) are used. The models estimate the probability of the health state of the individual being at levels one, two and three for each dimension in the descriptive system. Once these models have been estimated, they can be used to calculate the expected health utility as a second, separate step, using the estimated distribution of responses together with a value set. Because it is only the second step that is value-set specific, the same first-stage mapping model can be used for any country. However, the indirect approach also needs enough responses at all levels in each dimension, otherwise the mapping model is unable to predict a full conditional probability distribution across all health states. Mappings to PBMs with a larger number of levels in each dimension are more likely to encounter this problem. 36,37
Direct methods
Modelling health utilities directly is not straightforward because such data are characterised by several challenging features. Health utility data are bounded: limited at the top at one (the value of full health) and at the bottom by the value of the worst health state described by the instrument. The location of this lower boundary differs by PBM and by the country-specific value set, but they all must have a lower bound (see Table 1). Most data sets exhibit a significant mass of observations at the upper boundary of one, immediately followed below by a relatively large gap in the distribution before the next feasible utility value. The rest of the distribution is usually characterised by multimodality and/or skewness. The degree to which these features are apparent varies by instrument, disease area and patient sample severity.
Given these distributional features, it is perhaps surprising to find the widespread use of linear regression for mapping. The HERC database29 reports the first identified mapping study as using a linear regression for modelling the relationship between EQ-5D-3L and other disease-specific outcome measures in a sample of patients with rheumatoid arthritis (RA). 38 Linear regressions are the most commonly used direct mapping model, usually estimated using ordinary least squares (OLS), with a smaller number of more recent studies using robust MM estimators (the MM estimators is a class of robust estimators for the linear model introduced by Yohai39). A recent systematic review of mapping studies to PBMs found that linear regression estimated using OLS was still the most common approach, used at least 75% of the time in each of the PBMs covered in the review. 40
Modelling PBMs using a linear regression is problematic because of the features that are typical of health utility data.
The first issue, which has received surprisingly little attention in this area, relates to the bounded nature of PBMs. Linear regression is built on the assumption that the regression function is linear. In other words, the expected value of health utility, conditional on a predictor variable, looks like a straight line when plotted against the value of the predictor variable. Figure 1 shows why that linearity assumption causes problems for regression prediction. As health utility can never exceed one, its expected value conditional on the predictor x can also never exceed one. It will generally lie below one and approach it as an asymptote as x increases (assuming x and y are positively related). Thus, the true regression relationship (the solid red line in Figure 1) must be non-linear in general. Mistakenly fitting a straight line (the dashed blue line in Figure 1) then tends to overpredict health utility for cases with health utility likely to be at or close to one. Linear regression will also tend to underpredict health utility in cases of very poor health, because the slope of the regression line is too large.
FIGURE 1.
Example of incorrect prediction by misspecified linear regression for health utilities limited at 1.
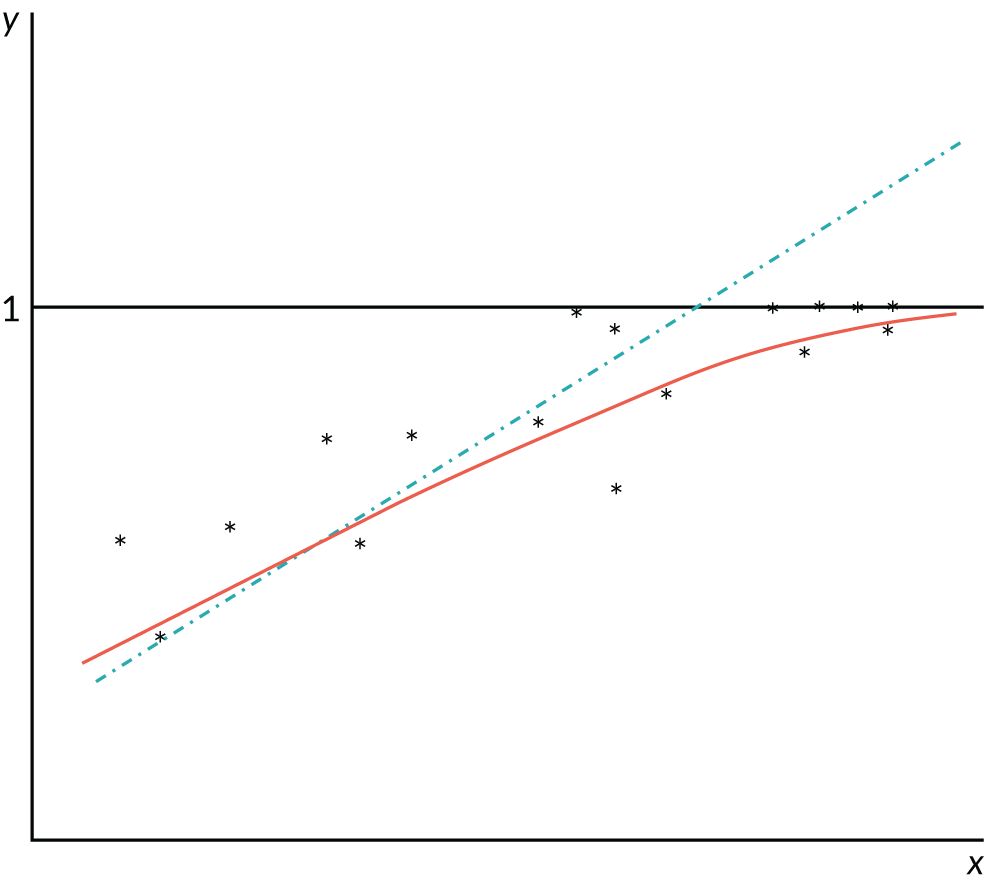
A possible response to this problem would be to use non-linear regression – in other words, fit a curve like the solid curve (solid red line) in Figure 1. This type of regression is robust in the sense that it gives approximately unbiased estimates even if the usual assumption of normally distributed and constant-variance residuals are invalid. Unbiasedness requires that the non-linear form fitted is linear in parameters; if this is not so, the non-linear regression estimator is consistent rather than unbiased, and gives good results in large samples (subject to mild regularity conditions). However, some of the standard inferences about the model [hypothesis tests, confidence intervals (CIs), etc.] will be invalid unless the constant-variance (homoskedasticity) assumption is correct. Unfortunately, a limited dependent variable model cannot have a constant residual variance: as the regression curve approaches the ceiling of one, the variance must decline towards zero, as illustrated in Figure 1. In any case, even if homoskedasticity were a tenable assumption, standard tests and CI formulas may be poor approximations in small samples, given the non-normal features of skewness, discontinuity and multimodality that characterise health utility data.
Published evidence repeatedly demonstrates the poor performance of the linear regression. Most studies illustrate this with reference to the conditional means and show that the models tend to understimate mean health utility at the upper end of the distribution, where patients are in good health, and overestimate it at the bottom end, where patients are in poorer health as expected given the discussion above. Chapter 3, Model comparisons, illustrates with an example the type of systematic underpredictions and overpredictions that one is likely to see when using linear regressions as opposed to other models that can account for all of the features of the data.
In cost-effectiveness models that assess the value of clinically-effective treatments, the use of these mapping models will bias results. They tend to underestimate the true value of health gain, resulting in lower QALYs and higher cost-effectiveness ratios. Even though the magnitude of the bias seems small, it is large relative to the range of PBMs, and, in economic models, those biases accumulate over the individual’s lifetime. Furthermore, cost-effectiveness ratios are unstable quantities usually portraying large numbers on the numerator divided by very small numbers. Small changes to the denominator typically result in large changes in the cost-effectiveness ratio that have the potential to change reimbursement decisions solely because of the mapping model used. 41 Alternative models have been considered, on the basis that they may be more suitable to some aspects of the utility distibution. For example, tobit, censored least absolute deviation and two-part models had been used in the literature to capture the large proportion of observations at full health.
The use of the tobit model in mapping has been subject to discussion in published literature in relation to its potential appropriateness or otherwise for health utility data. In particular, it has been argued that the tobit model is inappropriate for modelling health utility data because it is designed for the analysis of censored data: health utility data are not censored because values of health > 1 are not possible. 42 This criticism stems from an apparent confusion between two different applications of the tobit model that lead to the same statistical model. The tobit model can arise from true data censoring where the variable of interest is not fully observed. It is in the context of data censoring that the tobit model is most typically used in economics at present. A typical example of this is modelling data on income using data from surveys that, to encourage responses at higher levels of income, use an upper limit above which respondents need to indicate only if their income is above that limit. The data are thus observed to lie within a particular range only, which causes a pile-up of observations in that category. However, the variable of interest is still underlying income. The same tobit model can also arise from a corner solution of choice, as in Tobin’s original article. 43 Tobin developed his original model to deal with variables that are limited, not censored, such as expenditure on durable goods. Expenditure can only be positive or zero, and the variable is referred to as limited at zero. At very disaggregated levels of expenditure or for luxury goods, pile-ups at the ‘corner’ of zero are likely. There is no censoring in this case; the entire range of the variable is observed. In fact, the word ‘censored’ is completely absent from Tobin’s original paper. Health utility data are analogous to this second case. The variable of interest is the actual response variable and the pile-up at one represents a corner solution. This distinction is important for prediction purposes. The linear prediction is appropriate if the pile-up is due to censoring, but the (non-linear) prediction of the response variable should be used in the case of a corner solution.
The range of alternative methods, including the use of the tobit model, have tended to not improve over the poor fit of the linear regression. This is because these methods address only some of the challenging distributional features of health utility data. Only models that are able to address all features are true contenders for a properly specified mapping model. Worryingly, this has led to a widespread claim that mapping is fundamentally unreliable. 44 This belief has been shown to be misguided with the application of more flexible statistical methods in many studies. Austin and Escobar45 proposed the use of finite mixture models to estimate PBMs and applied it to the HUI3. Mixtures of normal distributions are very flexible and can approximate functional forms that are difficult to model using a single distribution. Their use is often linked to the presence of multimodality, but they can also approximate unimodal, highly skewed or kurtotic distributions. Austin and Escobar45 use a degenerate normal distribution with a mean of one and a very small standard deviation to account for the mass of observations at one. Mixtures of normal distributions have been used to model other PBMs, such as the EQ-5D-3L,46–49 SF-6D46 and HUI3. 48 Hernández Alava et al. 50 introduced a finite mixture model specifically developed to deal with the idiosyncrasies of EQ-5D-3L data. The model is based on underlying distributions analogous to the tobit model (corner solution), extended to allow for the gap between one and the immediately previous value encountered in health utility data. The model has been applied successfully to different disease areas51–54 as well as different PBMs. 37
Simultaneously, a separate strand of the methodological literature introduced the use of beta distributions. Beta distributions are very useful for modelling health utilities data because they are bounded and are able to accommodate a number of different shapes. Similarly, fractional response models are very useful in modelling bounded data, but, unlike models based on beta distributions, provide only estimates of the conditional means, not the conditional distribution of utilities. Basu and Manca55 proposed the use of two-part beta regressions to account for bounded data, skewness and the spike of observations at the value of full health. Some studies have suggested that beta regression is not appropriate in cases where the PBM displays negative values56 and, in some cases, researchers have converted all negative values to zero ad hoc purely for convenience,57,58 inadvertently creating a potential problem given the sensitivity of beta regressions to observations at the boundaries. Standard transformations exist and are regularly used with beta regressions in other applications. 59 The beta regression approach has been extended to the use of mixtures. 47 The development of methods based on beta mixtures is described further in Chapter 3, Flexible modelling methods for mapping, Direct methods: the beta mixture model.
Indirect methods
Fewer applications of indirect methods have been documented, which may be because of the requirement for data that spans all response categories. The first reported indirect mapping model we are aware of comprised a set of independent multinomial logit models. 60 Gray et al. 61 also estimated a set of independent logit models and coined the term ‘response mapping’, which has been adopted more widely. This approach reflects the two-stage data generating process of health state data: it separates the modelling of the responses that individuals give using the descriptive system of a quality of life instrument from the valuations of those health states.
Response mapping methods have been developed to use models that reflect the ordered nature of the response data using ordered probits/logits and generalised ordered probits. 51,53,62 Others relax the independence assumption through the use of multivariate ordered probits. 63 The multivariate model was shown to outperform competing independent dimensions models and set the ground for future avenues of research in the indirect mapping literature. However, estimating models involving high-dimensional ordinal variables remains an onerous task. The development of methods based on response mapping is described in Chapter 3, Flexible modelling methods for mapping, Indirect methods: systems of ordinal regressions using copulas.
Chapter 3 Development of methods for mapping
The characteristics of PBM data (bounded, with large numbers of observations at one boundary; non-standard distributions with gaps) as well as the small number of covariates often available for statistical modelling mean that flexible models are often required to avoid biases in the parameter estimates. This chapter summarises some of the methodological developments achieved during this project, concentrating specifically on the development of appropriate models for mapping and examining issues around model comparisons. Additional methodological developments are left to Chapter 5, in which a number of issues not directly related to model development are presented.
Flexible modelling methods for mapping describes two new flexible statistical models. Although they have been developed specifically for mapping, they can be applied outside this area in cases in which flexible models are needed. Predictions: mean versus distribution clarifies concepts often confused in the mapping literature and that have sometimes been used to dismiss mapping as a useful approach. These concepts are not exclusive to mapping; they apply equally to any statistical model. Model comparisons presents some graphical approaches to comparing mapping models to aid model selection. The advantage of these graphical approaches is that they have been designed with awareness of the role of mapping as an input into cost-effectiveness analyses.
Flexible modelling methods for mapping
Two mapping models, one based on the direct approach and one based on the indirect approach, were developed during this project to provide researchers with alternative flexible models when mapping. The direct model is based on finite mixture distributions that have already been shown to be successful in this area. It is similar to the adjusted limited dependent variable mixture model (ALDVMM),50 a model developed specifically for mapping that replaces the underlying normal distributions with beta distributions. One potential advantage of the beta distribution over the normal distribution is that its range is limited and can, therefore, easily accommodate variables such as PBMs, which have natural boundaries, although problems arise when there are large numbers of observations at those boundaries. A second potential advantage relates to the variety of shapes that it can generate with a single distribution, in contrast to the bell shape of the normal distribution. The model is briefly presented in Direct methods: the beta mixture model.
In most cases, mapping is unidirectional; we are interested in converting one measure to another, for example a disease-specific measure to a PBM, but not the other way around. The indirect model presented in this chapter (see Indirect methods: systems of ordinal regressions using copulas) has been specifically developed for cases in which the mapping model might need to be used multidirectionally. It was designed specifically for the case of mapping between two similar PBMs, EQ-5D-3L and EQ-5D-5L, but the general statistical model can be applied to other measures and extended to more than two PBMs. It is a multiequation model of ordinal regressions estimated jointly using copulas to capture the dependencies between the EQ-5D-3L and EQ-5D-5L dimensions. It also incorporates finite mixtures to allow for non-normality of the errors. The model is more challenging to estimate than unidirectional models and this complexity is not necessary for more standard uses of mapping.
Direct methods: the beta mixture model
The beta mixture model is described fully in a paper describing ,64 a Stata® versions 14 and 15 (StataCorp LP, College Station, TX, USA) community-contributed command developed to facilitate estimation of this model; its first application in the mapping literature can be found in Gray et al. 37 The following sections give some important background information about mixture models before summarising the beta mixture model.
Mixture models: background
Finite mixture models provide a very flexible statistical framework. Instead of assuming that a single distribution is enough to model a dependent variable, a number of individual component distributions are used. These distributions are mixed according to a probability structure. 65 Mixture models arise naturally when there is discrete heterogeneity in the population because the different mixture components (also known as classes) can be used to represent the different groups in the population. Although finite mixtures tend to be introduced in this context, they have another important use. Because any continuous distribution can be approximated by a finite mixture of normal densities, mixture models provide a convenient semiparametric framework to model distributional shapes that cannot be easily accommodated by standard distributions. They are parametric because each of the component distributions have a parametric form but have nonparametric features as the number of individual components is allowed to increase. Therefore, they possess a lot of the flexibility associated with nonparametric approaches as well as maintaining some of the benefits of parametric models. This flexibility is the key to their usefulness for direct modelling approaches in the mapping literature.
Mixture distributions are often used when distributions are multimodal as a way of capturing this feature, but it is important to understand that they can also approximate other features such as skewness, kurtosis and heteroscedasticity. Figure 2 illustrates the different shapes a mixture can take using a simple example of only two equal variance components. Figure 2a shows two normal components of variance equal to one. The first component has a mean of zero, the second component is located towards its right with a mean of two and they are mixed with equal probabilities. This produces a wide distribution with a flat top. Figure 2b differs in that the second component is now moved further to the right, having a mean of four. By allowing for a relatively larger separation between the components, a bimodal distribution is produced. Figures 2c and 2d depict the same two distributions used in Figures 2a and 2b respectively, but now the components are mixed with different probabilities. Component one has a probability of 0.75 and the second component a probability of 0.25. The wide and top flat distribution of Figure 2a turns into a skewed distribution in Figure 2c, whereas the bimodal distribution in Figure 2b is still bimodal but the modes have a different height in Figure 2d. An even larger number of shapes can be generated by also allowing the variances of the distributions to differ and by increasing the number of components.
FIGURE 2.
Examples of mixtures of two normal components with equal variance (σ2 = 1) and mean of the first component (µ1 = 0). (a) Mean µ2 = 2, mixing probability π = 0.5; (b) mean µ2 = 4, mixing probability π = 0.5; (c) mean µ2 = 2, mixing probabilities π1 = 0.75 and π2 = 0.25; and (d) mean µ2 = 4, mixing probabilities π1 = 0.75 and π2 = 0.25.
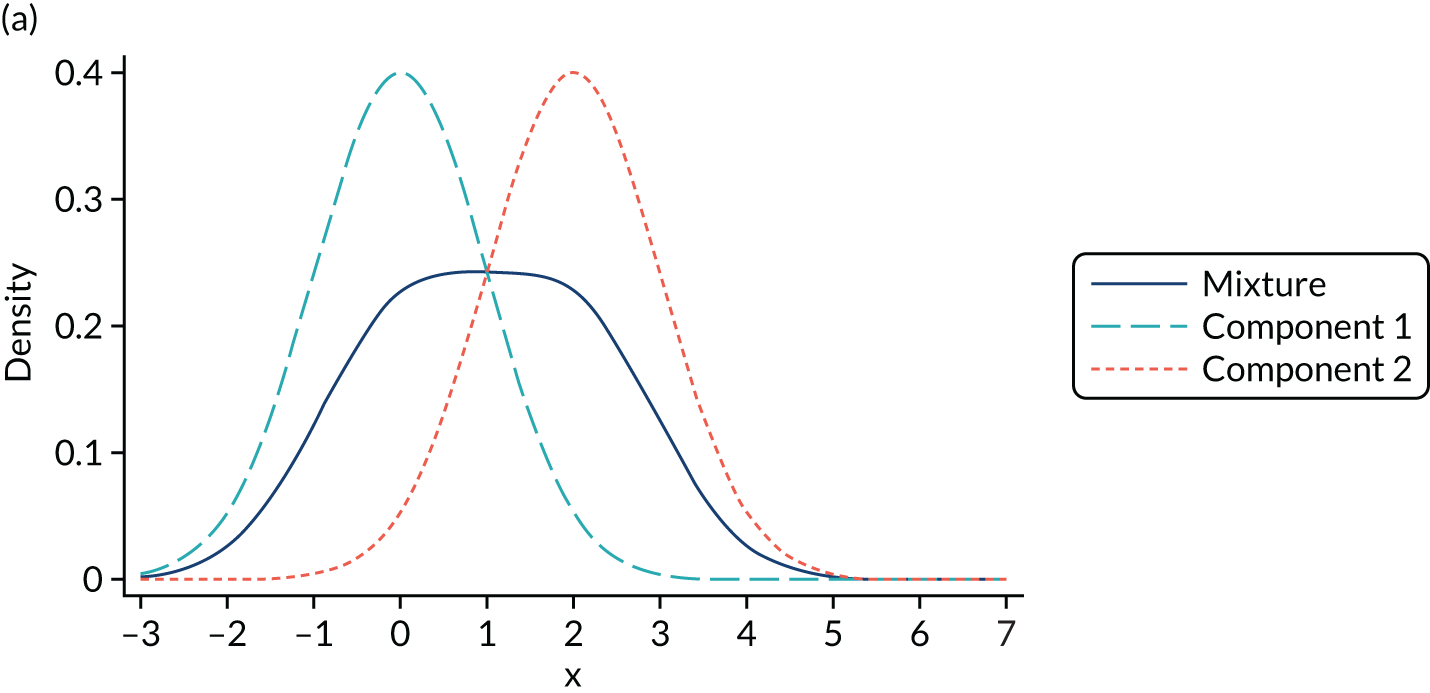
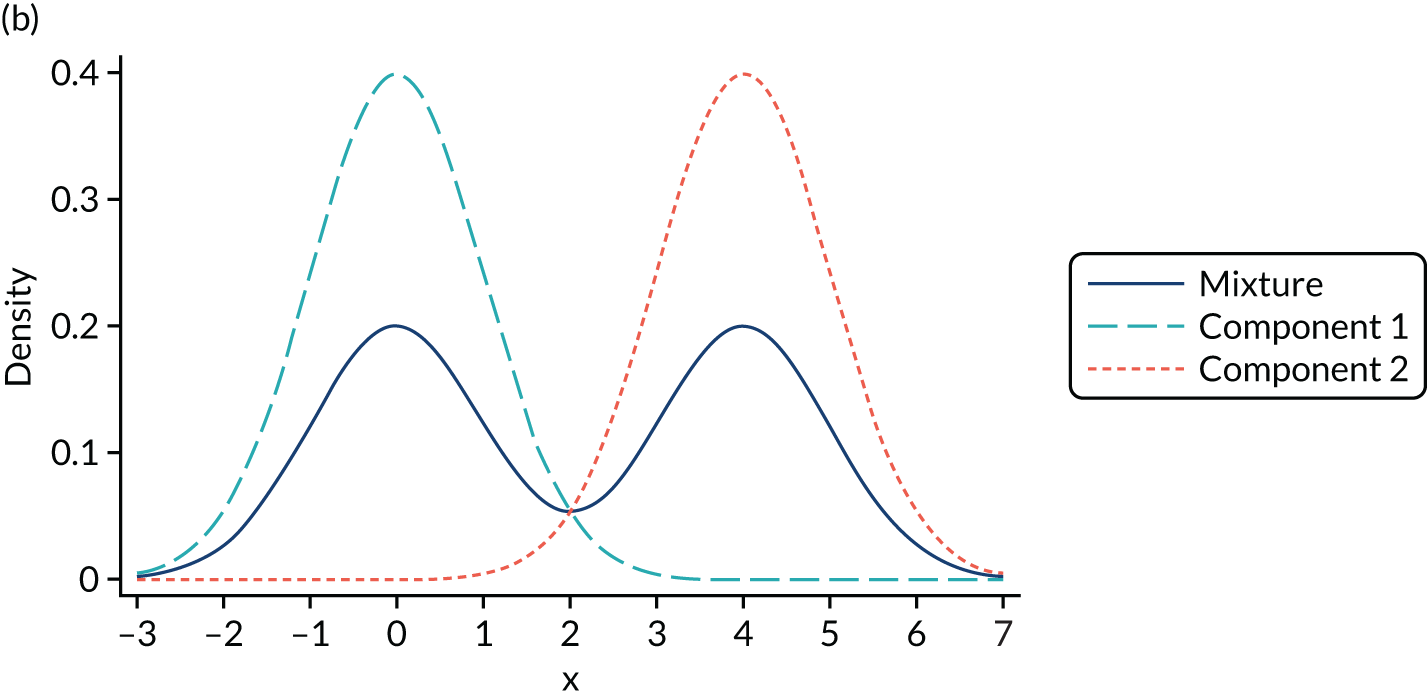
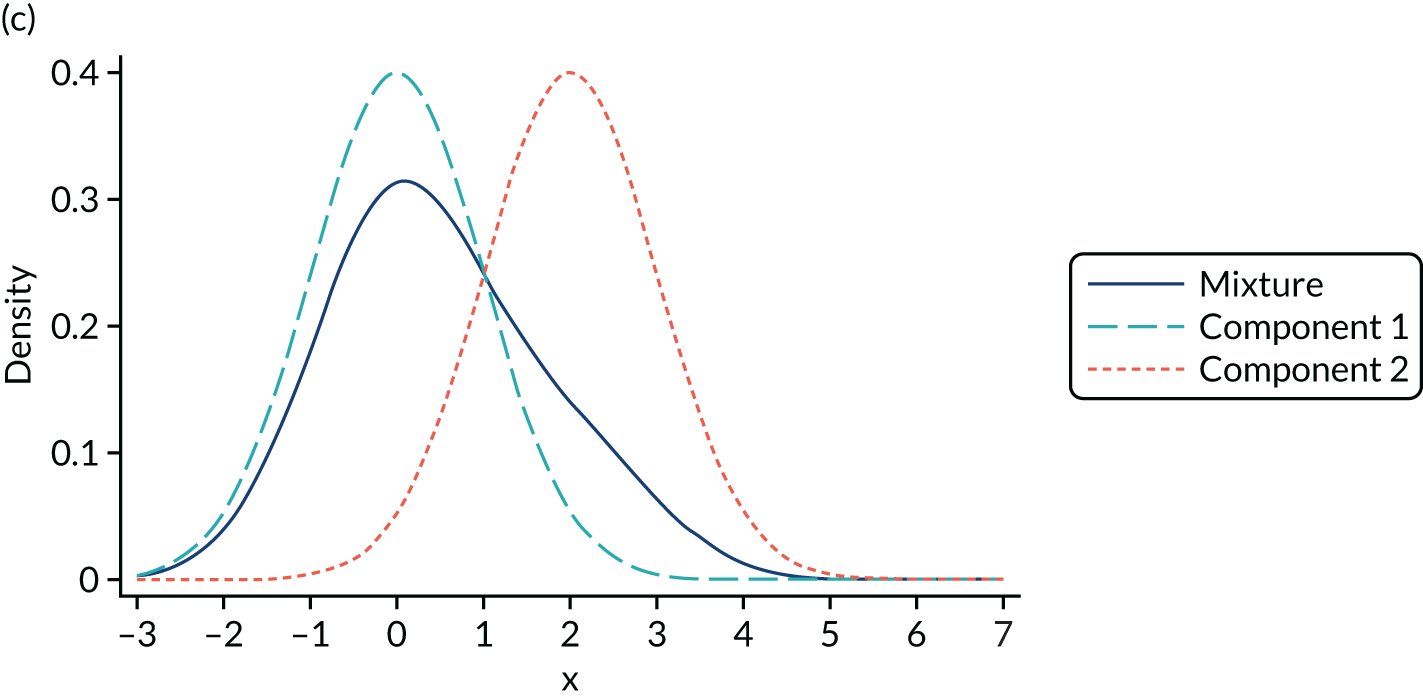
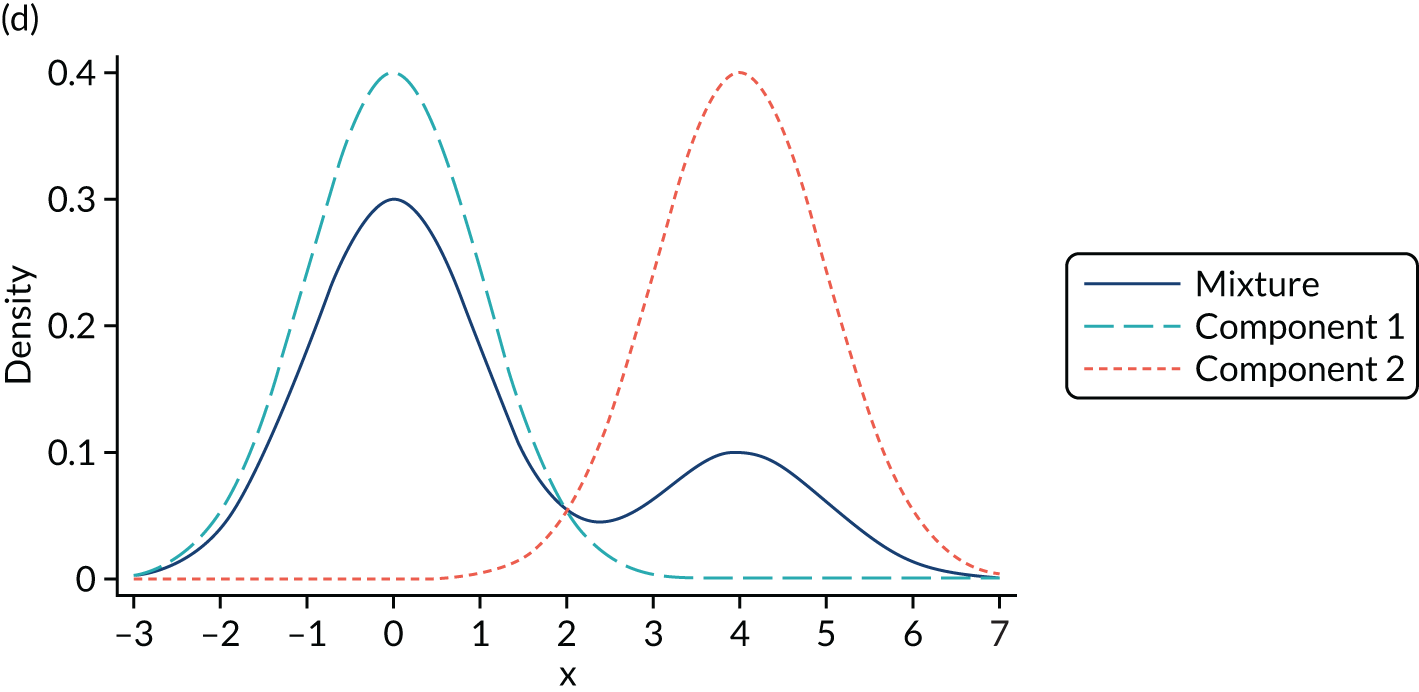
It is important to stress that the presence of two modes in a distribution does not imply that exactly two components are needed. We modelled conditional distributions, and some bimodality of the conditional distribution may be accommodated by the conditioning variables. In the case of mapping, the number of conditioning variables is typically small and, in our experience, not large enough to accommodate the extreme bimodality arising from the value set present in, for example, EQ-5D-3L UK utilities. In addition, it might be the case that more than two components are needed to accommodate a bimodal distribution if, for example, the two modes are also skewed. In such circumstances, we might need two or more components to accommodate this shape per mode in the distribution, which implies that four or more components are needed to model the distribution successfully.
It is also important to note that a mixture model is not the same as a piecewise model. The latter has also been used in mapping and splits the dependent variable in fixed ad hoc intervals and then assumes a different model distribution in each part. 49
The flexibility of mixture distributions comes at the cost of more involved estimation. The analyst needs to make judgements about (1) where to include the conditioning variables and (2) the number of components. Conditioning variables might affect the mean of each component or the probability of component membership or both. In addition, choosing the appropriate number of components involves estimating models with increasingly larger numbers of components until an acceptable model has been found. Thus, a considerable number of possible models need to be thoroughly investigated. There are practical challenges associated with fitting mixture models estimated using maximum likelihood. One of the problems relates to the presence of several local maxima in the likelihood function. Convergence to a solution does not imply that the consistent solution has been found because the optimisation algorithm could have converged to a local maximum. To identify the global maximum one can use a global optimisation algorithm such as simulated annealing. However, global optimisation algorithms are slow in comparison. Alternatively, the model can be estimated using a large number of random starting values and selecting the model with the largest likelihood. Both methods have advantages and disadvantages. A second problem arises when estimating mixture models of normal distributions with different component variances. In such circumstances, the likelihood becomes unbounded as the variance of one of the components tends to zero. As Aitkin points out, this is not a ‘real’ problem;66 it arises because the normal distribution cannot represent the likelihood when the variance tends to zero. Essentially, the component becomes a probability mass but the likelihood contribution of the density of that component becomes infinite. Provided that certain regularity conditions are met, the consistent solution will correspond to a local maximiser. 65
The first mixture model developed specifically to deal with the idiosyncrasies of PBMs was the ALDVMM. 50 The model was based on mixtures of densities similar to those underlying the tobit model but allowing for a gap between one (full health) and the next value in the PBM. It was originally developed with the characteristics of the EQ-5D-3L UK value set in mind. Here, we have generalised the ALDVMM to accommodate the boundaries of any PBMs. The model is also able to reflect the gap between full health and the next feasible health state, according to the characteristics of whichever PBM or value set is of interest, and has the additional option of not reflecting any gap at all but treating the distribution as continuous between the upper and lower bounds. All of these developments are encompassed in the freely available Stata command ALDVMM. 67
The beta mixture model
The development of the beta mixture model followed from, on the one hand, the proven advantages of the ALDVMM in modelling EQ-5D-3L and, on the other hand, the development in a different strand of the literature of models based on the beta distribution. 55 The beta distribution is very convenient when it comes to modelling PBMs; it is a bounded distribution, as are all PBMs, and can accommodate a number of different shapes: by varying its mean and precision parameter, the distribution can be symmetric or asymmetric and bell-, J-, or U-shaped. Although the beta distribution is bounded in the interval (0,1), a standard transformation can be used to change its support to any finite interval such as those covered by different PBMs. The disadvantage of the beta distribution is that the boundaries are outside its region of support. In some cases, a small amount of noise is added to the observations on the boundary to pull them inside the support region. This solution can work but only as long as the number of observations on the boundaries is relatively small. It has been shown that the beta distribution is very sensitive to large numbers of observations at the boundaries59 and the solution above might severely distort the distribution. In those cases, one can mechanically add mass points at the boundaries, but the problem then lies in the interpretation of these probability masses. In some cases it might be easy to justify the presence of a separate mass point on the boundary, but in other cases it is mere statistical convenience.
Although the beta distribution can take many shapes, bimodality is one characteristic that it cannot reproduce. It follows that augmenting the model with mixtures provides additional flexibility as well as the ability to cope with multimodality. In the area of mapping, mixtures of beta regressions have been used to model EQ-5D-3L. 47 We modify the standard mixture model to account for the gap between full health and the next feasible values as well as allowing for different approaches to model the observations on the boundaries. Details of the model are presented in full in Gray et al. 64 The model structure is presented here briefly.
It is assumed that utility for individual i, yi, is defined at full health (1) and in the interval [τ, b], with τ denoting the highest utility value below full health and τ > b. The conditional density of yi can be written as:
where x1i, x2i, x3i are vectors of covariates affecting the mean of each component, the probabilities of component membership and the probability of a boundary value, respectively. The probabilities P(yi|xi3) are defined using the following multinomial logit model:
where γk are the vectors of corresponding coefficients. The probability density function h(.) is a mixture of C-component beta distributions:
with
and the probability of latent class membership defined by a multinomial logit model with coefficients δc:
The likelihood of this particular beta mixture model is given by:
Compared with the ALDVMM, this model generates observations at full health and those below using two different processes (two-part model). The bounded nature of the data are handled naturally by a bounded distribution. These boundaries are b, the lowest value for the PBM, and τ, the highest utility value below full health, because the mass of observations at one is being handled by the other part of the model. However, values on the boundary create a problem for this distribution, which cannot handle them without further adjustment. Small numbers of observations at the boundaries (the lowest health state value and the value of the health state immediately below full health) can usually be handled by adding a small amount of noise to those observations so that they fall just inside the boundaries. However, a substantial amount of observations at the boundaries needs to be handled by adding a mass point at either or both of the boundaries to avoid distortion. Although this adaptation makes the approach appropriate for the features of the typical health utility distribution, it will increase the number of model parameters. By contrast, ad hoc mass points are not necessary when using the ALDVMM because observations can be generated at those boundary values.
Indirect methods: systems of ordinal regressions using copulas
As research and our understanding of PBMs progresses, it is inevitable that new versions of PBMs are developed. Concerns regarding the lack of sensitivity of the three-level version of the EQ-5D and the usual pile-ups of observations at full health owing to its coarse structure led to the development of a new five-level version: the EQ-5D-5L. The model introduced here was developed specifically for the purpose of testing the consistency between the responses to the EQ-5D-3L and EQ-5D-5L and to assess the likely impacts for economic evaluation of moving from the original three-level version to the newer five-level version. The NICE methods guide that was published in 201315 suggests that either version of the EQ-5D could be used in appraisal submissions once a valuation set for the EQ-5D-5L became available. However, the consequences of using different versions of the EQ-5D could not be explored until a preliminary version of the EQ-5D-5L valuation was published in 2016,68 with a final version published in 2018. 6
The standard mapping case needs to be performed in only one direction, mapping from some set of clinical or other non-PBMs to the PBM of interest. In this case, to examine the similarities and differences between the different versions of the EQ-5D, mapping needs to be bidirectional, permitting the analyst to map from the EQ-5D-3L to EQ-5D-5L and vice versa in a consistent way. This consistency cannot be achieved by estimating two separate models, one for each direction, because this ignores the relationships between the parameters in both models.
The aim is to test the hypothesis that the three-level and five-level versions of the EQ-5D instrument are mutually consistent descriptors of health states and, consequently, can be used interchangeably. The model needs to be as flexible as possible to avoid imposing unnecessary restrictions that could lead to inconsistent estimates. Several important features are introduced that build on more basic indirect mapping models described in Chapter 2, Overview of different mapping approaches, Indirect methods. First, the model needs to map from the EQ-5D-3L to EQ-5D-5L and vice versa in a consistent way. For this reason, we developed a joint model of the responses to 10 ordinal regressions (five for each dimension of each EQ-5D version). Second, we allowed the structural parts of the model to differ between the EQ-5D-3L to EQ-5D-5L so that we can test the assumption that EQ-5D-3L and EQ-5D-5L share the same underlying concept but that the five-level version involves more detailed categorisation. Third, the model captures the strong association between the same dimensions in the three-level and five-level versions using a copula representation,69 thus allowing different strengths of association across the health distribution and different patterns of association across the different dimensions of the EQ-5D. Fourth, the assumption of normality underlying the ordinal equations is generalised using two component normal mixtures (see Mixture models: background) to avoid misspecification of the distribution of the errors, which could lead to inconsistent estimates. Fifth, a random latent factor affecting all responses is introduced to reflect individual-specific effects that will manifest as dependence across all dimensions in both EQ-5D versions.
A full technical account of the model can be found in Hernández-Alava and Pudney70 and in the associated Stata command, ,71 which calculates predictions based on several estimated mapping models. The command can predict from the EQ-5D-3L to EQ-5D-5L and vice versa using either the individual-level responses or a mean utility value. The model is briefly summarised below.
The model is a system of 10 latent regressions arranged in five groups, one for each EQ-5D dimension d as follows:
where X is a matrix of covariates, β3d and β5d are column vector of coefficients and U3d and U5d are unobserved residuals, as detailed below. The observed variables Y3d and Y5d are generated by the following threshold-crossing condition:
where Qk = 3 or 5 is the number of EQ-5D levels and Γkqd are threshold parameters with Γk1d = –∞ and Γk(Qk + 1)d = +∞. The residual for individual, Ukid, is decomposed into an individual effect, Vi, which induces correlations across the responses of an individual and a specific residual, εkid, correlated within dimensions but not between:
where ψkd is a set of 10 different parameters. We make the usual assumptions that, conditional on X, Vi is independent of all εkid and all εkid are mutually independent, with the exception that within each dimension d, ε3id and ε5id can be dependent. To allow for departures from normality, Vi and all εkids are assumed to have a two-component finite mixture of normal distributions. The mixture for the errors εkid is written as follows:
where π is the mixing parameter; the location (µ1, µ2) and dispersion (σ1, σ2) parameters are constrained to satisfy the usual mean and variance normalisations, which in the case of the mixture above are:
and:
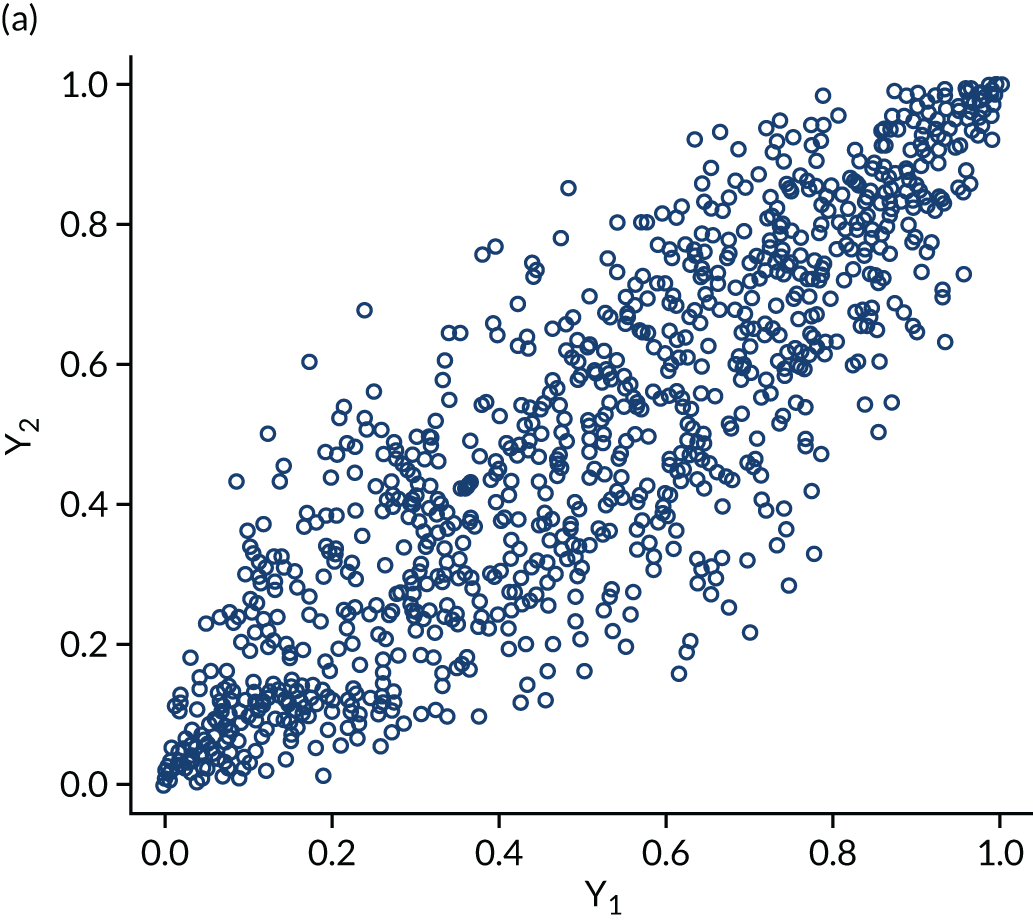
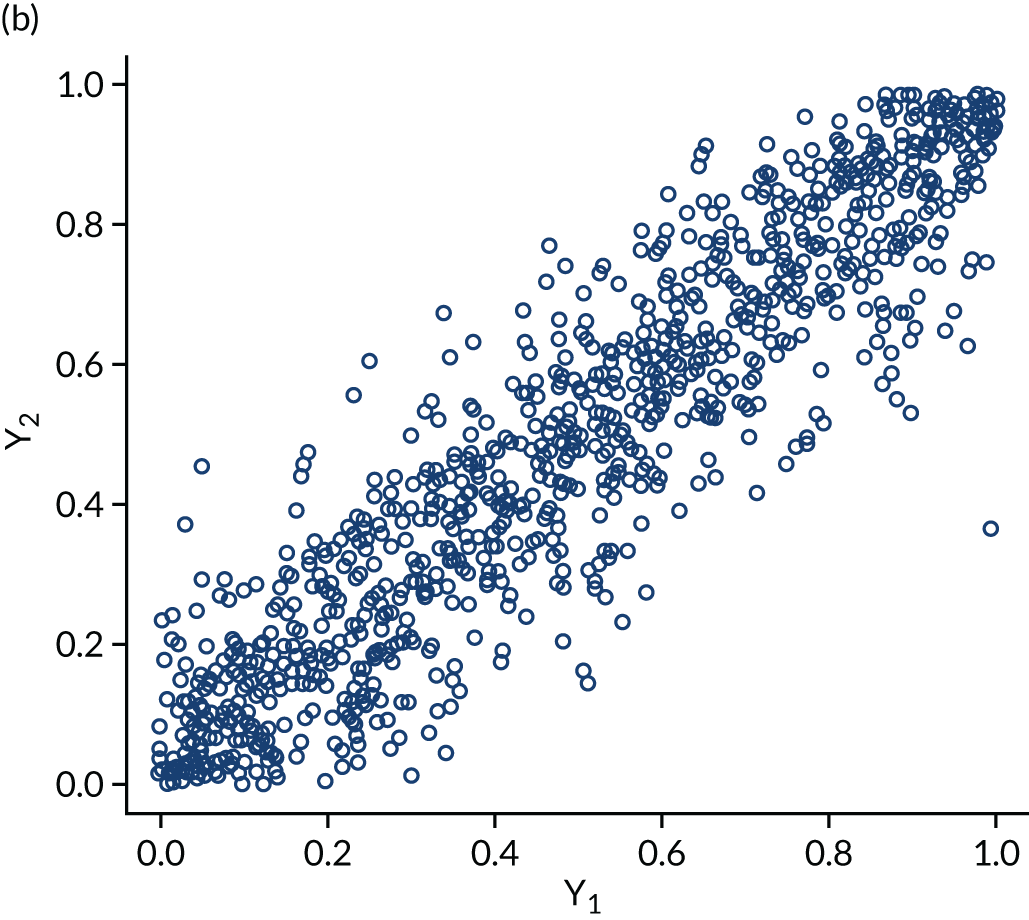
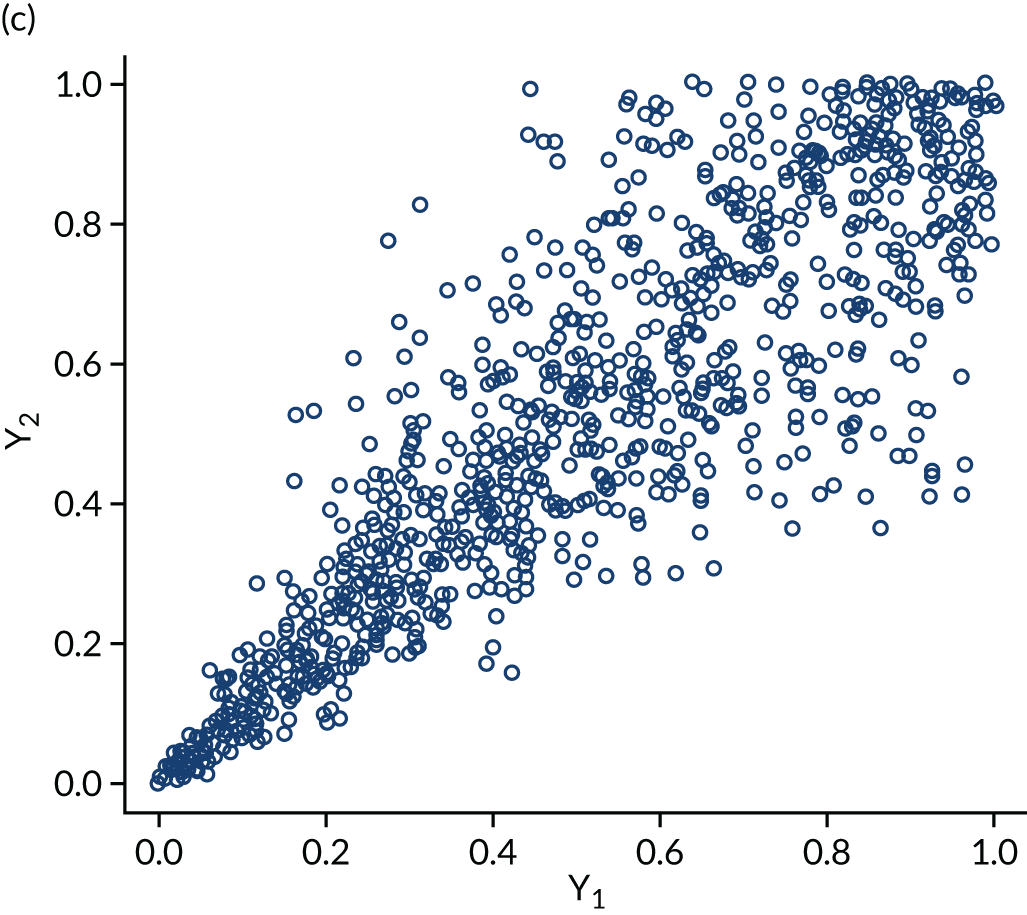
The within-domain dependency between ε3id and ε5id is captured using a copula specification66 to derive the joint distribution from the marginal distributions assumed. Copulas are very useful not only because they can be used to derive difficult joint distributions from marginals but also because they can represent a number of different dependence structures. The copulas we considered in the empirical application are independent, Clayton, Gumbel, Frank and Joe. Figure 3 shows scatterplots of samples generated by Monte Carlo simulation from three bivariate copulas, Gaussian, Frank and Clayton, all specified with a common Kendall’s τ ≈ 0.7 to illustrate the copulas’ dependence patterns. The Gaussian and the Frank copulas can exhibit positive and negative dependence, and the pattern of dependence is symmetric in both tails. However, compared with the Gaussian copula, the Frank copula exhibits weaker dependence in the tails, and dependence is strongest in the middle of the distribution. This is clearly seen in Figure 3, in which the points on the tails of the Gaussian copula are closer together than those on the tails of the Frank copula. However, in the middle of the distribution the points are closer together in the Frank copula than in the Gaussian. By contrast, the Clayton, Gumbel and Joe copulas do not allow for negative dependence, and dependence in the tails is asymmetric. The Clayton copula exhibits strong left-tail dependence (see Figure 3c, in which the points on the left-hand side are close together) and relatively weak right-tail dependence. Thus, if two variables are strongly correlated at low values but not so correlated at high values, then the Clayton copula is a good choice. The Gumbel and Joe copulas display the opposite pattern, with weak left-tail dependence and strong right-tail dependence. The right-tail dependence is stronger in the Joe copula than in the Gumbel, and thus the Joe copula is closer to the opposite of the Clayton copula.
FIGURE 3.
Scatterplots of pseudorandom samples drawn from three different bivariate copulas. (a) Gaussian copula; (b) Frank copula; and (c) Clayton copula.
An additional Stata command, ,72 developed during this project, allows analysts to estimate a simplified version of the model of the five bivariate ordinal regressions for each dimension separately. This version of the model may be used in cases where the full multivariate model is not needed; it still preserves the flexibility of the copulas for joining a pair of dimensions but does not allow for correlations across dimensions.
Predictions: mean versus distribution
Little attention has been paid to how to interpret, assess and use the results from mapping studies in economic evaluations. In particular, there has been confusion about methods for the reflection of uncertainty and variability from mapping studies.
Some authors73–77 have stated that mapping underestimates uncertainty because the sample variance of the data is always larger than the variance of the in-sample predictions. When using the expected value to predict, the sample variance of the predictions will always be smaller than the variance of the sample data because the mean predictor can only predict the variation in the utilities owing to the observed covariates. If the economic evaluation requires only the mean utility, using the mean predictor presents no problems because QALYs are a linear function of the profile of utilities over time. If, for some reason, an estimator of the variance of utilities is needed, a consistent estimator can be obtained by calculating the variance of the predictive distribution of the utilities as long as the mapping model is correctly specified; the variance of the predictions is not an appropriate estimator and should not be used. 51,70
The following sections illustrate these points using a simple case study, with data drawn from patients with RA. In brief, the data are drawn from FORWARD (the National Databank for Rheumatic Diseases)78 and have been the subject of a detailed mapping study in which the data were fully described. 51 A brief description can be found in Chapter 4, Case study data set: FORWARD. Purely for the sake of simplicity, we will consider a linear regression model that estimates health utilities using the EQ-5D-3L UK tariff as a function of the Health Assessment Questionnaire (HAQ), which is a commonly used measure of functional disability ranging from 0 (no functional disability) to 3 (maximum functional disability). In practice, there are reasons why a linear regression is unlikely to be appropriate in this situation (see Chapter 2, Overview of different mapping approaches, Direct methods), and additional covariates should be used. 50,51 Everything illustrated here applies equally to other model types, irrespective of the number of covariates and the health utility values being used as the dependent variable.
Predictions from mapping models
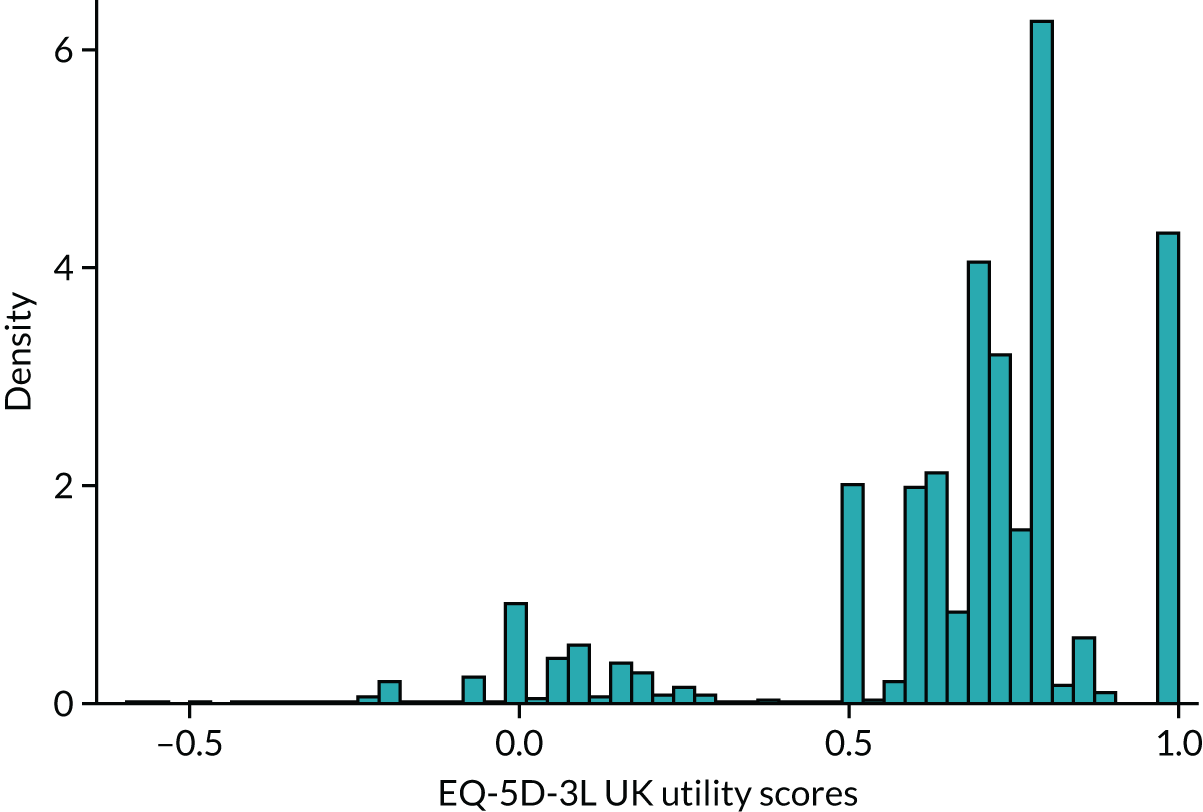
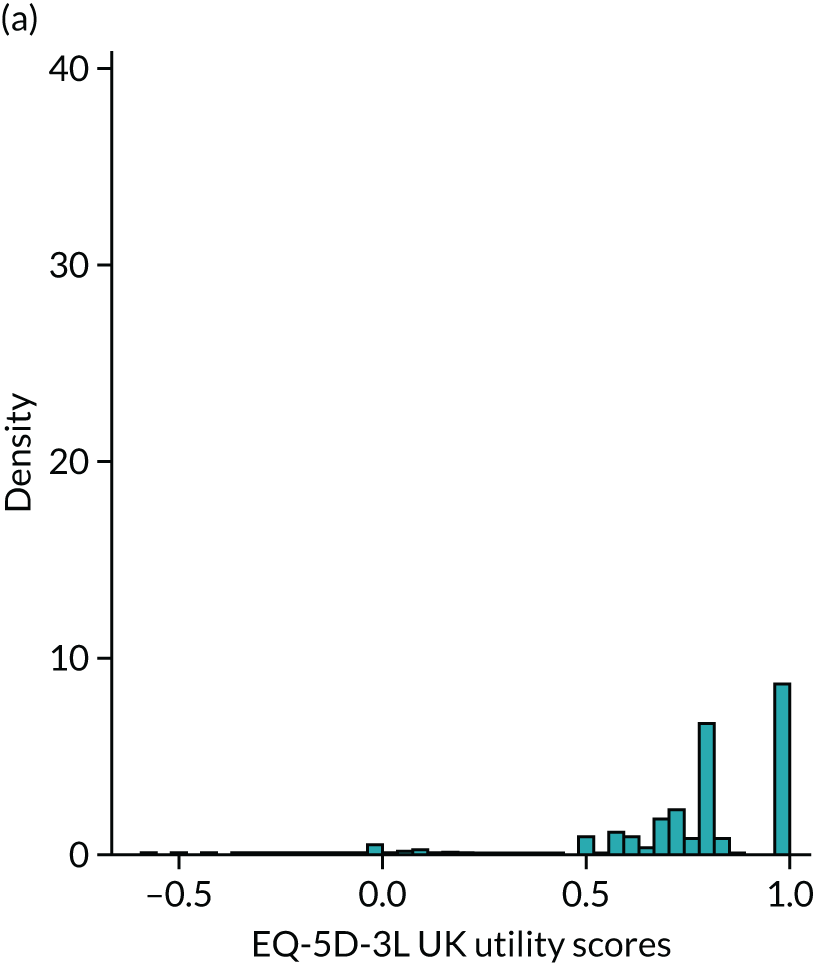
Figure 4 provides a plot of the distribution of EQ-5D-3L (UK valuation) scores from all 100,398 observations in the sample that have both EQ-5D-3L and HAQ data. It shows that the health utilities for individual patients in the sample span the whole feasible range of the EQ-5D-3L: from –0.594 (the worst heath state described by the EQ-5D-3L) to 1 (full health). The HAQ scores for these patients also vary: all the way from the least degree of functional disability (0) to the maximum (3). It is also the case that in the sample there are patients with the same level of HAQ but different levels of EQ-5D-3L.
FIGURE 4.
Distribution of EQ-5D-3L UK valuation in FORWARD (n = 100,398).
If we model the EQ-5D-3L using a simple linear regression with the HAQ as the sole explanatory variable then we are assuming that, at the population level, there is a relationship between the EQ-5D-3L and HAQ (the population regression line):
where the εi are independent and identically distributed error terms assumed (for simplicity) N(0,σ2) for individual i. This model implies that, conditional on the HAQ, the EQ-5D-3L has a normal distribution with mean:
and variance:
This means that one can never predict EQ-5D-3L values perfectly for every individual in the sample using the mean predictor because, even if α and β were known with complete certainty, for each and every value of the HAQ there is an entire distribution of values of the EQ-5D-3L in the population. In the statistical model this is reflected by the presence of the latent variable ε, which, being random itself, imparts randomness to the EQ-5D-3L. The latent variable ε exists at the population level. It does not disappear as the sample tends to the population. In other words, the model reflects the fact that individuals are different from each other. Not every person with the same HAQ value has the same EQ-5D-3L value in the data or in the population and the statistical model does not assume that they do. Indeed, individual-level data exhibit a much greater range of variation compared with aggregate-level data. This is because there are many factors unique to individuals, such as their own tastes and preferences, which cannot be observed. These factors are therefore included in ε, typically making σ2 a large component of the variation in the dependent variable. This is one of the reasons why summary measures of fit based on differences between the data and the predictions (an estimate of ε for the individual), such as R2, mean absolute error (MAE) and root mean squared error (RMSE), are quite insensitive to model specification changes (see Model comparisons).
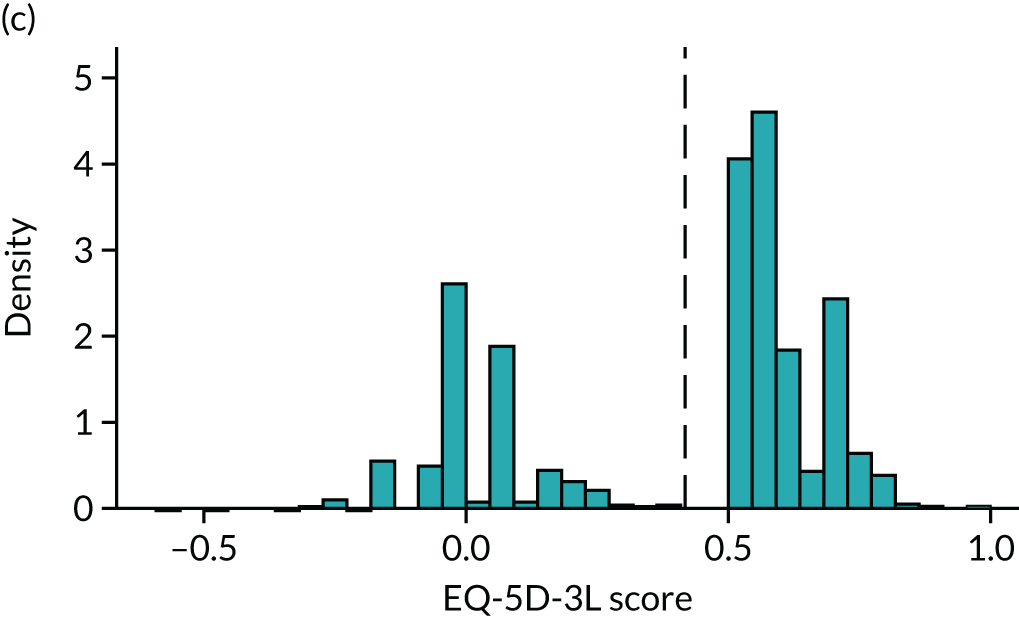
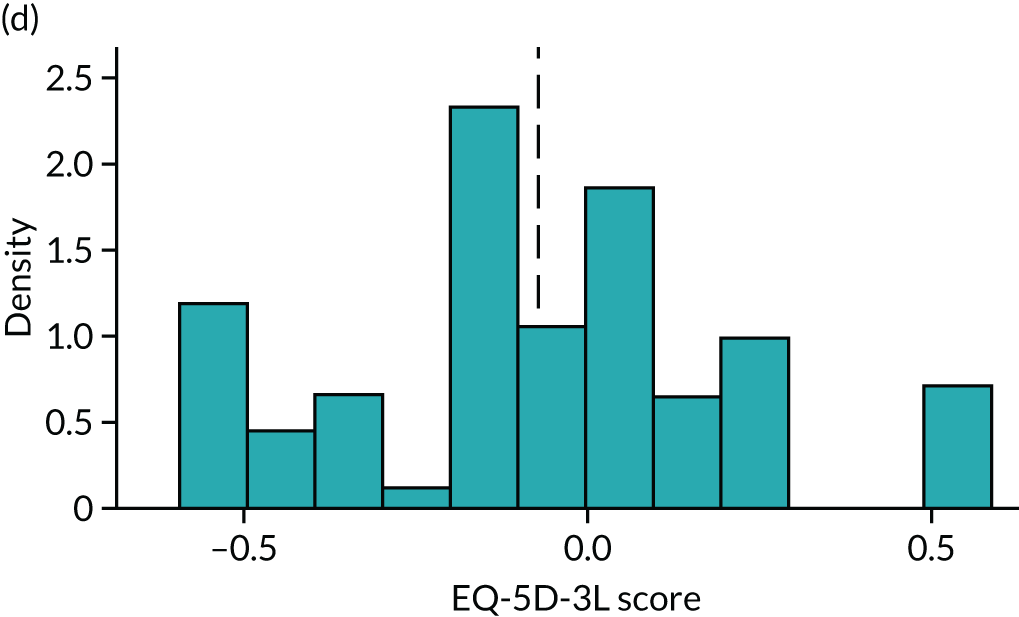
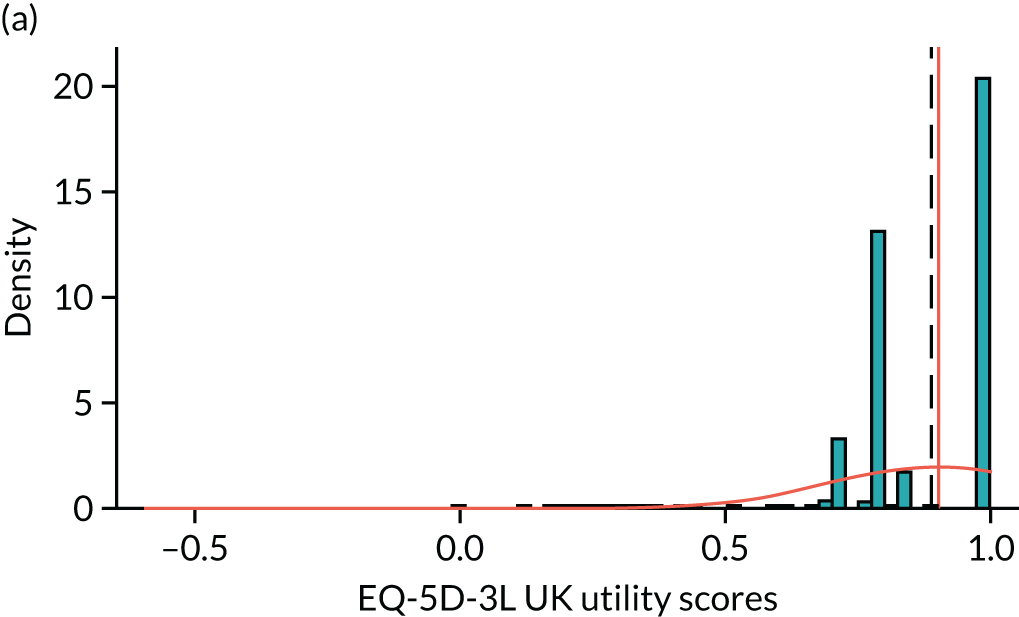
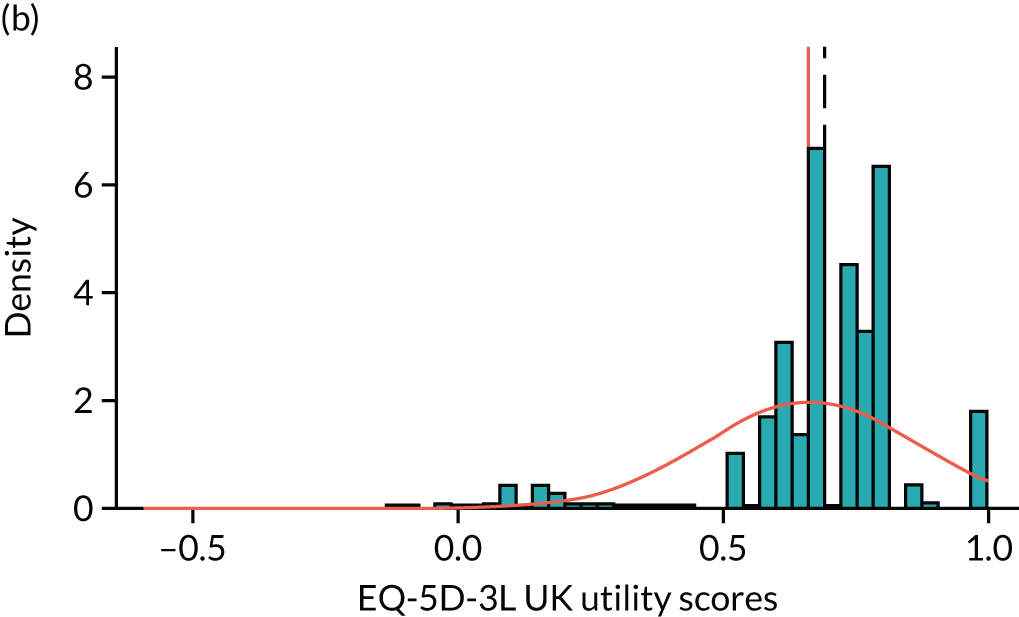
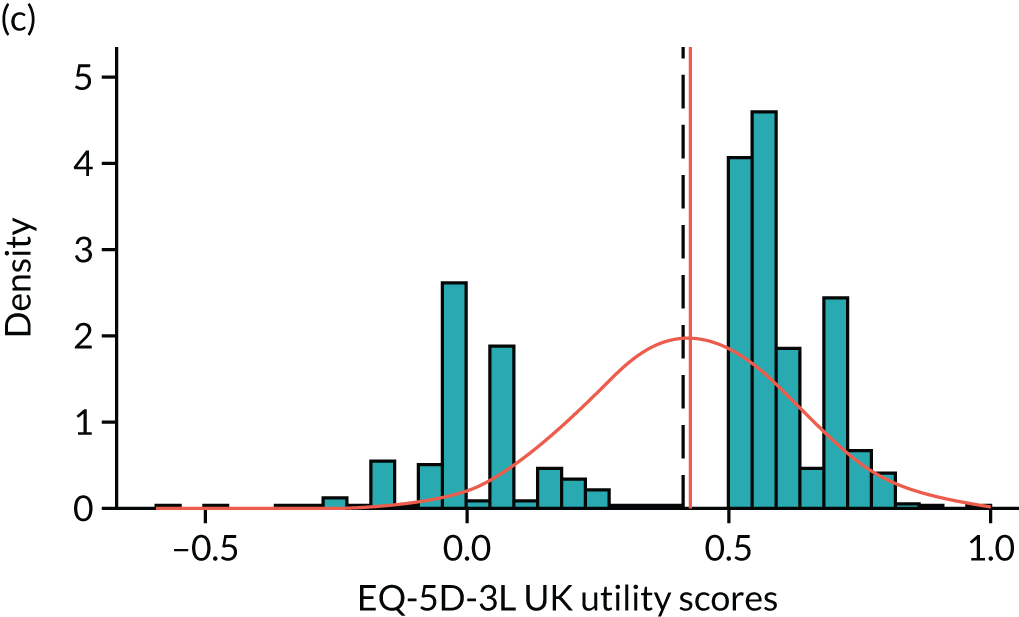
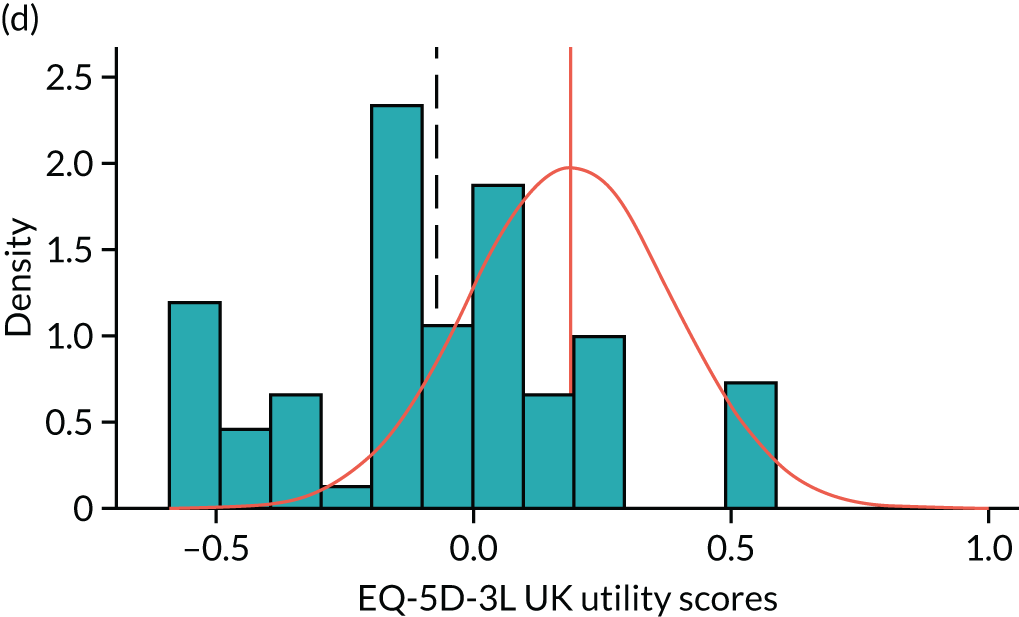
To expand on this issue: Figure 5 takes four example HAQ values (0, 1, 2 and 3) and separately plots the distribution of EQ-5D-3L health utility values for all the patients in the sample data that have these HAQ scores.
FIGURE 5.
Distribution of EQ-5D-3L scores at four different values of HAQ (FORWARD). (a) HAQ = 0; (b) HAQ = 1; (c) HAQ = 2; and (d) HAQ = 3. Vertical dashed lines indicate the mean health utility of those four sample groups (conditional distributions).
Suppose we want to use our statistical model to predict EQ-5D-3L scores conditional on HAQ scores, as might typically be the case for a cost-effectiveness model that had health states defined by these HAQ scores. If α^, β^ and σ^2 denote the estimated parameters from the linear regression above, then we can find our estimates of Equations 14 and 15 using:
and σ^2, respectively. Equation 16 is our prediction, that is, our best guess of what the mean of the conditional distribution (see Equation 14) is. These predictions must by definition be equal for every individual with the same covariate(s): they yield the expected EQ-5D-3L value conditional on HAQ value. Our prediction differs from the actual EQ-5D-3L value for any individual for two reasons. First, Equations 14 and 16 will differ because of sampling error (assuming that the functional form is right). α^ and β^ are estimated parameters associated with uncertainty because they are drawn from a finite sample of patients. The degree of that uncertainty will reduce with larger samples. Second, for each HAQ level, EQ-5D-3L differs from its mean by εi owing to variability between individuals in the population. This variability is not reduced by increasing the sample size.
To this point, it would seem reasonable that we would want a mapping model to be able to predict accurately, that is, we want the predictions from the model (the expected value conditional on covariates) to be close to the sample means for patients with the same covariates, or at least to assess the reasons why they are not close. What is not reasonable is to compare the distribution of the predicted values with the distribution of the original data. Individual patients’ utility values exhibit marked variability, even after conditioning on covariates, as illustrated in Figure 5. Predicted values from a mapping regression model simply give the average values for a set of covariates, stripping out the variability.
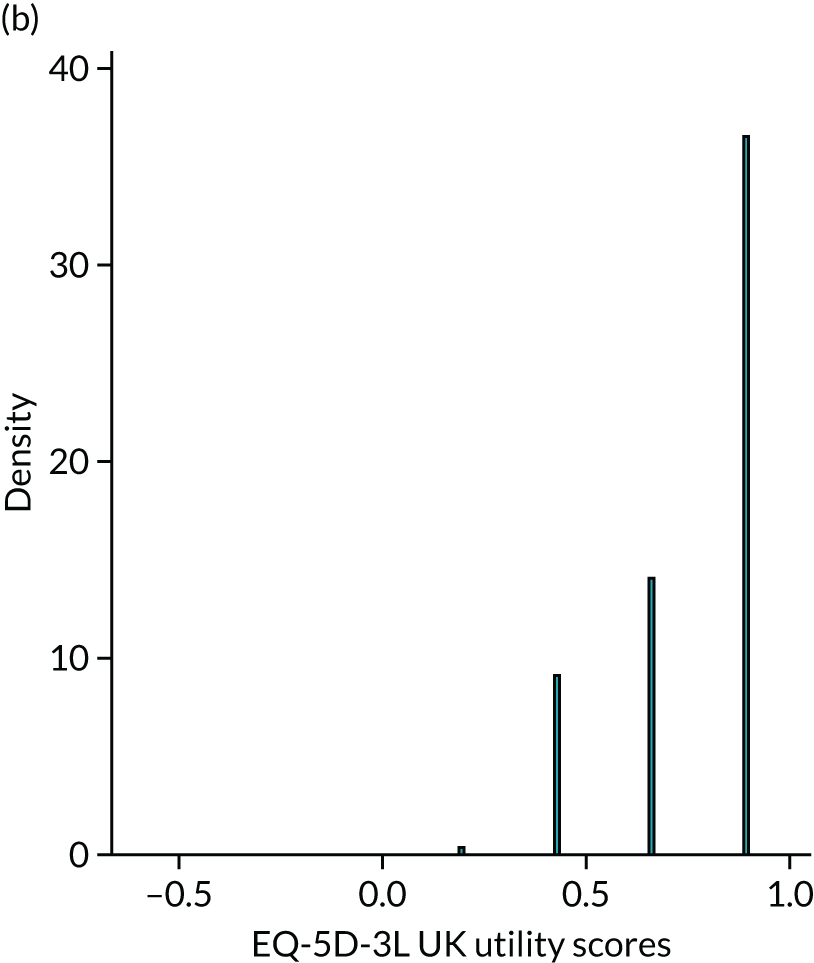
Figure 6 illustrates this for the HAQ example. Figure 6a reproduces the original data from those patients in the sample that had a HAQ of either 0, 1, 2 or 3. Figure 6b is the plot of the four predicted values conditional on HAQ. These distributions are very different, as they should be. The fitted values are conditional means, and therefore fit only four EQ-5D-3L values to each of the four HAQ values. The raw data include patient-level variability that the predictions do not. Note, for example, that no prediction yields a EQ-5D-3L value of 1 (full health) whereas in the original data there is a mass of observations at 1, typical of the EQ-5D-3L. Even for the group of patients who indicated that they have no functional disability (HAQ = 0), their mean EQ-5D-3L utility value is not 1. A utility value of 1 (full health) could be the mean for any set of patients with the same HAQ score only if every single one of them had that EQ-5D-3L value of 1.
FIGURE 6.
Comparison of (a) the sample distribution and (b) the distribution of predictions for the FORWARD data with HAQ values of 0, 1, 2 and 3.
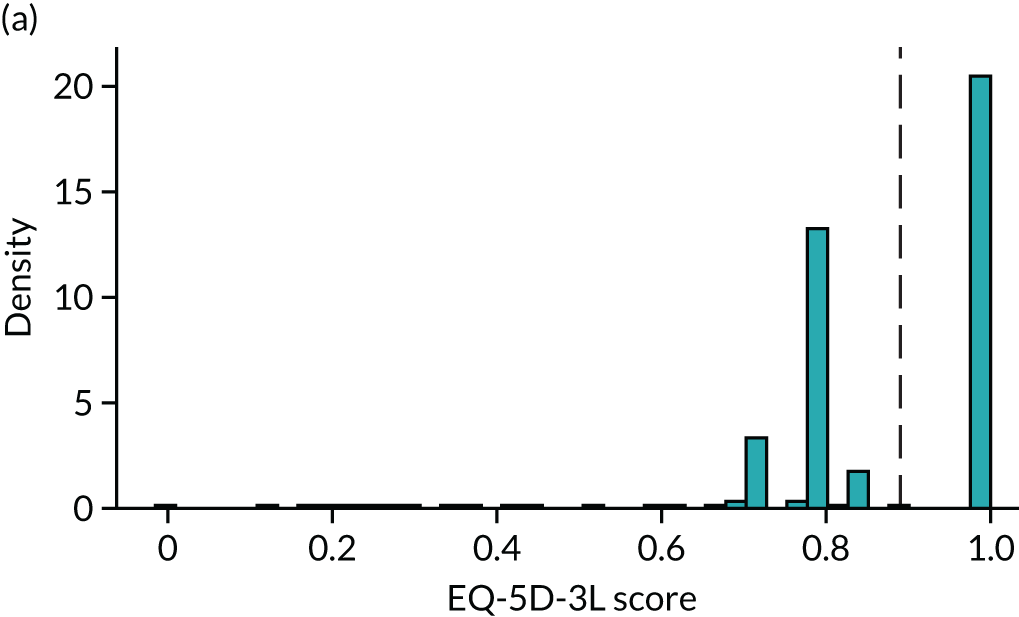
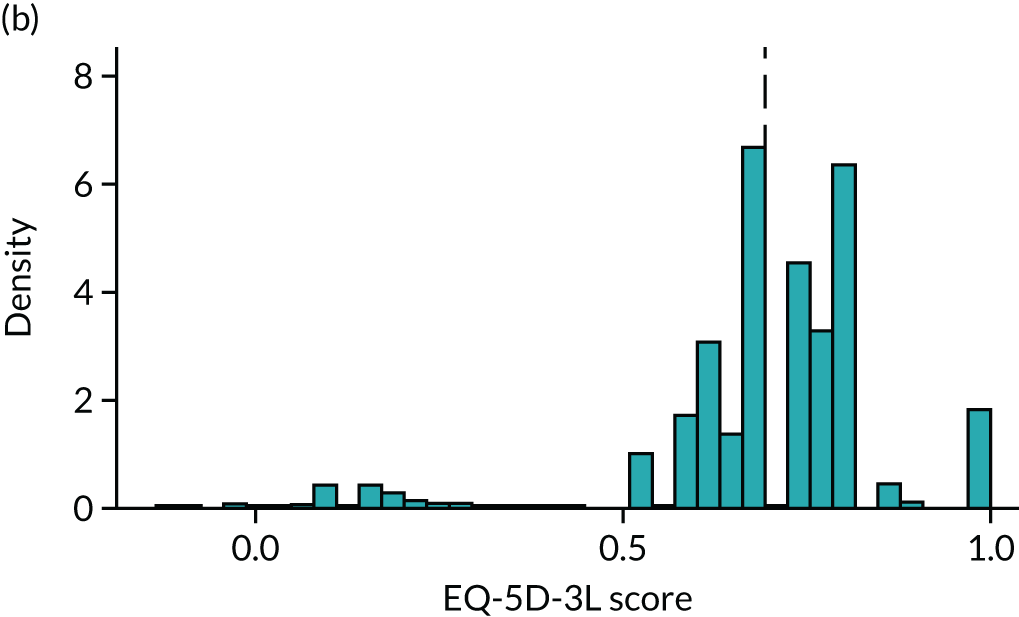
It would be valid, and indeed an important assessment of fit, to compare the predictions and the means in the data (see the vertical dashed lines in Figure 5). In this example these predictions are 0.902, 0.664, 0.426 and 0.189 for HAQ values of 0, 1, 2 and 3, respectively. The sample means for these same groups are 0.890, 0.692, 0.414 and –0.073, respectively: the point estimate of the mean EQ-5D-3L for patients with a very high HAQ (extreme functional disability) is higher than the sample average for that group by a substantial degree.
It is not valid to compare the distribution of the data to the distribution of the predictions. As discussed in Predictions: mean versus distribution, it has often been claimed that mapping underestimates uncertainty, meaning that the variance of the predictions is smaller than the variance of the sample data or that the range of the predictions is smaller than the range of the data. Figure 6 shows that not only is the shape of the distribution different between the predicted values and the sample data but the variance is indeed also substantially lower in the former, as it should be. In fact, in this case, it is approximately half that of the original data. But these two measures of ‘variance’ refer to two different concepts and are not comparable. In fact, the variance of EQ-5D-3L in the sample is made up of two components: one relates to the variability explained by the HAQ (i.e. the predictions) and the other relates to the variability of ε (i.e. σ2). Thus, the variance of the original data is always higher than the variance of the predictions.
Table 2 further illustrates this point with some examples from mappings that we have conducted. The examples cover a range of models, PBMs and sample sizes. In all cases, the difference between the variance of the sample data and the estimated variance from the model is negligible as expected. Of course, the variance from the predicted values, which does not reflect the patient level variability, is substantially lower.
| Case study | Data | Linear | Mixture | Response | |
|---|---|---|---|---|---|
| ALDVMM | Beta | ||||
| Rheumatoid arthritis: EQ-5D-3L51 | |||||
| Sample/estimated variance | 0.070 | 0.068 | 0.066 | 0.065 | |
| Variance of the predictions | 0.036 | 0.038 | 0.038 | ||
| Ankylosing spondylitis: EQ-5D-3L53 | |||||
| Sample/estimated variance | 0.098 | 0.088 | 0.097 | 0.091 | |
| Variance of the predictions | 0.043 | 0.053 | 0.055 | ||
| Heart disease: EQ-5D-5La | |||||
| Sample/estimated variance | 0.043 | 0.043 | 0.043 | ||
| Variance of the predictions | 0.026 | 0.026 | |||
| Heart disease: SF-6Da | |||||
| Sample/estimated variance | 0.018 | 0.017 | 0.018 | ||
| Variance of the predictions | 0.012 | 0.012 | |||
| Varicose veins: EQ-5D-3La | |||||
| Sample/estimated varianceb | 0.053 | 0.053 | 0.053 | ||
| Variance of the predictionsb | 0.010 | 0.009 | |||
| Sample/estimated variancec | 0.048 | 0.051 | 0.051 | ||
| Variance of the predictionsc | 0.013 | 0.012 | |||
In the case of mapping for CEA, good practice requires a reflection of the uncertainty around the predicted values. The information with which to do this is contained in the variances (and covariances) of the estimated regression coefficients, which are α and β in the linear regression HAQ example. For non-linear models such as the ALDVMM, the covariance matrix of all the estimated parameters is needed. This includes all the regression coefficients as well as all the variances of the error terms because predictions for a non-linear model depend on all the model parameters. Repeated sampling of the coefficients, drawing on the variance–covariance matrix, and using them in recalculating the predictions generates the conditional distribution of mean EQ-5D-3L. This is a standard method used to capture parameter uncertainty using probabilistic sensitivity analysis. 79
Using mapping models to simulate data
The use of predicted values from mapping, with appropriate assessment of uncertainty, is clearly important for economic evaluation. A standard cohort-based decision model would require exactly these inputs. However, in some situations the cost-effectiveness analyst’s requirements will extend further. Often there will be a need to not only estimate the mean health utility value for a health state defined by the covariates in the mapping model but also impute actual data at the patient level. This would be the case where an individual patient level simulation model is being used. Indeed, often this type of model is used precisely because of the need to reflect patient variability to obtain an unbiased estimate of cost-effectiveness. 80 Alternatively, where a CEA is being undertaken alongside a clinical trial that has not collected health utility information, mapping is used to impute missing data for each patient and, as for all types of missing data, the analyst may not wish to simply impute the conditional mean value.
We described in Predictions: mean versus distribution, Predictions from mapping models, how the error term, ε, for the linear regression allows the statistical model to reflect variability at the individual level. The distribution of EQ-5D-3L conditional on HAQ will be normally distributed with mean equal to the prediction (α^+β^HAQi) and variance σ^2. So we can simulate data from the regression outputs using these assumptions about the error term to reflect the estimated degree of variability.
Figure 7 shows these predicted conditional distributions for our example HAQ values of 0, 1, 2 and 3 and superimposes them on the corresponding conditional distributions from the original data (as in Figure 5). For our linear regression model we can see that the mean from the simulated values is close to the sample means for each HAQ group, except those with a HAQ value of 3. The shape of that distribution does not match very closely to the original data and it is not constrained to the feasible range of the EQ-5D-3L. These features are important for assessing the credibility and suitability for potential uses of a mapping model in subsequent cost-effectiveness analyses. Reporting of results in this way has helped to demonstrate the performance of other model types previously. 50,51,62
FIGURE 7.
Distributions of EQ-5D-3L by HAQ group: sample vs model. (a) HAQ = 0; (b) HAQ = 1; (c) HAQ = 2; and (d) HAQ = 3. The dashed line represents the sample mean; the red line represents the mean prediction based on the model.
Model comparisons
The primary purpose of mapping models is to serve as an input to cost-effectiveness analyses. Therefore, any model comparisons need to take into account the possible ways in which a mapping model could be used in this context.
By far the most widely used criteria to select the appropriate model in the existing mapping literature have been measures of goodness of fit of the model such as R2/R¯2, and measures of predictive accuracy such as mean error (ME), MAE and RMSE. There are several problems when using these measures as model selection criteria in mapping. Mapping models are estimated using individual-level data and, typically, relatively few covariates of potential relevance are available in the mapping data set and/or have any realistic prospect of being used in the CEA. At the individual level there is substantial variation and factors which are typically unobserved might determine the response variables. These unobserved factors are often relatively large and, consequently, the data tend to be quite noisy, affecting measures of goodness of fit (R2/R¯2), which will tend to be relatively low compared with studies using more aggregated data (see Predictions: mean versus distribution). Furthermore, the scale of the dependent variable, health state utility, is small. Using the UK/England valuation sets, the length of the range intervals for the EQ-5D-3L, EQ-5D-5L, SF-6D and HUI3 is 1.594, 1.285, 0.699 and 1.359, respectively (see Table 1). The small range of values coupled with the relatively large contribution of unobserved factors results in relatively insensitive measures of predictive accuracy (MAE and RMSE). Often, differences between alternative mapping models will be detected only at the third or fourth decimal place of these measures. Without recognising the constrained scale of health utility, it may be tempting to conclude that model differences are slight and unimportant. However, even small differences can have serious consequences for the CEA because the incremental benefit of an intervention appears in the denominator of the ICER. Incremental benefits are typically quite small, so the ICER is very sensitive to very small differences between mapping functions. Furthermore, MAE and RMSE are aggregate measures that might conceal systematic patterns in the predictions. Systematic biases in the conditional means of the models may be a sign of model misspecification.
Some studies report the ME. Where this is close to zero, as will be the case for a linear regression estimated using OLS, this is used as support for the credibility of the mapping model despite the concerns about its suitability raised in Chapter 2, Overview of different mapping approaches, Direct methods. It is important to note that estimators such as OLS, which minimise the residual sum of squares, essentially ensure that, as long as there is a constant term in the linear regression, the mean of the predictions equals the mean of the dependent variable in the sample. Thus, the ME will be effectively zero with slight departures owing to the numerical precision used in the calculation. In fact, one could estimate a linear regression model without any covariates and find that just the inclusion of a constant will yield a ME of approximately zero. This illustrates how this criterion for model selection is not fit for the purpose of selecting a mapping model.
More recently, information criteria such as the Akaike information criterion (AIC) and the Bayesian information criterion (BIC) have also been used. One complication of these information criteria, which also applies to measures of goodness of fit such as such as R2/R¯2, is that not all models that can be used for mapping can be compared on this basis because models must have the same dependent variable. In particular, direct and indirect approaches model different dependent variables and therefore their AIC and BIC cannot be compared directly. Models based on the beta distribution need rescaling of the dependent variable to the range of the health state value set, invalidating comparisons of AIC and BIC even with other models that use direct approaches.
Another important issue is that often these criteria select different models. MAE and RMSE are based on different scoring functions that are computed at the individual level and then averaged to give a summary measure of predictive accuracy. MAE and RMSE are similar in that all individual error measures are positive, unlike ME, in which positive and negative errors can cancel each other out. RMSE gives a higher weight to large errors owing to the squared terms and thus is sensitive to large outliers. Some researchers prefer MAE whereas other researchers prefer RMSE because large errors are seen as undesirable. In our case, this is not straightforward. Because mapping feeds into a cost-effectiveness model, what is important will depend on the specific cost-effectiveness application. If the feature that matters most for the specific CEA is not having any large errors, RMSE might be more useful. However, in other cases MAE might be more appropriate to select the model. Therefore, without knowledge of the specific CEA and the consequences of large versus small errors in utility estimation, it is not possible to be prescriptive about which measure of predictive accuracy is better in various scenarios. It is important, however, that as much information as possible is provided in an accessible way so that the economic analysts using the results of the mapping can make a judgement about its suitability for each specific application.
Both AIC and BIC may also lead to different models being selected. Both models are based on penalised likelihoods but the penalty imposed for model complexity by BIC is higher than that for AIC; thus, BIC will tend to choose models with less parameters than AIC. This issue always arises when estimating mixture models with different numbers of components. Both AIC and BIC first decrease and later increase with the number of components as the increasing number of parameters starts to outweigh the benefits in terms of increased likelihood. The inflexion point tends to occur at a lower number of components for BIC than for AIC owing to its higher penalty.
Hernández Alava et al. 50 and, more recently, Fuller et al. 54 have proposed some graphical methods suited to the specific case of mapping to help with model selection as well as also providing vital information for the economic analysts to select the right mapping model for their analysis and/or design suitable for sensitivity analyses. These graphs have been shown to be of significant value when deciding on the best mapping model in many applications (see Chapter 4 for several examples).
For many cost-effectiveness analyses it is only necessary that the mapping model is capable of predicting the conditional means correctly without systematic biases that could affect the results of the cost-effectiveness model. In other cases, patient-level simulation is required and the mapping model needs to be able to reproduce the full conditional distribution of health utilities (see Predictions: mean versus distribution). The graphical methods described in this section are based on attempting to identify problems with the conditional means and the full conditional distribution, which could be a sign of model misspecification.
The usual procedure of comparing the distribution of the predictions with the distribution of the data is not appropriate and seemingly arises from confusion regarding what the term 'prediction' stands for (see Predictions: mean versus distribution). The methods proposed here are based on (1) comparisons of the predictions (conditional means) with means of the data grouped according to at least one of the conditioning variables and (2) comparisons of the distribution of the data with the distribution of the data that would be generated by the estimated model. These two points are important for model selection because they highlight features that are important for a mapping model and directly relevant to the economic analysts using the results of the mapping. These graphs reveal the presence (or absence) of systematic problems in the conditional means (predictions) as well as problems with the assumed underlying distribution that can cause both distortion of the conditional means and the full conditional distribution.
To illustrate the value of these graphs, a random sample of 3000 individuals from FORWARD (see Chapter 4, Case study data set: FORWARD, for details of the survey) is used to estimate three different models, mapping from the HAQ and pain to the EQ-5D-3L. The example mapping models are chosen to demonstrate the usefulness of the graphs in identifying problems with the mapping models and their use in practice (see Chapter 4 for practical applications in which these graphical methods are used with a variety of mapping models). The three chosen models are (1) a linear regression, because this is one of the most commonly used mapping models, (2) a two-part beta regression, because of its ability to appropriately take into account the bounded nature of health utility data and the mass of observations often present at full health (a restricted version of the beta mixture model in The beta mixture model, with only one component), and (3) a three-component ALDVMM, which can, in addition, deal with shapes not easily accommodated by a single distribution and the relatively large gap between full health and the next feasible value. The beta mixture model (see The beta mixture model) could be used in place of the ALDVMM without altering the conclusions; however, it has the added complication of requiring a decision about whether or not to add mass points at the lowest utility value and the first value below full health. To abstract from those complications, we used the ALDVMM instead. All models use age, gender, HAQ and pain as conditioning variables.
Table 3 presents the usual measures of predictive accuracy and selection criteria for the three estimated models. As expected, the ME of the linear regression is essentially zero by construction. The linear regression shows the worst MAE and RMSE, but notice the small differences across the three models. Owing to the rescaling of the dependent variable needed when using the two-part beta regression, the only two models for which the information criteria can be compared are the linear regression and the ALDVMM. Both AIC and BIC point towards selecting the three-component ALDVMM.
| Measure | Linear regression | Two-part beta regression | Three-component ALDVMM |
|---|---|---|---|
| ME | –3.94e-17 | 0.01001 | –0.00004 |
| MAE | 0.12896 | 0.12469 | 0.11861 |
| RMSE | 0.17084 | 0.16764 | 0.16495 |
| AIC | –2078.389 | –3636.775a | –3460.150 |
| BIC | –2048.357 | –3570.705a | –3315.997 |
It may be tempting to select the linear regression owing to its simplicity and the small differences in MAE and RMSE. Plots of the predicted means versus data group means and distribution of the data versus the distribution derived from the estimated model are very useful to aid understanding of differences between models and the potential impact of those differences when translated into economic evaluation. Figure 8 presents these plots for the three models. Figures 8a–c present the graphs of the average group predictions versus the data means by intervals of HAQ. The linear regression and the two-part beta regression have problems capturing the conditional means of the EQ-5D-3L, especially at low values of EQ-5D-3L, where they systematically overpredict. If a health technology were to increase the levels of HAQ from those low values, both mapping models would tend to underestimate the benefit of the health technology. The two-part beta regression would tend to do so to a lesser extent than the linear regression. It is also worth noting that, in this case, at the highest levels of HAQ (extreme functional disability), the linear regression tends to overestimate slightly the mean EQ-5D-3L, whereas the two-part beta regression captures that mean better. This is expected because the two-part beta regression (estimated using the Stata command ,64 which allows for the gap) is designed to accommodate the large mass of observations at full health and the gap and does this very well. The three-component ALDVMM captures the conditional means fairly well across the different HAQ levels and does not exhibit any systematic patterns that could be cause for concern. Figures 8d–f plot the cumulative percentage of EQ-5D-3L data versus the cumulative percentage implied by the estimated models. Looking at these plots gives us an understanding of the reasons behind the problems with the conditional means. There are several problems with the linear regression. Although EQ-5D-3L data are bounded, there is nothing in the linear regression model that restricts the distribution (and, therefore, its conditional mean) within the boundaries of EQ-5D-3L; this may induce distortion in the distribution of the conditional means because in bounded distributions the mean and the variance are related. Another problem is the presence of a large peak at full health. Continuous distributions defined in the real space have very thin tails and find it difficult to generate a mass of points at the end of the tail even after conditioning on the variables available for mapping. As a result of these two issues, the estimated linear model generates points well above the full health value of 1. In this case, the predictions (the means of the conditional distributions) are all below the threshold value of 1, but it is not uncommon for even the conditional means to go above 1 when predicting either within the sample or, even more commonly, out of sample when using the models in a CEA. The two-part beta regression is specifically designed to deal with the mass of observations at full health and the gap and fits that part of the distribution very well. What neither of these two models can do is replicate the bimodality of the data, and their generated distribution completely misses those observations at EQ-5D-3L levels < 0.5. Once enough flexibility is introduced, in this case through the use of mixtures via the ALDVMM, the systematic overprediction of the conditional means at low levels of HAQ disappears and the model seems to capture the conditional means much better overall, not just at the bottom end. At the same time, the distribution implied by the estimated model is much better aligned with the distribution of the data. Even if interest for a particular application lies only in predicting the conditional means, model misspecification may distort those conditional means, as shown in this example, and those problems cannot be appreciated by looking at only the standard measures of prediction accuracy.
FIGURE 8.
Plots of mean prediction vs. data group mean and cumulative percentage of actual data vs. model. (a) Linear regression: means over HAQ DI groups; (b) two-part beta regression: means over HAQ DI groups; (c) three-component ALDVMM: means over HAQ DI groups; (d) linear regression model; (e) two-part beta regression model; and (f) three-component ALDVMM model. DI, disability index.
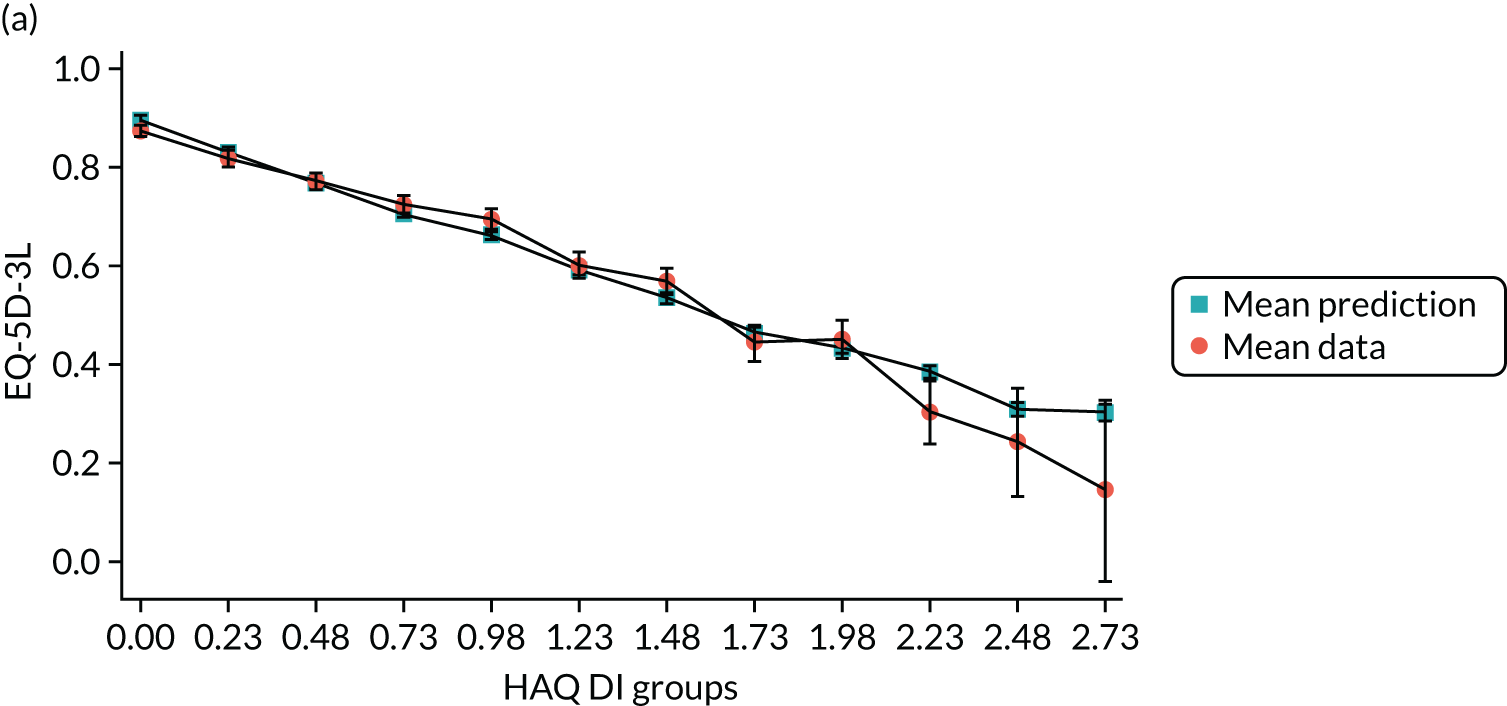
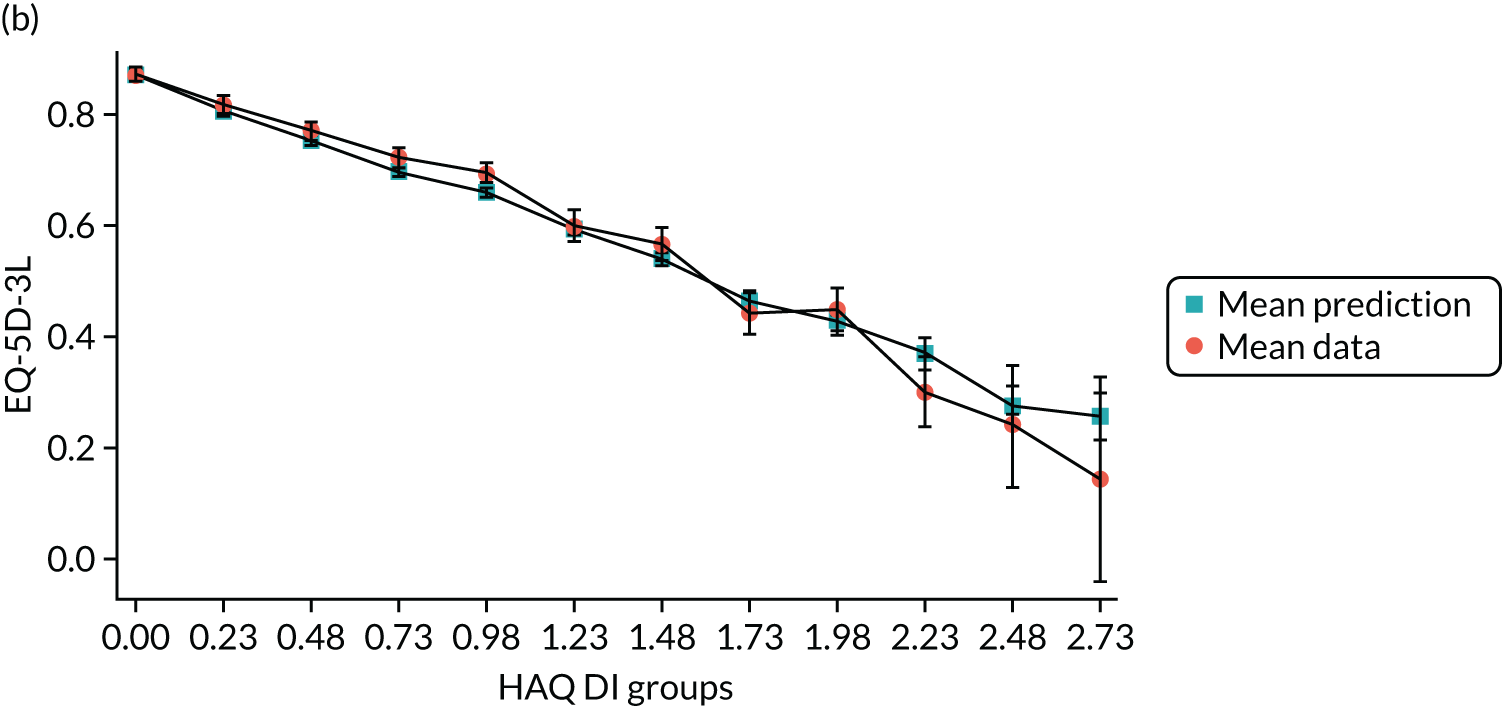
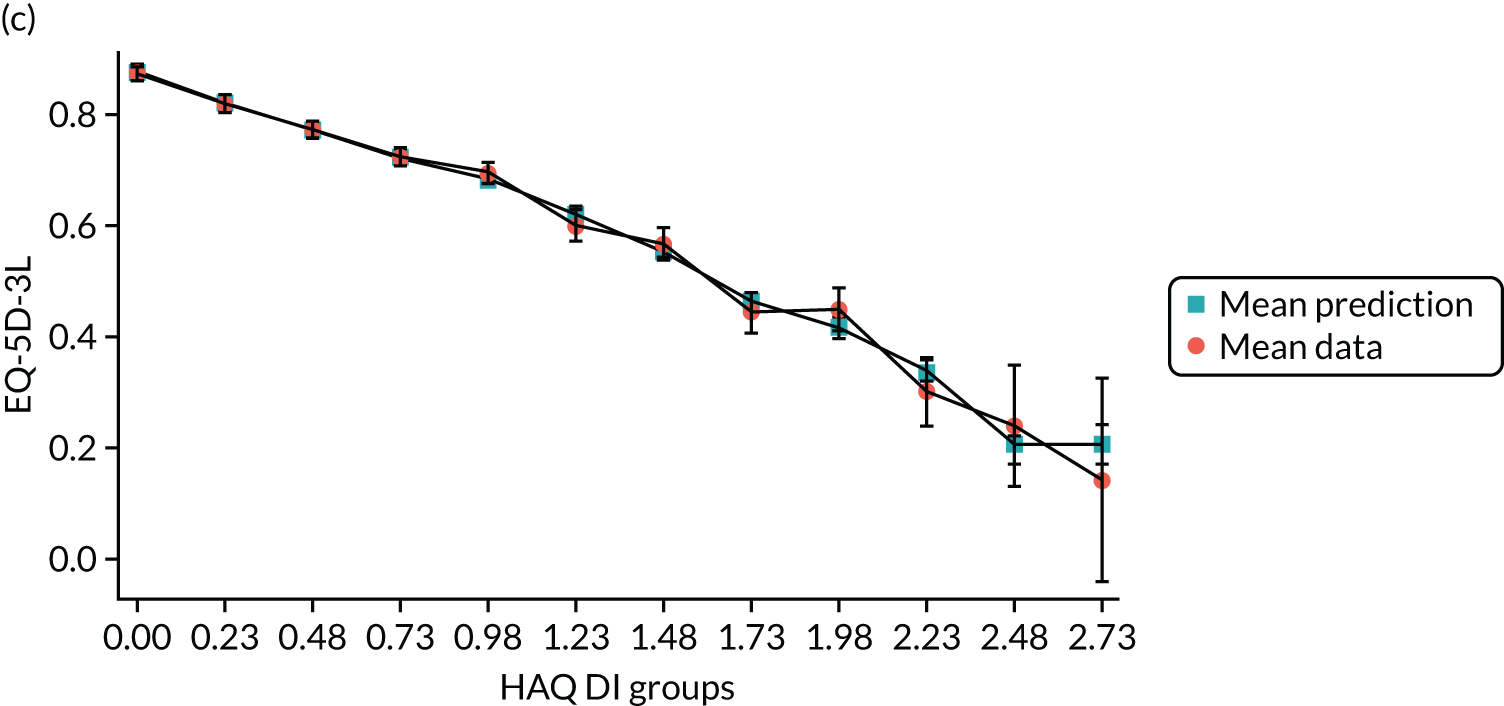
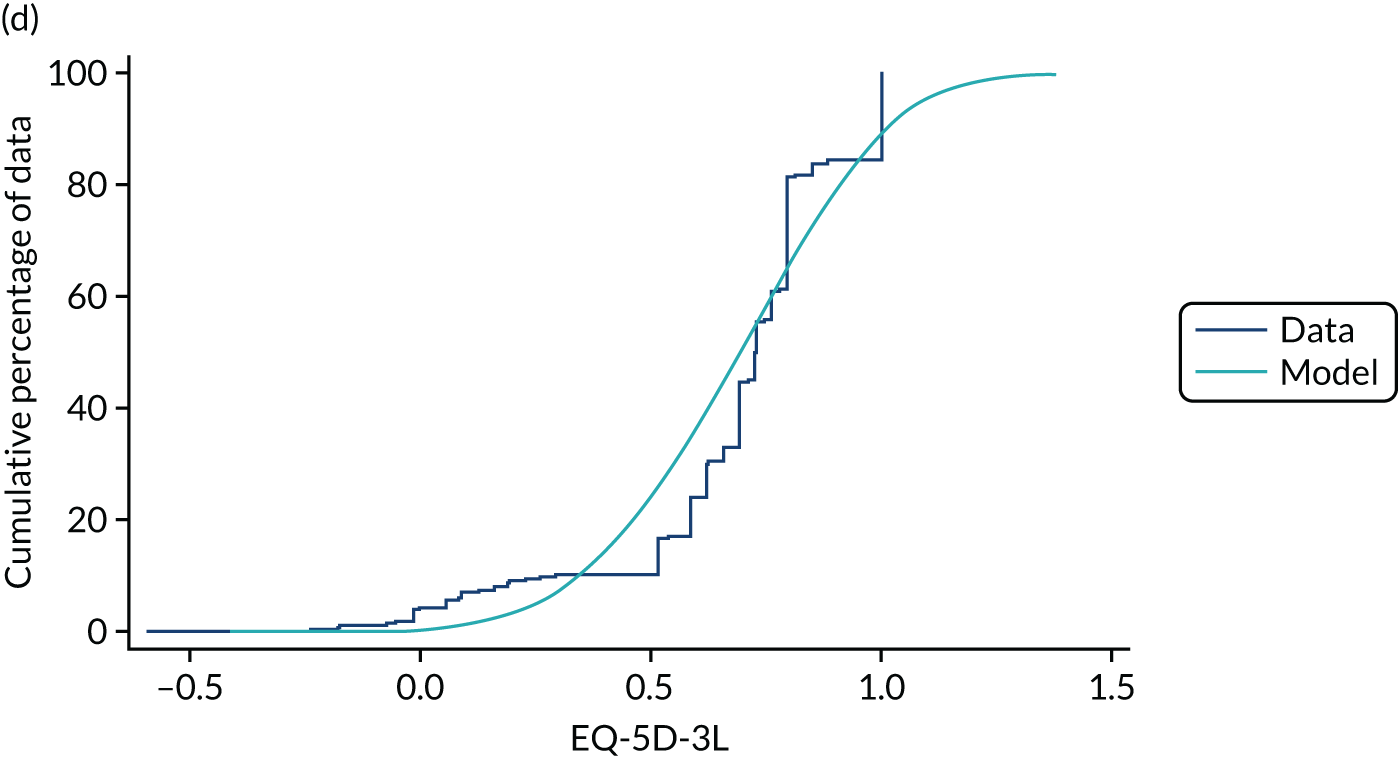
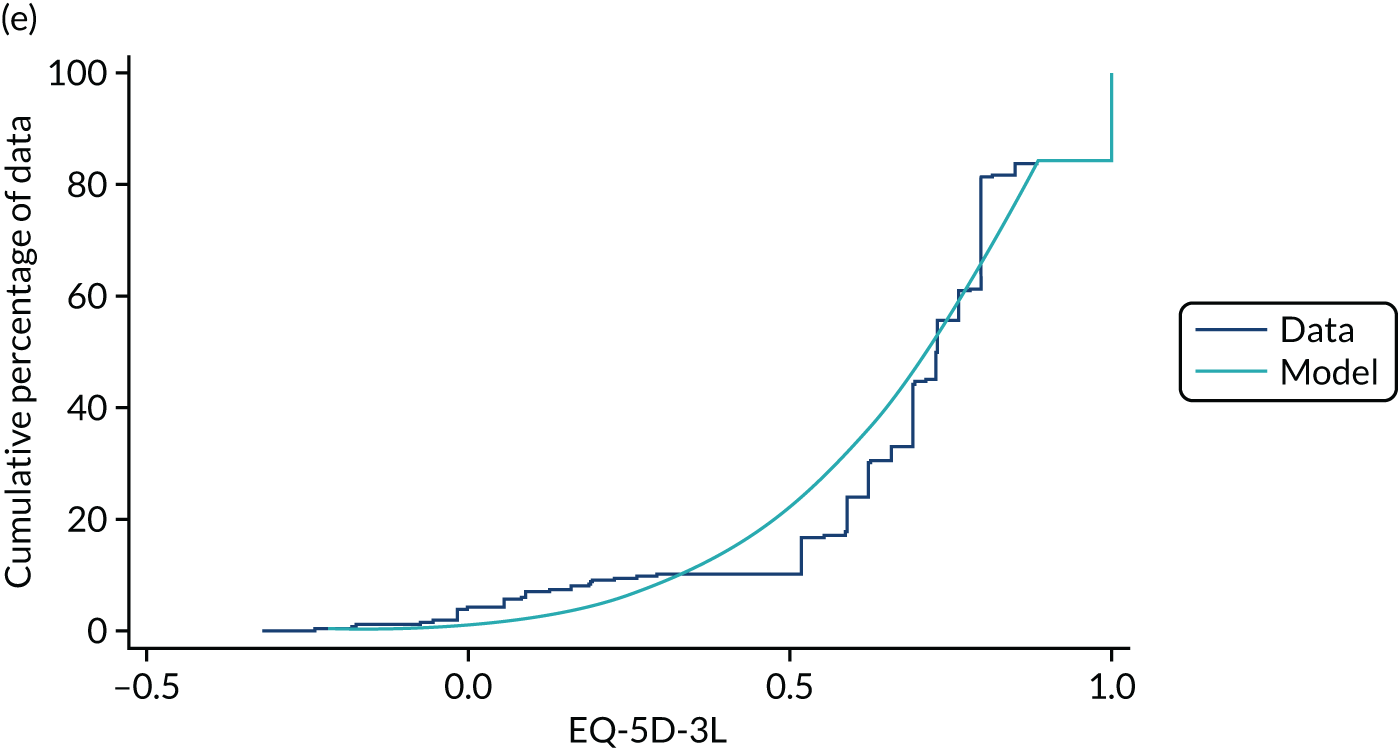
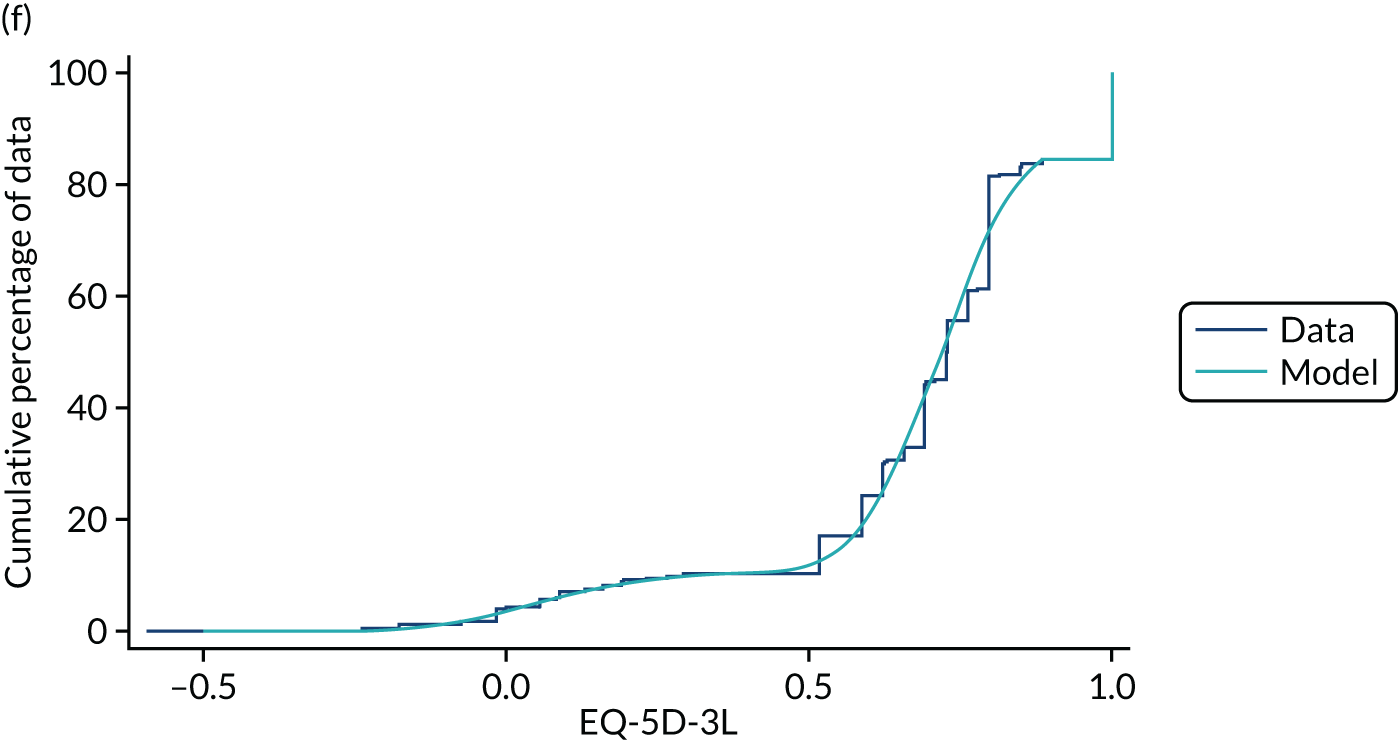
These plots also illustrate the theoretical issues highlighted in Chapter 2, Direct methods, and show, on the one hand, the consequences of using a linear regression to model PBMs data in terms of underpredictions/overpredictions of the conditional means and misspecification of the distribution and, on the other hand, how allowing for the features of health utility data overcomes those problems. The two-part beta regression is able to accommodate most of the health utility data features, so in principle it is a good candidate; however, even a flexible distribution such as the beta distribution cannot quite accommodate the features of the data. This is the reason why a finite-mixture version of the two-part beta regression was developed during this project.
These plots are also very useful for analysts using the mapping models as a resource because they clearly show the areas where the conditional means might not be accurate and where the full conditional distribution is not fitting well. The information in the plots will guide the analysts in their decision about selecting a mapping model if more than one is available and in identifying additional sensitivity analyses that need to be carried out to assess the robustness of the results.
Validation of any statistical model should begin by looking at whether or not the model captures the main features of the data within the sample. If there are obvious problems within the sample, such as those described above for the linear model, these are only going to get worse when predicting out of sample.
Chapter 4 Case studies
This chapter presents a summary of the case studies used in this project. We include models that are able to address all features of health utility data. We also include linear regressions in some of the comparisons, given their popularity. Unidirectional case study comparisons concentrates on the typical use of mapping from a disease-specific measure to a PBM. The findings from the case study comparisons also apply to any model with a PBM measure as the target outcome measure, regardless of the variables used to map from. Multidirectional mapping case study presents the findings for a case study in which the aim was to get a single consistent model to map in two directions.
Unidirectional case study comparisons
We tested and compared the performance of different mapping methods in seven applied case studies providing 15 data sets for comparison purposes. These case studies were selected to provide a broad cross-section of disease areas, target PBMs and covariate types. Further details on these data sets and how they may be accessed are available from the authors on request.
Case study data sets
Glasgow Outcome Scale
Data from the Victorian State Trauma Registry (VSTR) were used. The VSTR is a population-based database that has collected information on all major trauma cases in the state of Victoria, Australia, since 2001. 81 Patients are included if they meet any of the following criteria: injury severity score of > 12; admission to critical care for more than 24 hours, with mechanical ventilation for at least part of that time, as a result of injury; urgent surgery secondary to major trauma; or death due to injury. The study population comprised consecutive adults (aged ≥ 16 years) enrolled in VSTR with significant traumatic brain injury (TBI) (head-region abbreviated injury scale severity score of ≥ 3) and injured between January 2008 and June 2013. The VSTR contains an extensive data set of demographic, physiological, injury, investigation, and treatment and outcome variables. The study sample size was 3437.
Outcome in TBI effectiveness studies is conventionally assessed using the basic or extended Glasgow Outcome Scale (GOS), measuring death and severity of disability using an ordinal scale. The basic scale has five points, as shown in Table 4.
| Score | Scale level | Description |
|---|---|---|
| 1 | Death | Severe injury or death without recovery of consciousness |
| 2 | Persistent vegetative state | Severe damage with prolonged state of unresponsiveness and a lack of higher mental functions |
| 3 | Severe disability | Severe injury with permanent need for help with daily living |
| 4 | Moderate disability | No need for assistance in everyday life; employment is possible but may require special equipment |
| 5 | Low disability | Light damage with minor neurological and psychological deficits |
The extended scale expands levels 3, 4 and 5 of the basic scale, resulting in an eight-category scale (Table 5).
| Score | Scale level |
|---|---|
| 1 | Death |
| 2 | Vegetative state |
| 3 | Lower severe disability |
| 4 | Upper severe disability |
| 5 | Lower moderate disability |
| 6 | Upper moderate disability |
| 7 | Lower good recovery |
| 8 | Upper good recovery |
Mappings to the EQ-5D-3L from both the basic and extended scales were performed. Full details of the study are reported in Ward Fuller et al. 54
Functional Assessment of Cancer Therapy-Breast
Data from three Phase III clinical studies of patients with locally recurrent or metastatic breast cancer that measured both the EQ-5D-3L and Functional Assessment of Cancer Therapy-Breast (FACT-B)82 were pooled for this analysis. The three trials were as follows:
-
The Treatment Across multiple liNes wIth Avastin (TANIA) trial,83 which comprised 494 human epidermal growth factor receptor 2 (HER2)-negative locally recurrent/metastatic breast cancer patients whose disease had progressed on or after first-line bevacizumab combined with chemotherapy. They were randomised to receive standard second-line chemotherapy either alone or in combination with bevacizumab.
-
The MARIANNE study, which randomised 1095 patients with HER2-positive advanced breast cancer to one of three treatment arms: control (trastuzumab plus taxane), trastuzumab emtansine plus placebo or trastuzumab emtansine plus placebo plus pertuzumab.
-
The Batman study, which was an open-label, single-arm, multicentre UK study of the safety and tolerability of bevacizumab when combined with taxane monotherapy as first-line therapy of 50 patients with triple-negative metastatic breast cancer.
The FACT-B is a self-reported instrument that measures health-related quality of life of breast cancer patients. 82 It comprises five subscales: physical well-being, social well-being, emotional well-being, functional well-being and a breast-cancer-specific subscale. The subscales have seven items, with the exception of emotional well-being, which has six items, and the breast-cancer-specific subscale, which has nine. Items are rated from zero to four, with zero and four representing ‘not at all’ and ‘very much’, respectively, and a total score is derived. Items can be positive or negative, for example ‘I have lack of energy’ or ‘I feel close to my friends’. Higher scores for negatively worded items correspond to better health. The total FACT-B score ranges from zero to 123, and is calculated by adding the scores from each of these subscales after accounting for negative or positive wording. Lower scores indicate better health in this scoring.
Full details are reported in Gray et al. 84
Sydney Asthma Quality Of Life Questionnaire
We used data from the Multi-Instrument Comparison (MIC) project data set, which collected data from respondents in six countries: Australia, Canada, Germany, Norway, the UK and the USA. 85 In total, 8817 individuals completed 12 instruments relating to their health or well-being. Data were collected from a representative healthy cohort and from patients in eight clinical areas. The study was designed to allow comparisons between health and well-being instruments. Patients who self-reported specific health conditions were asked to complete disease-specific outcome measures as well as numerous other generic outcome measures for well-being and health utility. In total, 856 respondents self-reported asthma and completed the Sydney Asthma Quality of Life Questionnaire (AQLQ-S). Data were available for respondents’ age and sex as well as their EQ-5D-5L and HUI3 values. After removing observations with missing values in any of the required variables, the final sample for analysis was 852.
Gray et al. 37 report as follows:
The AQLQ-S was designed as a measure of quality of life for adult patients with asthma. The questionnaire contains 20 questions within four domains (symptoms, activity limitation, emotional function and environmental stimuli). Each of the questions allows a response on a 0–4 scale, with zero representing no problems at all. The scores for each question are averaged to produce an overall AQLQ-S score between zero and four. Although there are many different versions of the AQLQ, the AQLQ-S is recommended by the European Medicines Agency (EMA)86 and has been validated. 87
MacNew Heart Disease Health-related Quality of Life questionnaire
We again used data from the MIC study. 85 The MIC data set contains variables on demographic variables, health and well-being, disease-specific health measures and health state utility measures. Disease-specific questionnaires were given to patients who self-reported the relevant diseases. In total, 943 respondents self-reported having heart disease and completed the MacNew Heart Disease Health-related Quality of Life (MacNew) questionnaire. Data were available on respondents’ age and sex as well as their EQ-5D-5L and SF-6D values in all cases, leaving a final sample of 943 observations.
The MacNew questionnaire was developed to measure quality of life in heart disease patients. The questionnaire contains 27 questions and generates an instrument that aims to quantify the effects of heart disease and treatment of heart disease on physical and emotional health as well as social function. Each of the questions allows a response on a scale of one to seven, with one representing the most severe problems and seven representing no problems at all. The scores for each question are averaged to produce an overall MacNew score between one and seven.
European Organisation for Research and Treatment of Cancer quality of life questionnaire
We used data from the Trastuzumab emtansine versus treatment of physician’s choice for pretreated HER2-positive advanced breast cancer (TH3RESA) study. TH3RESA was an open-label, phase-III trial that randomised patients from 14 September 2011 to 19 November 2012. A total of 602 patients recruited from medical centres in 22 countries across Europe, North America, South America and Asia-Pacific took part. Eligible adult patients had HER2-positive, unresectable, locally advanced or recurrent breast cancer or metastatic breast cancer and had received two or more HER2-directed regimens in the advanced setting, including trastuzumab and lapatinib, and previous taxane therapy in any setting, and were randomly assigned (in a 2 : 1 ratio) to trastuzumab emtansine (3.6 mg/kg intravenously every 21 days) or physician’s choice. 88 Patients with non-measurable or measurable disease according to Response Evaluation Criteria in Solid Tumors (RECIST) version 1.1 were enrolled. Patients completed the European Organisation for Research and Treatment of Cancer (EORTC) Quality of Life Questionnaire-Core 30 (QLQ-C30)89 version 3c90 at the same time as they completed the EQ-5D-3L questionnaire, from day one of each treatment cycle until study treatment discontinuation or investigator-assessed disease progression. The trial included the EQ-5D-3L and we use the UK value sets. 5 The data contains multiple observations from each individual. We report robust standard errors to reflect this.
The EORTC QLQ-C30 is an integrated system for assessing the health-related quality of life of cancer patients participating in international clinical trials. The QLQ-C30 comprises 30 questions and is a commonly used outcome in clinical trials as well as in other non-trial clinical studies. At the time of writing, the instrument had been used in > 3000 studies. 91 The QLQ-C30 is composed of both multi-item scales and single-item measures, which include a global health status/quality-of-life scale, five functional scales (physical, role, emotional, cognitive and social function), three symptom scales (fatigue, nausea and vomiting, and pain), and six single items (dyspnoea, insomnia, appetite, constipation, diarrhoea and financial difficulties). All are expressed on a scale of 0–100, with higher scores representing higher levels of functioning, higher quality of life or higher levels of symptoms.
Oxford Knee Score
We use data from the 2009–14 PROMs data set with information on > 170,000 patients. These data hold information on a number of disease-specific PROMs and PBMs. The data includes patients suffering from knee problems and contains their Oxford Knee Score (OKS) score, as well as their EQ-5D-3L measure, both before and 6 months after knee replacement surgery. The data also contain information on sex and age group (40–49, 50–59, 60–69, 70–79, 80–89 and 90–120 years of age).
The OKS was developed in 199892 shortly after the Oxford Hip Score. 93 Both are questionnaires that record patient-reported outcomes. The OKS was developed to be used in randomised controlled trials to record patient outcomes before and after surgery to help assess the success of surgery without the bias of surgeon-reported outcomes. The OKS concentrates heavily on instruments related specifically to the knee to prevent comorbidities from biasing results. Questions focus on pain, mobility and self-care. (See Dawson et al. 92 for a more detailed description of the questionnaire and its development.) It consists of 12 questions scored between zero and four, resulting in a total score between zero and 48, with 48 being the best possible response and zero representing the most severe response to every question.
Aberdeen Varicose Vein Questionnaire
We used data from the PROMs data set from 2009 to 2014, which holds information on > 170,000 patients. These data contain information on a wide range of outcome measures, both disease-specific and preference-based general health measures. The data includes patients suffering from varicose veins and records their Aberdeen Varicose Vein Severity (AVVS) score as well as their EQ-5D-3L measure; PROMs also provides information for the patients before and 3 months after they have surgery. We performed separate analyses on the pre- and post-surgery data. Data are available for 25,266 patients with valid AVVS scores in at least one time period, before or after surgery. The data also contain information on sex and age group (40–49, 50–59, 60–69, 70–79, 80–89 and 90–120 years of age). After observations with missing values have been removed, there are 13,337 and 8610 patients with information in all required fields, before and after surgery, respectively.
The AVVS score was developed in 1993 to produce a reliable outcome measure for patients suffering from varicose veins. 94 The questionnaire, developed by Garratt et al. ,94 includes a range of questions referring to the patient’s experiences relating to their varicose veins during the most recent 2 weeks, including questions on pain, use of medication, swelling, itching and rash. Answers to these questions are then added together and used to create a score between 0 and 100, where 0 is no symptoms and 100 corresponds to the most severe answer to each of the questions. The AVVS has been validated in previous studies. 95
Table 6 provides an overview of the key characteristics of the mapping case studies. We did not consider the same model types in all case studies. These studies were used to develop the evidence base, with each study conducted sequentially and selecting or developing model types for testing based on the findings of previous studies.
| Disease area | n | Target PBM | Primary covariates | Methods |
|---|---|---|---|---|
| Brain injury | 3437 | EQ-5D-3L | GOS | ALDVMM |
| Breast cancer | 11,958 | EQ-5D-3L | FACT-B (summary score and individual items) | ALDVMM, response mapping |
| Asthma | 856 | EQ-5D-5L, HUI3 | AQLQ-S | Beta mixture, ALDVMM, linear regressiona |
| Heart disease | 943 | EQ-5D-5L, SF-6D | MacNew questionnaire | Beta mixture, ALDVMM, response mapping |
| Breast cancer | 3765 | EQ-5D-3L | EORTC QLQ-C30 | ALDVMM, linear regression, response mapping |
| Knee surgery | 136,327 | EQ-5D-3L | OKS | Beta mixture, ALDVMM, response mapping |
| Varicose veins | 13,337 pre surgery; 8610 post surgery | EQ-5D-3L | Aberdeen Varicose Vein Questionnaire | Beta mixture, ALDVMM |
Results
Results are summarised in Table 7.
| Study | PBM | Optimal number of classes, n (n tested) | Covariates for class probabilities | Model comparisons ranking | ||||
|---|---|---|---|---|---|---|---|---|
| ALDVMM | Beta mix | Disease severity | Age | 1 | 2 | 3 | ||
| GOS basic, simple model | EQ-5D-3L | 3 (4) | Yes | Yes | ALDVMM | |||
| GOS basic, detailed model | EQ-5D-3L | 3 (4) | Yes | Yes | ALDVMM | |||
| GOS extended, basic model | EQ-5D-3L | 4 (4) | Yes | Yes | ALDVMM | |||
| GOS extended, detailed model | EQ-5D-3L | 4 (4) | Yes | Yes | ALDVMM | |||
| FACT-B, summary score | EQ-5D-3L | 3 (4) | Yes | Yes | ALDVMM | Response mapping | ||
| FACT-B components | EQ-5D-3L | 3 (4) | Yes | Yes | ALDVMM | Response mapping | ||
| AQLQ-S | EQ-5D-5L | 3 (4) | 3 (4) | Yes | Yes | Beta mixture | ALDVMM | Linear model |
| AQLQ-S | HUI3 | 4 (4) | 4 (4) | Yes | Yes | Beta mixture | ALDVMM | Linear model |
| MacNew | EQ-5D-5L | 3 (4) | 3 (4) | Yes | Yes | ALDVMM | Beta mixture | |
| MacNew | SF-6D | 4 (5) | 4 (5) | Yes | Yes | ALDVMM | Beta mixture | |
| EORTC QLQ-c30 | EQ-5D-3L | 4 (5) | Yes | No | ALDVMM | Linear model | Response mapping | |
| OKS (pre operation) | EQ-5D-3L | 4 (4) | 3 (4) | ALDVMM | Beta mixture | |||
| OKS (post operation) | EQ-5D-3L | 3 (4) | 3 (4) | ALDVMM | Beta mixture | |||
| AVVS (pre operation) | EQ-5D-3L | 3 (3) | 3 (3) | Yes | Yes | ALDVMM | Beta mixture | |
| AVVS (post operation) | EQ-5D-3L | 4 (4) | 4 (4) | Yes | Yes | ALDVMM | Beta mixture | |
Glasgow Outcome Scale
The GOS study compared different specifications of the ALDVMM in terms of the number of latent classes and the covariates. The first set of models presented used a small number of covariates: basic GOS category and age. These appeared both as explanatory variables within each component and also explained the probability of component membership. From these models, the three-class model was selected as the optimal model because the addition of a fourth class improved model fit only marginally and at the expense of increased model complexity. The three-class model had lower BIC but other fit statistics favoured the four-class model.
The more detailed model showed a similar pattern in the results. Additional covariates were included in these models: sex, comorbidity and extra-cranial injury. The three-class model was again the preferred version. This version had the lowest AIC, MAE and RMSE.
In both cases, there was evidence of very good fit across the EQ-5D-3L severity range. This was true for within-sample fit and in an out-of-sample comparison of scores provided by patients 24 months post injury. There was a small degree of underprediction of EQ-5D-3L for those in good health.
Using the extended GOS as the explanatory variable in both the basic (including only age) and detailed model (additional covariates of gender, comorbidity and extra-cranial injury) yielded similar results. However, in both cases the four-class models were deemed optimal. These performed best in terms of AIC, MAE and RMSE inter alia. Within-sample and out-of-sample prediction of EQ-5D-3L at 12 and 24 months post injury also showed excellent agreement between observed and predicted values. However, there was again minor underprediction of EQ-5D-3L at 6 months for those patients with little or no functional disability.
Functional Assessment of Cancer Therapy-Breast
The FACT-B study compared ALDVMM and response mapping models. ALDVMM models beyond four classes had problems with convergence and could not be estimated. The response mapping models were estimated using seemingly unrelated regression ordered probits. Only FACT B and age were used as explanatory variables. There were only very small numbers of males in the data set.
For the models that used the FACT-B total score, the preferred model was the three-class ALDVMM. Although the four-class model had lower AIC and BIC, other measures of fit favoured the three-class variant, including the assessment of fit over the range of disease severity measured by FACT-B. The three-class model demonstrated close fit to the data at all levels except the most severe disease, where data were scant. The difference between the observed and predicted values at this level of disease severity was within 95% CIs. Simulated data from both the three- and four-class models fit the observed data very closely. Performance of the ALDVMM models was substantially better than response mapping. This applies to both the measures of summary fit and assessment of model performance at different parts of the distribution. The response mapping was particularly poor at the severe disease level.
Using the subscales for FACT-B as covariates improved model performance for all types, as expected. Again, the three-class ADLVMM was preferred, although performance of the four-class model had lower MAE and RMSE. Interestingly, although the performance of the response mapping approach improved, in many aspects this still did not yield a model that performed as well as the ALDVMM models based on total FACT-B score. In particular, the ALDVMM performed better than the response mapping approach in the middle section of the disease severity distribution.
Sydney Asthma Quality of Life Questionnaire
The AQLQ-S study37 compared a number of variants of the ALDVMM and beta mixture models predicting both EQ-5D-5L and HUI3. Because much of the testing of models had previously focused on the three-level EQ-5D, these model variants allowed us to see whether different features of the models were still required when modelling utility instruments that did not have such pronounced features as the EQ-5D-3L. For example, both instruments have a gap between full health and the next feasible health state (these next feasible health states are 0.951 in the EQ-5D-5L and 0.97258 in the HUI3). The gap created by the ‘truncation point’ in the HUI3 is substantially smaller than that in the EQ-5D-3L and, therefore, may not be a requirement for inclusion in models. We tested both types of mixture models with and without the inclusion of this truncation point and with and without the inclusion of a probability mass at this truncation point (beta mixture models).
Response mapping could not be conducted because the data lacked observations in each of the response categories of the EQ-5D-5L and HUI3 instruments. Linear regression was also used to provide further comparisons with this method. We included the AQLQ-S summary score, age, age squared and sex as covariates in all parts of the models. We also ran models that included the individual dimension scores of the AQLQ-S rather than the total score but found that results were not significantly improved.
When modelling the EQ-5D-5L, it was found that models that included the gap between full health and the next feasible value outperformed those that did not. Beta mixture models required the formal addition of a probability mass at full health to perform sufficiently well. This is an in-built feature of the ALDVMM, which does not require any adaptation to achieve this. Models without a probability mass at the truncation point did not perform better than those that omitted it. For these reasons, the optimal beta-based model has three components and a probability mass at full health but not at the truncation point. The optimal ALDVMM also had three classes. The four-component model offers improvements in RMSE, MAE and ME but has a higher BIC. Model fit over different disease severities was very similar between the three- and four-class models.
For the HUI3 model, we found that beta mixture models had to formally model the gap in utility values and incorporate a probability mass at full health. The best-performing model also included a probability mass at the truncation point and had four components, although the three-component model had a lower BIC. The ALDVMM’s performance varied by the number of components but also the inclusion of different covariates. We found that model fit was improved by the inclusion of age in the model probabilities.
Linear models performed worse for both explanatory variables in almost all relevant areas of model selection.
MacNew Heart Disease Health-related Quality of Life questionnaire
Models were compared using both EQ-5D-5L and SF-6D score as the dependent variables.
In the case of the EQ-5D-5L, for the ALDVMM the performance of three- and four-class models was very similar. The BIC favoured the three-class model and, although MAE and RMSE were superior for the four-class variant, there was very similar graphical fit. Therefore, we preferred the three-class model. Beta mixture models used the same set of covariates, including MacNew score and age, in the component probabilities. Because there were only 10 observations at the truncation point, the best-fitting beta mixture model included a mass point only at full health. Beta models produced marginally improved summary fit statistics compared with the ALDVMM models with the same numbers of components. However, it needs to be recognised that a three-component beta mixture model has more parameters in general than a three-component ALDVMM (31 vs. 26, respectively). Based on parsimony, we recommend the ALDVMM three-class model.
In the case of the SF-6D, we tested ALDVMM models up to five classes but found that the four-class model was preferred. This offered some improvement in fit over the three-class model. The specification of the beta mixture models was determined in part by the distribution of SF-6D utility values in this sample. There were only three observations at full health and, therefore, models with a probability mass at this point were not feasible. Similarly, there was only one observation at the lower limit and small numbers at the truncation point. Therefore, the beta mixture models did not include mass points at any of these three options. The ALDVMM models performed slightly better than the beta mixtures with equivalent numbers of components. The beta models also exhibited poor fit for those in the most severe MacNew-defined health states. This issue was absent from the ALDVMM models.
European Organisation for Research and Treatment of Cancer Quality of Life Questionnaire-Core 30
The ALDVMM models with up to five components were estimated, using the component scores of QLQ-C30 as explanatory variables. We found that the likelihoods for the five-component models were unreliable owing to very small variances. The optimal model has four components and included both disease-specific variables and age within the components. Only the global health status component of the QLQ-C30 was included in the class probabilities.
This model was preferred over both linear regression and response mapping (implemented using generalised ordered probit models).
Oxford Knee Score
Separate analyses were conducted of pre- and post-surgery data.
Response mapping using seemingly unrelated ordered probit models had clear problems fitting the data. The model focuses on fitting the parts of the distribution for which there are a larger number of observations at the expense of other parts of the distribution; in the pre-operation sample, predictions are poor at both the upper and the lower end of the distribution, whereas the post-operation sample is predicted relatively well at the upper end of the distribution but even more poorly at the lower end. However, this was not reflected in the summary fit statistics, which were equal to the direct, mixture-model-based approaches.
We found that the ALDVMMs, which included a gap between full health and the next feasible health state, consistently outperformed the equivalent model, which does not allow for this gap. The four-component model was the preferred variant. This was based on both the AIC and the BIC and also on the plot of the conditional distribution, which showed improved fit at the lower end of the distribution (EQ-5D-3L value < 0.25).
Like the ALDVMMs, the beta mixture models were consistently better fitting when a gap was included in the model between full health and the next feasible health state. The best-fitting models were those that included probability masses at full health, at the next feasible heath state and at the worst possible health state. The addition of a fourth component made very little difference to the model; thus, we recommend the use of the three-component model.
There was little to distinguish between the performance of the ALDVMM and beta mixture models for equivalent numbers of components when compared using plots of mean EQ-5D-3L by mean OKS or the cumulative distribution plots. The beta mixtures entail more parameters than the ALDVMM and are more arbitrarily adjusted to suit the data. Therefore, the ALDVMM model is marginally preferable.
The results for the post-operative data were very similar. Here, the poorer performance of the response mapping approach was also evident in the summary fit statistics. The ALDVMM three-component variant was preferred to the four-class model. The summary fit measures are very similar between the ALDVMM and beta mixture models and are therefore not conclusive in selecting a preferred model. The plots of the predictions also revealed no significant differences. The four-component model adds a component at around 0.6, in contrast with the three-component model, allowing a subtle improvement in model fit around this area of the EQ-5D-3L distribution. However, this improvement in fit is minor and does not warrant the addition of the extra component.
Beta mixture models that include a gap performed better than those that do not in the post-operative sample, both in terms of summary fit and from visual inspection of the predicted values and the cumulative distribution plot. We also found that the better-fitting models are those that do not include probability masses at the point adjacent to full health or the worst possible health state.
Aberdeen Varicose Vein Questionnaire
The AVVS score was used as the dependent variable in two types of mixture model analyses: ALDVMM and beta-based mixture models.
For the pre-operation data, we found that the beta-based mixture models performed better with three components than with two. Models required the inclusion of a probability mass at full health but results were equivocal between models, with no further probability masses versus those with truncation included at the gap after full health and a probability mass. Whereas AIC/BIC favoured the former, other measures of fit, including visual inspection of the mean EQ-5D-3L by AVVS, favoured the latter. The analyses using the ALDVMM approach also showed that three-component specifications outperformed those with two components, irrespective of other aspects of the specification. Further comparisons were made between ALDVMMs that excluded the modelling of the truncation point below full health and the inclusion of squared AVVS terms both in the component probabilities and as explanatory variables within components. Models with truncation performed universally better than those without truncation. We also found that excluding the squared terms from the component probabilities produced the best-performing models in terms of mean fit, excluding AIC and BIC. However, visual inspection of the plots of mean EQ-5D-3L by AVVS showed that the exclusion of the squared term vastly improved model performance at the lower end of the AVVS, the worst degree of disease severity. Identification of the best model was challenging in part owing to limited data at high disease severity levels. This specification of the ALDVMM had lower MAE than the beta mixture model, excluding RMSE. There is very little to distinguish between the ALDVMM and the beta mixture models, although the ALDVMMs are simpler and more generalisable because they do not need the introduction of ad hoc probability masses at the boundaries.
A very similar pattern of results was found when modelling the post-operative data. Here, four-component models were required to be tested and found to be better performing, for both the beta mixture and the ALDVMM approaches. It was unclear which model type to favour because the results showed that summary fit measures conflicted with each other and there was very little difference across the distribution of AVVS.
Findings
Seven disease areas provided 15 case studies in which mapping methods were applied. The case studies included the EQ-5D-3L (n = 11), EQ-5D-5L (n = 2), SF-6D (n = 1) and HUI3 (n = 1) as dependent variables.
Adding to what is a substantial existing literature, and in line with expectations based on the conflict between the form of utility data and the assumptions inherent in the statistical model, linear regression is shown to perform poorly.
We found that, in all case studies, the more flexible methods for direct utility mapping, which draw on different variants of mixture models with appropriately specified underlying distributions, perform very well. However, the precise form of those models matters.
A minimum of three components are required in mixture models when modelling the EQ-5D-3L, EQ-5D-5L, SF-6D or HUI3. This is in line with our previous experience. In some cases, we found that fitting more than four components was not feasible given the constraints of the data sets available. Nevertheless, good model performance was achieved in all cases.
Typically, the shape of the utility distributions tends to change by case study as a factor of the utility instrument being modelled, the nature of the disease area and the severity of the patient sample. To address this requires the inclusion of covariates that represent disease severity as predictors of the component membership probabilities. The optimal models in all case studies included disease severity both within components and as predictors of component membership.
In most applications, age and gender tend to modify the conditional mean of the classes but are less important in determining the probabilities of component membership.
Spurious clusters are not easy to identify in the left tail of the distribution of the EQ-5D-3L. Often, there is a small number of individuals in very poor health, which might need a separate component distribution. Judgement needs to be exercised in these circumstances as this small component distribution might represent a spurious cluster or a separate component for a small number of individuals. In this case, a component with a small number of individuals is perfectly fine.
The findings clearly demonstrate that there are multiple features of data from utility instruments that need to be reflected in the design and application of appropriate models. It is not simply the case that models need to account for the mass of observations at 1, and the limited nature of the dependent variable. The asthma example in particular shows that, even for the case of the EQ-5D-5L and HUI3, for which the gap is much less pronounced than for the EQ-5D-3L, models that reflect these features perform better than those that do not. We tested this with both different specifications of the beta mixture models and the ALDVMMs (which without the gap at this point become mixtures of tobit-type models).
Finally, simply applying the ALDVMM or beta mixture methods does not in itself provide any protection against misuse nor ensure better fit. These are challenging models to apply and they need to be combined with detailed consideration of the number of components, the inclusion of different truncation points, covariates, their form and whether they appear within the components or in the component probabilities. Good practice needs to be followed in estimation to ensure that the models have genuinely converged. This is a skilled job and, without appropriate application, results can be misleading. Guidance and examples of application of these methods can be found elsewhere. 64,67 The model comparisons we conducted are examinations not only of the performance of broad model types against each other but also of different specifications of these models.
Multidirectional mapping case study
We tested the response mapping model presented in Chapter 3, Indirect methods: systems of ordinal regressions using copulas, in a single case study.
Case study data set: FORWARD
FORWARD, the National Databank for Rheumatic Diseases, is the largest patient-reported research data bank for rheumatic disorders in the USA. It is a register of patients with rheumatoid disease, primarily recruited by referral from US and Canadian rheumatologists. Information supplied by participants is validated by direct reference to records held by hospitals and physicians (a minority of cases come by self-referral, with medical details obtained by FORWARD in the same way). Full details of the recruitment process are given by Wolfe and Michaud. 78 Data are collected by various means, primarily postal and web-based questionnaires completed directly by patients. Data collection began in 1998 and continues to the present, in two waves per annum administered in January and July. In 2011, there was a switch from the EQ-5D-3L to the EQ-5D-5L and both versions were collected simultaneously during the January 2011 wave. The questionnaire includes many general as well as rheumatoid-disease-specific questions. The HAQ disability index is based on patient self-reporting of the degree of difficulty experienced over the previous week in eight categories: dressing and grooming, arising, eating, walking, hygiene, reach, grip and common daily activities. It is widely used by clinicians to measure health outcomes. It is scored in increments of 0.125 between zero and three (although it is standard to consider it fully continuous), with higher scores representing greater degrees of functional disability. The HAQ instrument also includes, separately, a patient self-report of pain scored on a visual analogue scale (0–10). 70 To calculate the expected utilities, the UK and English value sets are used for the EQ-5D-3L and EQ-5D-5L, respectively. 5,6 The study sample size for this case study using only the January 2011 wave was 5192.
Results
The case study used seven covariates: age, gender, the HAQ disability index, the pain scale, and the squares and product of the HAQ and pain scales (i.e. HAQ squared, pain squared and the product of HAQ and pain). A number of different model specifications allowing different number of covariates, mixtures and different copulas for each of the EQ-5D dimensions were tested. The copulas used included Gaussian, Frank, Clayton, Gumbel and Joe copulas (see Chapter 3, Indirect methods: systems of ordinal regressions using copulas) as well as a model of independent EQ-5D dimensions as is conventional in response mapping models.
The selected optimal model according to both AIC and BIC was a joint model with a common mixture for the errors across all 10 equations and different copulas for different dimensions of EQ-5D: Gaussian copulas for mobility and usual activities, Frank copulas for self-care and anxiety/depression and a Gumbel copula for pain/discomfort.
We found that a flexible specification revealed significant differences between individuals’ responses to the EQ-5D-3L and EQ-5D-5L. The differences were particularly large for the mobility and pain dimensions of the EQ-5D, which are the most important dimensions of the EQ-5D for patients with rheumatoid disease. In terms of the utility values, the EQ-5D-5L utility values tended to be systematically higher than the utility values of the EQ-5D-3L so that the distribution function for the EQ-5D-3L was always to the left of the distribution function for the EQ-5D-5L.
To assess the likely impact of these differences together with those introduced by the valuations in an economic evaluation, we used for this case study a trial of combination drug therapies for RA. 96 The original economic evaluation was carried out using the EQ-5D-3L. Using the model to map EQ-5D-3L responses to the EQ-5D-5L, we repeated the economic evaluation in terms of the EQ-5D-5L and found in this case study that the magnitude of the ICERs increased when using the EQ-5D-5L by > 100% in some cases. This result was due to (1) the significant differences to the responses to the mobility and pain dimensions between the two versions of the EQ-5D and (2) the different structures of the valuation systems.
Making the assumption of independence across the EQ-5D dimensions, as is usual in response mapping, or using a restricted set of covariates could also cause a large shift in the ICER.
Full details of the results are reported in Hernández-Alava and Pudney. 70
To check the generalisability of the results, we also estimated different specifications of the same statistical model in another data set. 97 A range of case studies was used to assess the impact of the differences between the EQ-5D-3L and EQ-5D-5L on additional cost-effectiveness studies in different disease areas in the UK.
Findings
This case study highlights, yet again, the importance of taking into account how the model is going to be used to either select from the pool of already available models or develop an appropriate model for the task.
This case study set out to establish the differences between the two versions of the EQ-5D at two levels, the responses to the classification system and the additional differences introduced by the different valuations. Any direct mapping approach will be able to provide only the overall joint effect. Thus, a response mapping approach is needed in this case, but it needs to be flexible enough so that we minimise the risk of imposing restrictions that will bias our results.
A substantial part of the increase in the ICER of the RA case study was due to the different structures of the valuations, suggesting that a similar overall result could be expected in other disease areas. Additional case studies found a similar result: moving from the EQ-5D-3L to EQ-5D-5L decreased the incremental QALYs, increasing the ICER in the majority of cases. The additional case studies also revealed that, for technologies with significant mortality gains, the ICER could change in either direction when moving from the EQ-5D-3L to EQ-5D-5L because improved survival is given a greater value under the EQ-5D-5L owing to the systematic increase in utility values relative to the EQ-5D-3L.
Chapter 5 Additional methodological issues around mapping
The validity of multi-instrument data sets used for mapping: the monotonicity concept
There are several settings in which mapping can be used. The types of statistical models that should be applied are the same, because they are driven by the distributional shape of the dependent variable, but, conceptually, they deal with different issues. The most common type of case involves mapping from a disease-specific measure to a PBM, as in the case studies covered in Chapter 4, Unidirectional case study comparisons. A second type of case maps from one PBM to another: the case study presented in Chapter 4, Multidirectional mapping case study, is an example of this, although mappings between PBMs do not necessarily have to be multidirectional. A third type of case, which is not usually thought of as mapping but is statistically equivalent, involves modelling a PBM conditional on covariates that are not necessarily clinical measures, for example to explore the relationship between the EQ-5D-3L and BMI controlling for other important factors. 98
Mapping is likely to work well only if the set of conditioning variables is able to identify a similar concept to that captured by the PBM. In the third type of case described above, this may be achieved by using a large number of relevant conditioning variables. However, this is often not possible in the first two types of case, in which few covariates are typically available. In the first type of case, mapping from a disease-specific measure to a PBM, it is important that all relevant variables are used in the mapping. Hernández Alava et al. 50 showed that the inclusion of pain (which is part of the HAQ questionnaire but not part of the HAQ disability index summary score) greatly improves models mapping from the HAQ to EQ-5D-3L because pain is an important dimension of the PBM.
In the second type of case, mapping between two PBMs, mapping without additional covariates will work well only if the two outcome measures are closely related in the sense that they are designed to measure the same (or very similar) theoretical concepts. However, this implies that the questionnaire generating the multi-instrument (MI) data set presents the respondent with two sets of very similar questions. This near repetition in an interview may influence response behaviour, leading to systematic differences between the responses that would be given in a MI reference sample and in a conventional single-instrument survey. Such response distortion could lead to bias in the mapping procedure (see Schuman and Presser99 for a survey of the influence of questionnaire context).
Given these concerns, an important first step is to provide empirical evidence on the extent of conflicts between the orderings of health states provided by the two measures. To do that, we introduced the concept of ‘monotonicity’ and corresponding sample estimates of monotonicity rates. This section outlines the approach and gives a flavour of the results for the FORWARD data set, described in Chapter 4, Case study data set: FORWARD, which implements two PBM measures: the EQ-5D-3L and EQ-5D-5L.
Consider the problem of mapping from one health description, X, to an alternative description, Y. X and Y are both vectors, with each element of X or Y describing health in a particular dimension. For example, in our application of mapping the EQ-5D-3L to EQ-5D-5L, X and Y are both five-dimensional vectors, with the dimensions corresponding to mobility, self-care, usual activities, pain, and anxiety/depression. The MI data set contains observed responses for both X (EQ-5D-3L) and Y (EQ-5D-5L) for a sample of n individuals.
We can say that instruments X and Y are perfectly coherent (or technically monotonic) if, when instrument X orders two health states unambiguously in a particular way, the instrument Y always orders them in the same way. For example, if the health of an individual improves between two different time points when the individual completes the EQ-5D-3L but declines according to their EQ-5D-5L responses, then there is a problem of non-monotonicity between the responses of the individual. Because CEA studies use utility values to convert health outcomes into QALYs, if the measurement instruments do not display monotonicity it is impossible to construct equivalent, theoretically valid, utility scales for the two instruments. There would then be cases in which the two measures would generate irreconcilable QALY estimates, giving problems for decision-making based on evidence from the two different measurement instruments. Modest degrees of non-monotonicity should always be expected in applied work because there is likely to be some response ‘noise’ in the data. However, extensive inconsistencies between health state orderings would be a cause for concern, particularly if the inconsistency is concentrated in regions of the distribution of health states that are critical for the outcome of major CEAs.
Ideally, monotonicity would be assessed directly for each individual, using longitudinal data with repeated observations on both instruments, X and Y, for each individual in the MI survey sample. If health state X unambiguously improved (say) from period t to period t + 1, then we would expect instrument Y to show an improvement also. We have been able to find no longitudinal survey containing both the EQ-5D-3L and EQ-5D-5L in multiple waves; however, it is still possible to assess monotonicity indirectly in a cross-section by making comparisons across appropriately selected sample groups.
Choose a specific reference health state, x. Define a subset of the population, S(x), as the set of people who, if interviewed, give a response X = x, and another set, W(x), of people who would report a state worse than x. The population measure, MW(x), of monotonicity relative to the group with worse reported health states is then the probability that a person j selected randomly from set W(x) would report worse health than a person i selected randomly from S(x), using instrument Y, just as the person does using instrument X. Defining the symbol ≺ to mean ‘unambiguously worse in health terms’, the measure MW(x) is written formally as:
Note that there is a natural lower bound for MW(x). In the extreme case where X and Y are independently distributed (which should not be the case if they are conceptually related measures), the event Yj ≺ yi would be independent of Xi and Xj and would occur with a probability of 0.5. Thus, an estimate of MW(x) close to 0.5 would suggest very serious inconsistencies between the two measurement instruments for health states of x and worse.
There are many possible variations on this measure. We can also use a comparison group with better health states than x, rather than worse, leading to a parallel measure:
where the symbol ≻ means ‘unambiguously better in health terms’. MW(x) and MB(x) need not give the same result; for example, if people find it more difficult to give consistent responses when they are describing a currently poor health state, we can expect MW(x) (summarising a comparison between person i in poor health and person j in even poorer health) to give a lower monotonicity rate than MB(x), which compares person i with a person j in better health.
The measures MW(x) and MB(x) are based on only partial orderings of health states, as many pairs of health states cannot be ordered unambiguously (for example, EQ-5D-3L state 22321 is unambiguously better than 33332, but cannot be ordered relative to 23312 without a utility tariff to trade off the pain dimension against the self-care and anxiety/depression dimensions). However, we can also apply the monotonicity analysis to utility values rather than health descriptions, which widens the range of comparisons to cover a full ordering. If the utility scoring systems for instruments X and Y are u(X) and v(Y), then the utility-based version of measure MW(x) is:
where u is a chosen reference utility value. Here, the monotonicity measure is a joint measure of two things: coherence of the underlying survey responses X and Y and of the structures of the utility tariffs u(.) and v(.).
To illustrate this method, we use the FORWARD data set described in Chapter 4, Case study data set: FORWARD, on RA. We summarise the main points here using simple plots of measures M^W(x) and M^B(x) against the EQ-5D-3L utility values u(x), using all reference states x, which are given as responses by at least 25 respondents. As an indication of statistical reliability, we also plot 95% confidence bands, computed using the bootstrap with 200 replications. The results based on direct comparisons of health states X and Y are shown in Figure 9. There are two main conclusions.
FIGURE 9.
Monotonicity measures for health descriptions: FORWARD data. (a) M^W(x); and (b) M^B(x).
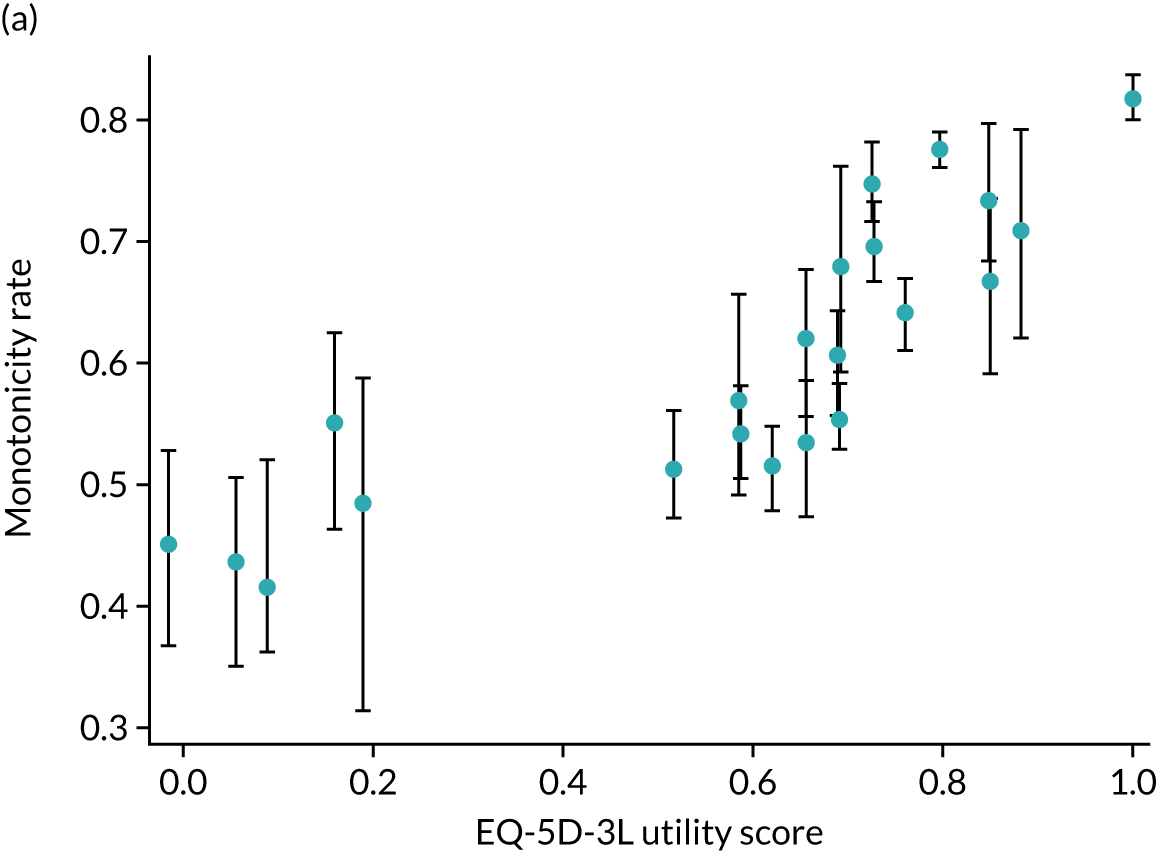
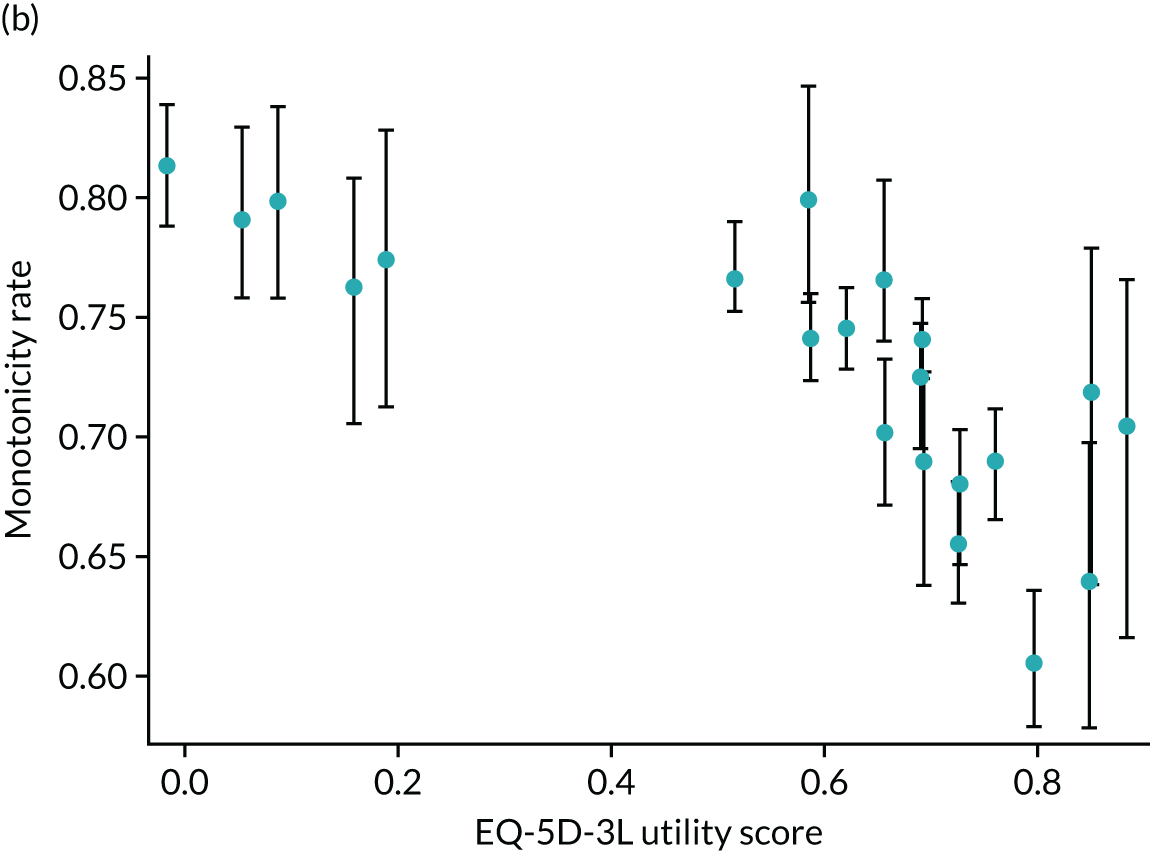
First, in large regions of the health spectrum, monotonicity rates are well below 100% and sometimes close to the 50% rate we would find if X and Y were completely independent.
Second, low monotonicity rates are particularly evident for the measure MW(x) evaluated at low-value health states x with utility value u(x) below about 0.4. Comparisons of poor health states with even poorer states appear to be particularly problematic.
Figure 10 shows estimated monotonicity rates based on utility values rather than health descriptions. Theoretically consistent utility value sets must give exactly the same pairwise ordering in every case where the health descriptions can be unambiguously ordered, because Yj ≻ yi is equivalent to υ(Yj) ≺ υ(yi), etc. However, the ≻ relation gives only a partial ordering, whereas utility values allow us to order every state and thus bring more data points into the estimate at each point.
FIGURE 10.
Monotonicity measures for utility values: FORWARD data. (a) M^W(x); and (b) M^B(x).
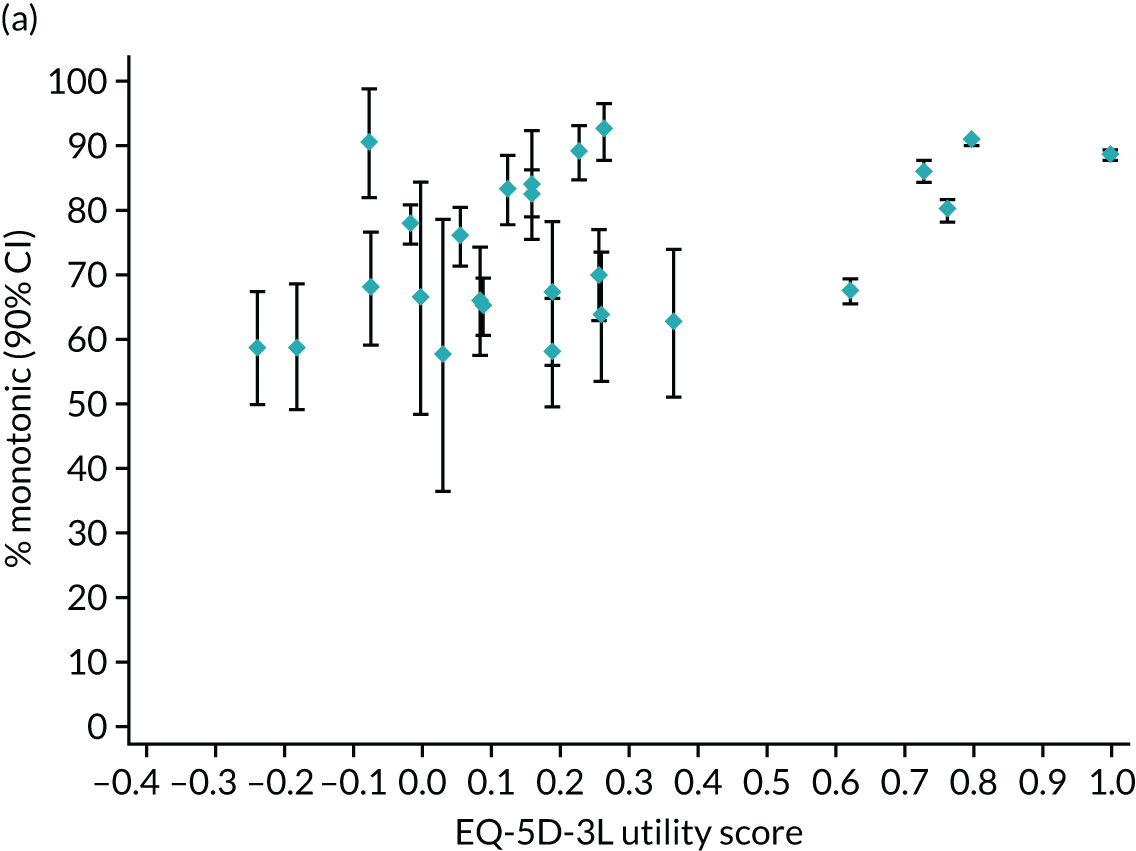
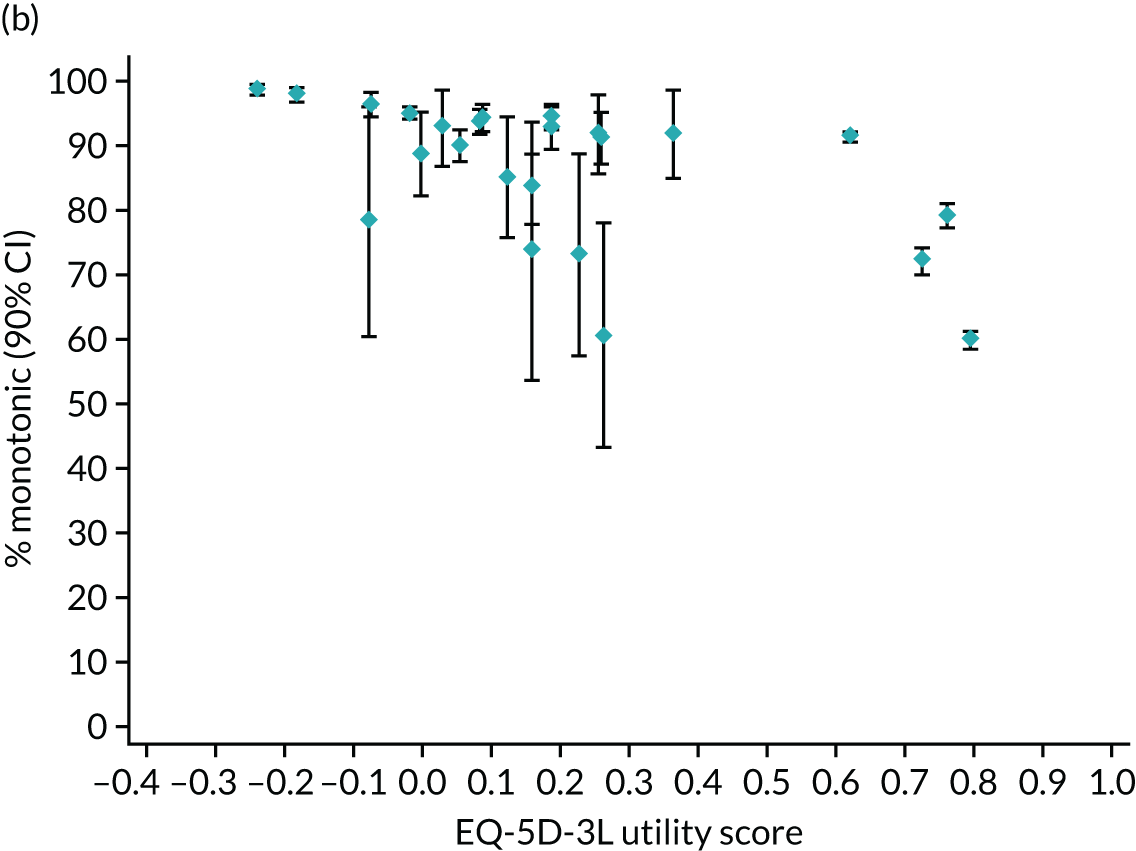
We use the UK value set for the three-level version of the EQ-5D5 and the English value set for the five-level version6 (broadly similar results are found if we work instead with the ‘misery’ index that sums the EQ-5D values across the five dimensions). In most cases, the use of utilities increases monotonicity rates by about 10 percentage points. This increase is likely to be a consequence of the similar way that the two sets of utility values are constructed: both scoring systems build in theoretical valuation axioms and both result from versions of the TTO valuation method.
Overall, the preliminary analysis gives some grounds for concern about the validity of MI reference data sets and the mapping models based on them. There are several alternative interpretations of the low monotonicity rates we have found. It would not be plausible to claim that the inconsistencies we have found between EQ-5D-3L and EQ-5D-5L assessments reflect genuine changes in health-related quality of life over the few minutes separating the EQ-5D-3L and EQ-5D-5L measures in an interview.
Another, perhaps more credible, possibility is that MI surveys, in which respondents receive two sets of similar questions in sequence, are inherently unreliable in the sense that answers to the later version of the EQ-5D instrument are systematically distorted by encountering the other version earlier. There are several reasons, well documented in the survey methods literature, why this might happen: satisficing behaviour by respondents to minimise effort rather than maximising accuracy; failure to appreciate fully that the response scale has changed between the two versions; interview context, because the two versions of the EQ-5D are immediately preceded by other, different, questions, the nature of which might influence response behaviour; or simple annoyance at being asked similar questions twice, resulting in a withdrawal of co-operation.
A second possible source of inconsistency is random measurement error affecting both versions of the instrument. In this case there is no specific unreliability in MI data sets but failures arise through random measurement noise, affecting responses to either version, whether asked alone or in tandem with the other version. The consequences of this type of statistical ‘noise’ may be quite different from the consequences of any behavioural distortions caused by question repetition.
A third possibility is that the two versions of the EQ-5D are interpreted by respondents as asking about different concepts of health-related quality of life. For example, in the mobility domain ‘I am confined to bed’ (EQ-5D-3L) may suggest a qualitatively distinct concept of physical disability and dependency than ‘I am unable to walk about’ (EQ-5D-5L).
Further research is needed to understand the problem better, including research that assesses the extent to which these issues arise for other instruments (both PBMs and non-PBMs) that ask questions that are much less similar than the EQ-5D-3L and EQ-5D-5L. There is also a need to investigate the existence and nature of measurement error. Wider use of test–retest trials in a controlled experimental framework would be informative and could act as a basis for the development of evaluation methods that are more robust to measurement error. The next section, Measurement error, discusses the complex issues raised by measurement error in relation to CEA.
Measurement error
There are potentially two different sources of measurement error in the construction of QALYs for use in an economic evaluation. First, individuals may make mistakes when filling in the responses to the health instrument. It is possible that, at least in part, the high frequency of inconsistencies shown in The validity of multi-instrument data sets used for mapping: the monotonicity concept is due to this unobservable noise. Response error can in principle affect any observation, including those that appear credible, so it is (arguably) preferable to allow for general response error rather than modifying or discarding observations according to some arbitrary consistency rule as in van Hout et al. 100
Second, there may also be error in the utility values. Assuming that true utility values vary randomly across individuals, and that the valuation research (valuation data and subsequent modelling) successfully estimates the mean utilities conditional on any given health state X, then the actual utilities are:
where E(ε) = 0, independently of all other variables. Given the linear dependence of QALY on the utility values, the inability of analysts to estimate the random utility component ε causes no bias. Therefore, in this sense measurement error in the utility value can be ignored; we do this from this point on. Note that misspecification and estimation error in the utility model underlying the form of υ(.) results in systematic functional misspecification rather than measurement error, and we do not address that issue here.
Again, we have two (vector-valued) health state measures, X and Y, provided by different questionnaire instruments, and a set of discrete covariates Z describing the individual and their circumstances. There is a utility value set, u(X) for the instrument X. Consider three hypothetical observational arrangements. The first is a MI reference survey relating to a particular target population described by a distribution f(X,Y,Z). We use the symbol f(.) to refer to any joint conditional or marginal distribution relating to the MI reference population, with the arguments of f indicating the context. The MI reference sample is used to construct a response mapping model that allows us to move between the alternative health description systems X and Y.
The other hypothetical data sources are two clinical trials that are both representative of a target population described by a distribution g(X,Y,Z). The target population is the set of individuals who are believed to be potential beneficiaries of the intervention under trial. A type-1 trial observes only X and Z and, thus, reveals the distribution g(X,Z), whereas a type-2 trial observes only Y and Z and reveals g(Y,Z). The reference population and trial population are not necessarily the same, so f(X,Y,Z) and g(X,Y,Z) are not identical.
Consider a generic and highly simplified CEA focused on the increase in expected QALYs, E6, achieved by some intervention. The body making cost-effectiveness decisions will accept only QALYs based on the utility tariff, υ(.), which has been constructed for the descriptive measure X. However, the decision-making body will also accept values derived from a Y→X mapping applied to data from a type-2 trial that uses the ‘wrong’ health outcome measure. The CEA objective is to determine whether or not the ICER lies within a critical funding threshold or, equivalently, whether or not the expected utility E(u) exceeds a specified policy threshold.
We consider the following five situations:
-
Case 1 – the baseline case where there is no measurement error and the required outcome measure X is directly observed. In this case, there is no bias in the result of the CEA.
-
Case 2 – again there is no measurement error, but the trial observes the ‘wrong’ outcome measure, Y rather than X. Consequently, mapping must be used, via a model estimated from data on X,Y,Z observed in the MI reference sample. In this case there may be bias because the distribution of X|Y,Z in the reference population may not coincide with the distribution of X|Y,Z in the trial population.
-
Case 3 – in this case X is observed directly in the trial so that mapping is unnecessary, but there is random measurement error in the response X, giving the possibility of bias in the estimate of expected utility and thus of the QALY gain.
-
Case 4 – this is a combination of mapping and measurement error: the trial observes Y as its outcome measure rather than X, and there is measurement error in the trial data on Y and in the MI data on X,Y. The measurement error thus affects QALY measurement directly but also indirectly by measurement error bias in the parameters of the econometric mapping model fitted to the reference data set.
-
Case 5 – this is identical to case 4 except that we assume that the investigator has (somehow) succeeded in adjusting the estimated mapping model to remove the measurement error bias in its parameters. However, some bias may remain in the CEA results, from the measurement error in the trial data on Y and mismatch between the reference and trial populations.
To illustrate the way that these biases may work in a practical application, we examine a hypothetical trial based loosely on the structure of an actual evaluation: the CARDERA trial of combination drug therapies for RA. 70,96,101 The original evaluation was carried out using the EQ-5D-3L UK value set. 5 Our analysis assumes that the CEA will be based on the newer EQ-5D-5L instrument using the English value set. 6 There exist no data sets that will allow us to identify and estimate the full statistical structure set, so we use a simulation approach. In simulation studies, it is important to specify the assumed population processes to be as consistent as possible with what we can observe in actual data. This involves calibration: ‘calculation of model parameter values consistent with data, rather than econometric estimation’. 102 In this application, our model parameters are the probability distributions g(X,Y,Z), f(X,Y|Z) and measurement error probabilities. We construct these through a mixture of partial econometric modelling and direct assumption. Here, we sketch the main details and give some preliminary illustrative results.
We use the following assumptions to construct the calibrated model:
-
We use the CARDERA empirical distribution as the assumed target population distribution of a 2-armed trial.
-
We assume that reporting behaviour for the EQ-5D-3L and EQ-5D-5L is uniform across trial arms. This is a critical assumption that, in one form or another, underlies any attempt at evaluation – if we cannot assume that reporting behaviour is invariant to treatment, no reliable comparison between trial arms is possible. We use the empirical distribution of FORWARD (see Chapter 4, Case study data set: FORWARD), which covers patients with RA and matches well the target population of the CARDERA trial to construct the distribution of the EQ-5D-5L conditional on the EQ-5D-3L and covariates. To calculate the true mean QALY in each trial arm, we use a version of the multidirectional mapping model in Chapter 3, Indirect methods: systems of ordinal regressions using copulas, which uses only age and gender as covariates estimated on FORWARD. 70
-
We use the mapping model estimated by van Hout et al. 100 to construct the mapping distribution.
-
The mean discounted incremental cost, E(Δc) = £1500, is based loosely on average costs reported for the CARDERA trial; we assume that expected cost is £6000 in trial arm 1 and £7500 in trial arm 2.
-
We assume a hypothetical measurement error process analogous to the ‘classical’ measurement error assumption. Within each of the five dimensions of the EQ-5D, reporting error distorts measurement symmetrically (except at the limit levels where symmetry is not possible) and independently, by no more than a single position in the hierarchy of health states, and it is independent of the covariates describing the individual and circumstances (see Hernández Alava and Pudney103 for other hypothetical measurement error processes).
Illustrative results of this calibrated model of statistical bias are presented in Table 8. The first row (case 1) gives the true mean QALY difference (0.080) and ICER (£18,780) for the target population chosen via our calibration procedure.
| CEA setting | Arm 1 QALY | Bias in QALY (%) | QALY difference | Bias in QALY difference (%) | ICER (£) | Bias in ICER (%) |
|---|---|---|---|---|---|---|
| Directly observed EQ-5D-5L, no measurement error | 2.6724 | – | 0.0798 | – | 18,781 | – |
| EQ-5D-3L→EQ-5D-5L mapping, no measurement error | 2.6064 | –2 | 0.0964 | 20 | 15,552 | –17 |
| Directly observed EQ-5D-5L, measurement error | 2.6444 | –1 | 0.0803 | 0 | 18,688 | –0 |
| EQ-5D-3L→EQ-5D-5L mapping, measurement error | 1.4660 | –45 | 0.1248 | 56 | 12,015 | –36 |
| EQ-5D-3L→EQ-5D-5L bias-adjusted mapping, measurement error | 2.5769 | –4 | 0.0963 | 21 | 15,582 | –17 |
The second row of Table 8 gives results for case 2 in which the EQ-5D-3L is observed and mapped into the EQ-5D-5L, with no measurement error of any kind. The mismatch between the distribution in the reference population used to construct the mapping function and in the trial target population (based on the FORWARD disease-specific register) generates an upwards bias of 20% in the mean QALY difference, which in turn reduces the measured ICER by 17%. The bias induced by mismatch of the reference sample used for mapping and the trial sample makes the intervention of trial arm 2 appear substantially more cost-effective than it really is. Note that the bias in the difference in QALYs (and therefore also in the ICER) is large, despite the modest bias (–2%) in the QALY levels.
The third row of Table 8 deals with case 3, where the ‘correct’ measure, EQ-5D-5L, is observed, but the health description is subject to small symmetric random reporting errors. The bias in this case is reassuringly small: both QALY levels are understated by about 1%, but their difference, and the implied ICER, are almost unaffected by the reporting error. The small negative bias in QALY estimation is a consequence of ceiling effects for people reporting good health-related quality of life; for example, if the true health state is 11111, then random measurement error can only result in a worse reported state, never a better one.
The last two rows of Table 8 give results for cases 4 and 5 in which the EQ-5D-3L is observed with measurement error and mapped into the EQ-5D-5L (which is also observed with error in the reference sample). The fourth row of Table 8 shows the effect of ignoring the measurement error and the last row gives the results for the case where mapping is assumed to have been corrected for measurement error. Even small degrees of measurement error, as assumed here, lead to large changes in the QALY calculation (–45% in trial arm 1) and even larger changes in the QALY differences between the two trial arms (56%), leading to a reduction in the ICER of 36%. Adjusting the mapping for measurement error reduces the bias in the QALY calculation but still leaves a large downwards bias in the ICER of 17%. This is due to the combined effect of the mismatch between the trial target population and the mapping population and the reporting error in the trial itself.
We found that the distributional mismatch between the trial target population and the mapping population is the main potential source of bias for any CEA involving mapping. We are not aware of any research in this area but our preliminary results show that it can have serious consequences. Measurement error in health responses is a source of bias regardless of whether mapping is used or not. In our simple example, mapping increases the size of the bias but, in principle, mapping may make things better or worse, since there might be offsetting biases. If it were possible to correct for measurement error in estimating the mapping model, the biases would change. In our illustrative example, adjusting for the measurement error in the mapping model reduces the bias but, in general, adjusting for measurement error in mapping may reduce or increase the bias and may make the results more or less comparable with results from trials requiring no mapping. Measurement error in the health description is not only a problem that affects mapping models; it also distorts straightforward evaluations that require no mapping operations. This raises the question of consistency across mapped and direct studies, and even the possibility that ‘correcting’ the mapping model for measurement error, as proposed by Lu et al. ,103 may make even the mapped and direct evaluations less, rather than more, comparable. Moreover, there is no generally accepted set of assumptions about the nature of measurement error, nor any corresponding robust method of correcting mapping models for measurement error bias.
We have presented here some illustrative examples of the type and size of the effects we are likely to see, based on a calibrated model. More research is needed into every aspect of this issue, which is of critical importance for practical policy analysis.
Chapter 6 Discussion and conclusions
This report sets out new findings in the field of mapping. Developments in several areas are documented and tested in case studies.
One of the key shortcomings in the application of mapping models in existing literature has been the poor performance of commonly applied statistical models. Despite the fact that such models systematically mispredict, in some circumstances potentially giving a false picture of the real health benefits of treatments (see Chapter 2, Direct methods), and that there now exists a large amount of supporting empirical evidence, the application of these methods continues. This has led to widespread mistrust of mapping in general.
For mapping to be a reliable approach for bridging the gap between the utility-based estimates required for cost-effectiveness analyses and the type of evidence often generated by clinical studies, it requires statistical methods that yield unbiased results. There is nothing inherently different between this and other regression-based inputs to cost-effectiveness models, though some authors claim otherwise. 104 The requirement for new methods owes much to the challenging nature of the distribution of health utility data. These challenges are present across disease areas and the different generic PBMs used to generate health state utilities. They require flexibility in the statistical modelling methods and a degree of adaptation of methods to suit the peculiarities of the various PBMs.
We demonstrated the inherent limitations associated with the application of linear regression in Chapter 3, Development of methods for mapping. We used data from a large sample, a case study of patients with RA, to estimate models and develop graphical methods for illustrating model performance across the spectrum of disease severity. Plots of the predicted means versus data group means and of the distribution of the data versus the distribution derived from the estimated model are very useful to aid understanding of differences between models, and the potential impact of those differences when translated into economic evaluation. When estimating a mapping model, the analyst should consider if the model might be misspecified. We would encourage any analyst to consider if the assumptions are reasonable and these graphical displays can help with this issue.
Some progress towards developing suitable mapping models is evident in existing literature. In particular, the use of bespoke distributions used in a mixture modelling framework has previously been shown to perform well when mapping to the EQ-5D-3L. 51 The primary aim of the research reported here is to develop this and other methods further, and to test their performance in a series of case studies that use a variety of disease areas and target PBMs.
In particular, we have focused on three classes of methods in addressing this aim: the ALDVMM bespoke mixture model, beta-regression-based methods and developments of multidimensional response mapping. Chapter 3, Development of methods for mapping, describes these developments, their rationale and a variety of options to consider in the application of each broad class of model.
We then used seven case studies to apply and further study these methods. These case studies provided 15 different data sets in which mapping models were estimated using different approaches. The data included the four most commonly applied generic preference-based instruments (EQ-5D-3L, n = 11; EQ-5D-5L, n = 2; SF-6D, n = 1; and HUI3, n = 1) and covered a broad range of diseases including cancers, asthma, heart disease and head injury. The data were collected from randomised clinical trials, disease registries, bespoke patient survey studies and the UK NHS PROMs programme.
The following main findings have implications for mapping practice and potential future research:
-
The evidence shows that linear regression is not an appropriate method for mapping. This is illustrated in Chapter 3, Predictions: mean versus distribution, with a sample of data from the FORWARD database, in which we demonstrate how model performance can be assessed. This is further illustrated in three case study applications in Chapter 4, Unidirectional case study comparisons. Linear regression always performs poorly and is universally worse than models estimated using the other direct methods we examined. This finding is in line with previous studies.
-
Findings from this research show that mixture-based models are capable of providing very accurate results irrespective of the target PBM. However, they need to be applied with considerable attention given to the specific situation. These are more sophisticated models than many analysts will be familiar with; they require a greater degree of statistical experience and judgement on the part of the analyst than for simpler models to ensure that they are estimated appropriately and provide reliable results.
-
We developed freely available software commands to enable the application of mixture-based methods. These commands, available for Stata, cover ALDVMMs 67 and mixture models using the beta distribution . 64
-
Several features of the EQ-5D-3L informed the development of the mixture-based models. These are less prominent in other PBMs, particularly the size of the gap between full health and the next feasible health state, and the multiple modes lower down the distribution. Yet, for all applications, we found that the inclusion of these features remains important for model performance, whether using the ALDVMM or beta mixture models.
-
Optimal mixture models tend to require between three and four components. This may have implications for the size of data sets required for mapping studies. The smallest case study used in this investigation provided 852 observations (for the AQLQ-S asthma study) in which four component ALDVMM and beta-based mixture models were estimated.
-
We also find that there is a requirement for measures of disease severity to be incorporated into predictions of the component probabilities as well as within the components themselves. In many cases, the optimal specification also included age in the component probabilities.
-
Optimal beta-based mixtures and ALDVMMs perform extremely well in the case studies owing to their flexibility. It is not possible to draw universally applicable guidance between these two broad types of models. Beta-based mixtures tend to require at least some probability masses but these are the result of practical considerations rather than theoretical, require additional parameters to be estimated and represent an increase in the number of models that need to be considered. In our applications we found that the relative simplicity of ALDVMMs gave a better fit to the data in general.
-
Response mapping could not always be performed because it relies on sufficient observations for each level within the PBM descriptive system. For PBMs that are based on more complex descriptive systems, for example with increases in the number of response levels, so the likelihood of observing data in all levels diminishes. The case study in people with asthma demonstrates this for both the EQ-5D-5L and HUI3.
-
In those unidirectional case studies in which response mapping methods were applied, we found that the direct methods were better performing.
It is important to note that these case studies address the issue most commonly encountered in mapping, where the requirement is to predict a generic, preference-based outcome utility value from some non-preference-based outcome. Less common, but of substantial importance in allowing decision-makers to assess health technologies using the same outcome measure, is the issue of mapping from one PBM to another. Unlike the traditional mapping case, here our interest is in the ability of the statistical model to allow predictions to be made in either direction. We developed methods and demonstrated their performance (see Chapter 3, Indirect methods: systems of ordinal regressions using copulas, and Chapter 4, Multidirectional mapping case study), using a case study to map between the EQ-5D-3L and EQ-5D-5L. These methods embody several important features for this type of mapping and provide a powerful modelling technique:
-
The approach is designed for mapping between the EQ-5D-3L and EQ-5D-5L, in either direction, in a mutually consistent way.
-
It does not make any assumptions about the two instruments but instead allows the data to determine what is necessary. In particular, it avoids the assumption that the EQ-5D-5L response scale is simply a more detailed categorisation of the same concept in the EQ-5D-3L scale.
-
Covariates are included with no assumption that they influence EQ-5D-3L and EQ-5D-5L responses in the same way.
-
Copulas are used to specify the bivariate distribution of each EQ-5D-3L–EQ-5D-5L pair of responses. This is a way of capturing the associations between EQ-5D-3L and EQ-5D-5L responses, but again in a flexible manner that does not require the assumption that the strength of the association is the same in all parts of the health distribution.
-
A random latent factor allows dependence across the five domains of the EQ-5D, reflecting common underlying causes and individual-specific response styles.
The Stata command 72 was developed to allow analysts to estimate a simplified version of the model of the five bivariate ordinal regressions for each dimension separately. The command allows mapping between the EQ-5D-3L and EQ-5D-5L based on estimated bidirectional mapping models. 71
The development of this approach also provides several potential features that may improve response mapping, which generally did not perform well in the unidirectional case studies reported here. Response mapping approaches do offer the potential advantage of being closely aligned to the data-generating process for utility values from PBMs, and they have practical advantages in allowing different tariffs for different countries to be applied.
Summary of research recommendations
In the process of developing flexible models for mapping, we have uncovered some important issues. The research presented here provides a basis for developing and understanding these issues further. We summarise our research recommendations in what we see as their order of priority in this section.
Typically, it is recommended that some qualitative-type assessment is undertaken of the degree of conceptual overlap between instruments before undertaking a mapping study. 32 We have gone further and examined the extent of conflicts between the orderings of health states in a case study of the EQ-5D-3L and EQ-5D-5L using the concept of monotonicity. Further research is needed to gain a better understanding of the problem. Furthermore, future research should examine the use of monotonicity measures for informing mapping studies that rely on other measures less similar than those in our case study.
We found that distributional mismatch between the trial target population and the population used for mapping is a potential source of bias for CEAs that use mapping. More research is required to understand the likely size of the biases due to distributional mismatch.
We have shown that there are many sources of measurement error in the outcomes used in mapping studies. Some of these are present, and to differing degrees, in the responses being analysed as part of the mapping process. Some are also present when those same measures are used in clinical studies to assess the effectiveness of health technologies, or in clinical practice when assessing patient response. Given this, future research is needed to generate evidence of how and when to adjust for measurement error in mapping.
It is sometimes not feasible to undertake response mapping because of the small numbers of observations in some response categories. This is an issue that may become more prevalent as PBMs introduce more response levels to their descriptive systems. Furthermore, methods often did not perform well compared with direct methods in this study. Nevertheless, response mapping methods maintain a degree of appeal because they are closely related to the data-generating process of PBMs and offer an easier means of generating results that can be used internationally. The development of response mapping methods that harness a greater degree of flexibility remains an area for future research.
Although we have demonstrated the clear benefits of flexible mapping methods, it is sometimes the case that mapping studies are undertaken in very small data sets. This may be because no larger studies have been conducted and, in some disease areas, may not be feasible, for example where patient numbers are very small. It is not clear what should be done in this setting. Future research should investigate options that may include some type of bias adjustment process to be applied to simple methods and single component models (such as the underlying distribution of the ALDVMM). It may be the case that mapping with very limited data is simply best avoided.
Those who design clinical research studies should be aware of the need to collect data that service the needs of economic evaluation. The inclusion of relevant PBMs in all types of clinical studies should be more widespread. In many situations, the inclusion of a PBM in the key clinical trials would obviate the need for mapping. However, the value of data from PBMs applied in large-scale disease registries and other observational studies is obvious from the work reported here. The value generated from the work of large-scale studies such as FORWARD, the National Databank for Rheumatic Diseases, should serve as an exemplar to other disease areas. The collection of these data does not need to be designed with a specific current research question in mind. The decision to include both the EQ-5D-3L and EQ-5D-5L simultaneously in one wave of FORWARD has yielded huge value far beyond decisions relating to the assessment of health technologies for patients with rheumatic disease.
Acknowledgements
We would like to acknowledge the contribution of Joanne Holden of NICE for providing useful input to the design and conduct of this project. We are extremely grateful to those who provided access to data for this project. In particular, we thank Kaleb Michaud from FORWARD, the National Databank for Rheumatic Diseases, Jeff Richardson from the MIC project, Joshua Ray from F. Hoffmann-La Roche AG (Basel, Switzerland), Pharmaceuticals Division, and the staff at the hospitals participating in the VSTR. We wish to acknowledge the use of the CARDERA study data, with thanks to Professor David Scott. We would also like to thank three anonymous referees whose helpful comments have greatly improved this report.
Contributions of authors
Mónica Hernández Alava (https://orcid.org/0000-0003-4474-5883) (Reader in Health Econometrics) conceived, designed and conducted analyses, coded Stata commands and prepared results for publication.
Allan Wailoo (https://orcid.org/0000-0002-9324-1617) (Professor of Health Economics) conceived, designed and conducted analysis and prepared results for publication.
Stephen Pudney (https://orcid.org/0000-0002-5697-0976) (Professor of Econometrics) conceived, designed and conducted analyses, coded Stata commands and prepared results for publication.
Laura Gray (https://orcid.org/0000-0001-6365-7710) (Research Fellow) conducted analyses, contributed to coding the Stata command and prepared results for publication.
Andrea Manca (https://orcid.org/0000-0001-8342-8421) (Professor of Health Economics) contributed to the design of the study, helped revise the report and approved the final version.
Publications
Hernández-Alava M, Wailoo A. Fitting adjusted limited dependent variable mixture models to EQ-5D. Stata J 2015;15:737–50.
Hernández-Alava M, Pudney S. Bicop: a command for fitting bivariate ordinal regressions with residual dependence characterized by a copula function and normal mixture marginals. Stata J 2016;16:159–84.
Hernández-Alava M, Pudney S. Econometric modelling of multiple self-reports of health states: the switch from EQ-5D-3L to EQ-5D-5L, in evaluating drug therapies for rheumatoid arthritis. J Health Econ 2017;55:139–52.
Hernández-Alava M, Wailoo A, Pudney S. Methods for mapping between the EQ-5D-5L and the 3L for technology appraisal. Sheffield: Decision Support Unit, School of Health and Related Research, University of Sheffield; 2017.
Wailoo AJ, Hernández-Alava M, Manca A, Mejia A, Ray J, Crawford B, et al. Mapping to estimate health-state utility from non-preference-based outcome measures: an ISPOR Good Practices for Outcomes Research Task Force Report. Value Health 2017;20:18–27.
Ward Fuller G, Hernández M, Pallot D, Lecky F, Stevenson M, Gabbe B. Health state preference weights for the Glasgow Outcome Scale following traumatic brain injury: a systematic review and mapping study. Value Health 2017;20:141–51.
Gray LA, Hernández Alava M. A command for fitting mixture regression models for bounded dependent variables using the beta distribution. Stata J 2018;18:51–75.
Gray LA, Hernández Alava M, Wailoo A. Development of methods for the mapping of utilities using mixture models: mapping the AQLQ-S to the EQ-5D-5L and the HUI3 in patients with asthma. Value Health 2018;21:748–57.
Gray LA, Wailoo AJ, Hernández Alava M. Mapping the FACT-B instrument to EQ-5D-3L in patients with breast cancer using adjusted limited dependent variable mixture models versus response mapping. Value Health 2018;21:1399–1405.
Hernández-Alava M, Pudney S. EQ5DMAP: a command for mapping between EQ-5D-3L and EQ-5D-5L. Stata J 2018;18:395–415.
Hernández-Alava M, Wailoo A, Grimm S, Pudney S, Gomes M, Sadique Z, et al. EQ-5D-5L versus EQ-5D-3L: the impact on cost effectiveness in the United Kingdom. Value Health 2018;21:49–56.
Data-sharing statement
This is a statistical methods development study and no new data have been generated. All queries should be submitted to the corresponding author.
Patient data
This work uses data provided by patients and collected by the NHS as part of their care and support. Using patient data is vital to improve health and care for everyone. There is huge potential to make better use of information from people’s patient records, to understand more about disease, develop new treatments, monitor safety, and plan NHS services. Patient data should be kept safe and secure, to protect everyone’s privacy, and it’s important that there are safeguards to make sure that it is stored and used responsibly. Everyone should be able to find out about how patient data are used. #datasaveslives You can find out more about the background to this citation here: https://understandingpatientdata.org.uk/data-citation.
Disclaimers
This report presents independent research funded by the National Institute for Health Research (NIHR). The views and opinions expressed by authors in this publication are those of the authors and do not necessarily reflect those of the NHS, the NIHR, NETSCC, the HTA programme or the Department of Health and Social Care. If there are verbatim quotations included in this publication the views and opinions expressed by the interviewees are those of the interviewees and do not necessarily reflect those of the authors, those of the NHS, the NIHR, NETSCC, the HTA programme or the Department of Health and Social Care.
References
- EuroQol Group . EuroQol – a new facility for the measurement of health-related quality of life. Health Policy 1990;16:199-208. https://doi.org/10.1016/0168-8510(90)90421-9.
- Brazier J, Roberts J, Deverill M. The estimation of a preference-based single index measure for health from the SF-36. J Health Economics 2002;21:271-92. https://doi.org/10.1016/S0167-6296(01)00130-8.
- Ware J, Snow K, Kolinski M, Gandeck B. SF-36 Health Survey Manual and Interpretation Guide. Boston, MA: Health Institute, New England Medical Centre; 1993.
- Horseman J, Furlong W, Feeny D, Torrance D. The Health Utilities Index (HUI®): concepts, measurement properties, and applications. Health Qual Life Outcomes 2003;1. https://doi.org/10.1186/1477-7525-1-54.
- Dolan P. Modeling valuations for EuroQol health states. Med Care 1997;35:1095-108. https://doi.org/10.1097/00005650-199711000-00002.
- Devlin NJ, Shah KK, Feng Y, Mulhern B, van Hout B. Valuing health-related quality of life: an EQ-5D-5L value set for England. Health Econ 2018;27:7-22. https://doi.org/10.1002/hec.3564.
- Brazier JE, Rowen D, Hanmer J. Revised SF-6D scoring programmes: a summary of improvements. Patient Reported Outcomes Newsletter 2008;40:14-5.
- Furlong W, Feeny D, Torrance G, Goldsmith C, DePauw S, Zhu Z, et al. Multiplicative Multi-Attribute Utility Function for the Health Utilities Index Mark 3 (HUI3) System: A Technical Report 1998. www.chepa.org/Files/Working%20Papers/WP%2098-11.pdf (accessed 30 October 2019).
- Longworth L, Bryan S. An empirical comparison of EQ-5D and SF-6D in liver transplant patients. Health Econ 2003;12:1061-7. https://doi.org/10.1002/hec.787.
- O’Brien BJ, Spath M, Blackhouse G, Severens JL, Dorian P, Brazier J. A view from the bridge: agreement between the SF-6D utility algorithm and the Health Utilities Index. Health Econ 2003;12:975-81. https://doi.org/10.1002/hec.789.
- Brazier J, Roberts J, Tsuchiya A, Busschbach J. A comparison of the EQ-5D and SF-6D across seven patient groups. Health Econ 2004;13:873-84. https://doi.org/10.1002/hec.866.
- Barton GR, Bankart J, Davis AC, Summerfield QA. Comparing utility scores before and after hearing-aid provision: results according to the EQ-5D, HUI3 and SF-6D. Appl Health Econ Health Policy 2004;3:103-5. https://doi.org/10.2165/00148365-200403020-00006.
- Hernández Alava M, Brazier J, Rowen D, Tsuchiya A. Common scale valuations across different preference-based measures: estimation using rank data. Med Decis Making 2013;33:839-52. https://doi.org/10.1177/0272989X13475716.
- Chen G, Khan MA, Iezzi A, Ratcliffe J, Richardson J. Mapping between 6 multiattribute utility instruments. Med Decis Making 2016;36:160-75. https://doi.org/10.1177/0272989X15578127.
- National Institute for Health and Care Excellence . Guide to the Methods of Technology Appraisal 2013. Process and Methods [PMG9] 2013. www.nice.org.uk/process/pmg9/chapter/foreword (accessed 10 March 2018).
- López-Bastida J, Oliva J, Antoñanzas F, García-Altés A, Gisbert R, Mar J, et al. Spanish recommendations on economic evaluation of health technologies. Eur J Health Econ 2010;11:513-20. https://doi.org/10.1007/s10198-010-0244-4.
- Haute Autorité de Santé . Choices in Methods for Economic Evaluation 2012. www.has-sante.fr/portail/upload/docs/application/pdf/2012-10/choices_in_methods_for_economic_evaluation.pdf (accessed 14 March 2018).
- Teerawattananon Y, Chaikledkaew U. Thai health technology assessment guideline development. J Med Assoc Thail 2008;91:S11-15. https://tools.ispor.org/PEguidelines/source/Thailand-Health-Technology-Assessment-Guidelines.pdf (accessed 25 April 2019).
- Pharmaceutical Benefits Board . Preparing a Health Economic Evaluation to Be Attached to the Application for Reimbursement Status and Wholesale Price for a Medicinal Product: Application Instructions 2017.
- Pharmaceutical Benefits Board . General Guidelines for Economic Evaluations from the Pharmaceutical Benefits Board 2017.
- Agency for Health Technology Assessment . Assessment. Guidelines for Conducting Health Technology Assessment (HTA) 2009.
- Pharmaceutical Management Agency (PHARMAC) . Prescription for Pharmacoeconomic Analysis 2015.
- CADTH . Guidelines for the Economic Evaluation of Health Technologies: Canada 2017.
- Moreno Viscaya M, Mejía A, Castro Jaramillo HE. Manual para la Elaboración de Evaluaciones Económicas en Salud. Bogotá: Institute of Health Technology Assessment; 2014.
- Nederland Z. Guideline for the Conduct of Economic Evaluations in Health Care. Diemen: National Health Care Institute (ZIN); 2016.
- International Society for Pharmacoeconomics and Outcomes Research (ISPOR) . Pharmacoeconomic Guidelines Around the World n.d. https://tools.ispor.org/peguidelines/ (accessed 8 June 2020).
- Mortimer D, Segal L, Sturm J. Can we derive an ‘exchange rate’ between descriptive and preference-based outcome measures for stroke? Results from the transfer to utility (TTU) technique. Health Qual Life Outcomes 2009;7. https://doi.org/10.1186/1477-7525-7-33.
- scharrheds.blogspot.com . Why Does My Mapping Not Predict Health Utilities at 1? 2019. http://scharrheds.blogspot.com/2019/01/why-does-my-mapping-not-predict-health.html (accessed 8 June 2020).
- Dakin H, Abel L, Burns R, Yang Y. Review and critical appraisal of studies mapping from quality of life or clinical measures to EQ-5D: an online database and application of the MAPS statement. Health Qual Life Outcomes 2018;16. https://doi.org/10.1186/s12955-018-0857-3.
- Kearns B, Ara R, Wailoo A, Manca A, Alava MH, Abrams K, et al. Good practice guidelines for the use of statistical regression models in economic evaluations. PharmacoEconomics 2013;31:643-52. https://doi.org/10.1007/s40273-013-0069-y.
- Longworth L, Rowen D. Mapping to obtain EQ-5D utility values for use in NICE health technology assessments. Value Health 2013;16:202-10. https://doi.org/10.1016/j.jval.2012.10.010.
- Wailoo AJ, Hernández-Alava M, Manca A, Mejia A, Ray J, Crawford B, et al. Mapping to estimate health-state utility from non-preference-based outcome measures: an ISPOR Good Practices for Outcomes Research Task Force Report. Value Health 2017;20:18-27. https://doi.org/10.1016/j.jval.2016.11.006.
- Petrou S, Rivero-Arias O, Dakin H, Longworth L, Oppe M, Froud R, et al. The MAPS reporting statement for studies mapping onto generic preference-based outcome measures: explanation and elaboration. PharmacoEconomics 2015;33:993-1011. https://doi.org/10.1007/s40273-015-0312-9.
- Briggs A, Nixon R, Dixon S, Thompson S. Parametric modelling of cost data: some simulation evidence. Health Econ 2005;14:421-8. https://doi.org/10.1002/hec.941.
- Mihaylova B, Briggs A, O’Hagan A, Thompson SG. Review of statistical methods for analysing healthcare resources and costs. Health Econ 2011;20:897-916. https://doi.org/10.1002/hec.1653.
- Khan KA, Petrou S, Rivero-Arias O, Walters SJ, Boyle SE. Mapping EQ-5D utility scores from the PedsQL™ generic core scales. PharmacoEconomics 2014;32:693-706. https://doi.org/10.1007/s40273-014-0153-y.
- Gray LA, Hernández Alava M, Wailoo AJ. Development of methods for the mapping of utilities using mixture models: mapping the AQLQ-S to the EQ-5D-5L and the HUI3 in patients with asthma. Value Health 2018;21:748-57. https://doi.org/10.1016/j.jval.2017.09.017.
- Hurst NP, Kind P, Ruta D, Hunter M, Stubbings A. Measuring health-related quality of life in rheumatoid arthritis: validity, responsiveness and reliability of EuroQol (EQ-5D). Br J Rheumatol 1997;36:551-9. https://doi.org/10.1093/rheumatology/36.5.551.
- Yohai JV. High breakdown-point and high efficiency robust estimates for regression. Ann Stat 1987;17:1662-83. https://doi.org/10.1214/aos/1176350366.
- Mukuria C, Rowen D, Harnan S, Rawdin A, Wong R, Ara R, et al. An updated systematic review of studies mapping (or cross-walking) measures of health-related quality of life to generic preference-based measures to generate utility values. Appl Health Econ Health Policy 2019;17:295-313. https://doi.org/10.1007/s40258-019-00467-6.
- Pennington B, Davis S. Mapping from the Health Assessment Questionnaire to the EQ-5D: the impact of different algorithms on cost-effectiveness results. Value Health 2014;17:762-71. https://doi.org/10.1016/j.jval.2014.11.002.
- Pullenayegum EM, Tarride JE, Xie F, Goeree R, Gerstein HC, O’Reilly D. Analysis of health utility data when some subjects attain the upper bound of 1: are Tobit and CLAD models appropriate?. Value Health 2010;13:487-94. https://doi.org/10.1111/j.1524-4733.2010.00695.x.
- Tobin J. Estimation of relationships for limited dependent variables. Econometrica 1958;26:24-36. https://doi.org/10.2307/1907382.
- Yang F, Devlin N, Luo N. Cost-utility analysis using EQ-5D-5L data: does how the utilities are derived matter?. Value Health 2019;22:45-9. https://doi.org/10.1016/j.jval.2018.05.008.
- Austin P, Escobar M. The use of finite mixture models to estimate the distribution of the Health Utilities Index in the presence of a ceiling effect. J Applied Stat 2003;30:909-23. https://doi.org/10.1080/0266476032000075985.
- Khan KA, Madan J, Petrou S, Lamb SE. Mapping between the Roland Morris Questionnaire and generic preference-based measures. Value Health 2014;17:686-95. https://doi.org/10.1016/j.jval.2014.07.001.
- Kent S, Gray A, Schlackow I, Jenkinson C, McIntosh E. Mapping from the Parkinson’s Disease Questionnaire PDQ-39 to the Generic EuroQol EQ-5D-3L: the value of mixture models. Med Decis Making 2015;35:902-11. https://doi.org/10.1177/0272989X15584921.
- Joyce VR, Sun H, Barnett PG, Bansback N, Griffin SC, Bayoumi AM, et al. Mapping MOS-HIV to HUI3 and EQ-5D-3L in patients with HIV. MDM Policy Pract 2017;2. https://doi.org/10.1177/2381468317716440.
- Khan I, Morris S, Pashayan N, Matata B, Bashir Z, Maguirre J. Comparing the mapping between EQ-5D-5L, EQ-5D-3L and the EORTC-QLQ-C30 in non-small cell lung cancer patients. Health Qual Life Outcomes 2016;14. https://doi.org/10.1186/s12955-016-0455-1.
- Hernández Alava M, Wailoo AJ, Ara R. Tails from the peak district: adjusted limited dependent variable mixture models of EQ-5D questionnaire health state utility values. Value Health 2012;15:550-61. https://doi.org/10.1016/j.jval.2011.12.014.
- Hernández Alava M, Wailoo A, Wolfe F, Michaud K. A comparison of direct and indirect methods for the estimation of health utilities from clinical outcomes. Med Decis Making 2014;34:919-30. https://doi.org/10.1177/0272989X13500720.
- Wailoo A, Hernández Alava M, Escobar Martinez A. Modelling the relationship between the WOMAC Osteoarthritis Index and EQ-5D. Health Qual Life Outcomes 2014;12. https://doi.org/10.1186/1477-7525-12-37.
- Wailoo A, Hernández M, Philips C, Brophy S, Siebert S. Modeling health state utility values in ankylosing spondylitis: comparisons of direct and indirect methods. Value Health 2015;18:425-31. https://doi.org/10.1016/j.jval.2015.02.016.
- Ward Fuller G, Hernández M, Pallot D, Lecky F, Stevenson M, Gabbe B. Health state preference weights for the Glasgow Outcome Scale following traumatic brain injury: a systematic review and mapping study. Value Health 2017;20:141-51. https://doi.org/10.1016/j.jval.2016.09.2398.
- Basu A, Manca A. Regression estimators for generic health-related quality of life and quality-adjusted life years. Med Decis Making 2012;32:56-69. https://doi.org/10.1177/0272989X11416988.
- Young TA, Mukuria C, Rowen D, Brazier JE, Longworth L. Mapping functions in health-related quality of life: mapping from two cancer-specific health-related quality-of-life instruments to EQ-5D-3L. Med Decis Making 2015;35:912-26. https://doi.org/10.1177/0272989X15587497.
- Kaambwa B, Chen G, Ratcliffe J, Iezzi A, Maxwell A, Richardson J. Mapping between the Sydney Asthma Quality of Life Questionnaire (AQLQ-S) and five Multi-Attribute Utility Instruments (MAUIs). PharmacoEconomics 2017;35:111-24. https://doi.org/10.1007/s40273-016-0446-4.
- Khan I, Morris S. A non-linear beta-binomial regression model for mapping EORTC QLQ-C30 to the EQ-5D-3L in lung cancer patients: a comparison with existing approaches. Health Qual Life Outcomes 2014;12. https://doi.org/10.1186/s12955-014-0163-7.
- Smithson M, Verkuilen J. A better lemon squeezer? Maximum-likelihood regression with beta-distributed dependent variables. Psychol Methods 2006;11:54-71. https://doi.org/10.1037/1082-989X.11.1.54.
- Tsuchiya A, Brazier J, McColl E, Parkin D. Deriving Preference-Based Single Indices From Non-Preference-Based Condition-Specific Instruments: Converting AQLQ into EQ5D Indices. Sheffield: University of Sheffield; 2002.
- Gray AM, Rivero-Arias O, Clarke PM. Estimating the association between SF-12 responses and EQ-5D utility values by response mapping. Med Decis Making 2006;26:18-29. https://doi.org/10.1177/0272989X05284108.
- Hernández Alava M, Wailoo A, Wolfe F, Michaud K. The relationship between EQ-5D, HAQ and pain in patients with rheumatoid arthritis. Rheumatology 2013;52:944-50. https://doi.org/10.1093/rheumatology/kes400.
- Conigliani C, Manca A, Tancredi A. Prediction of patient-reported outcome measures via multivariate ordered probit models?. J R Stat Soc Ser A 2015;178:567-91. https://doi.org/10.1111/rssa.12072.
- Gray LA, Hernández Alava M. BETAMIX: a command for fitting mixture regression models for bounded dependent variables using the beta distribution. Stata J 2018;18:51-75. https://doi.org/10.1177/1536867X1801800105.
- McLachlan G, Peel D. Finite Mixture Models. New York, NY: John Wiley & Sons, Inc; 2000.
- Aitkin M. Contribution to the discussion of paper by S. Richardson and P. J. Green. J R Stat Soc Ser B 1997;59:764-8.
- Hernández Alava M, Wailoo A. Fitting adjusted limited dependent variable mixture models to EQ-5D. Stata J 2015;15:737-50. https://doi.org/10.1177/1536867X1501500307.
- Devlin N, Shah K, Feng Y, Mulhern B, van Hout B. Valuing Health-related Quality of Life: An EQ-5D-5L Value Set for England. London: Office of Health Economics; 2016.
- Zimmer DM, Trivedi PK. Copula modeling: an introduction for practitioners. Foundations and Trends® in Econometrics 2006;1:1-111. https://doi.org/10.1561/0800000005.
- Hernández-Alava M, Pudney S. Econometric modelling of multiple self-reports of health states: the switch from EQ-5D-3L to EQ-5D-5L in evaluating drug therapies for rheumatoid arthritis. J Health Econ 2017;55:139-52. https://doi.org/10.1016/j.jhealeco.2017.06.013.
- Hernández-Alava M, Pudney S. Eq5Dmap: a command for mapping between EQ-5D-3L and EQ-5D-5L. Stata J 2018;18:395-41. https://doi.org/10.1177/1536867X1801800207.
- Hernández-Alava M, Pudney SE. BICOP: a command for estimating bivariate ordinal regressions with residual dependence characterized by a copula function and normal mixture marginal?. Stata J 2016;16:159-84. https://doi.org/10.1177/1536867X1601600114.
- Rivero-Arias O, Ouellet M, Gray A, Wolstenholme J, Rothwell PM, Luengo-Fernandez R. Mapping the modified Rankin Scale (mRS) measurement into the generic EuroQol (EQ-5D) health outcome. Med Decis Making 2010;30:341-54. https://doi.org/10.1177/0272989X09349961.
- Longworth L, Rowen D. NICE DSU Technical Support Document 10: The Use of Mapping Methods to Estimate Health State Utility Values. London: NICE; 2011.
- Fayers PM, Hays RD. Should linking replace regression when mapping from profile-based measures to preference-based measures?. Value Health 2014;17:261-5. https://doi.org/10.1016/j.jval.2013.12.002.
- Brazier JE, Yang Y, Tsuchiya A, Rowen DL. A review of studies mapping (or cross walking) non-preference based measures of health to generic preference-based measures. Eur J Health Econ 2010;11:215-25. https://doi.org/10.1007/s10198-009-0168-z.
- Chuang LH, Whitehead SJ. Mapping for economic evaluation. Br Med Bull 2012;101:1-15. https://doi.org/10.1093/bmb/ldr049.
- Wolfe F, Michaud K. The National Data Bank for rheumatic diseases: a multi-registry rheumatic disease data bank. Rheumatology 2011;50:16-24. https://doi.org/10.1093/rheumatology/keq155.
- Briggs A, Sculpher M, Claxton K. Decision Modelling for Health Economic Evaluation. Oxford: Oxford University Press; 2006.
- Brennan A, Chick SE, Davies R. A taxonomy of model structures for economic evaluation of health technologies. Health Econ 2006;15:1295-310. https://doi.org/10.1002/hec.1148.
- Cameron PA, Finch CF, Gabbe BJ, Collins LJ, Smith KL, McNeil JJ. Developing Australia’s first statewide trauma registry: what are the lessons?. ANZ J Surg 2004;74:424-8. https://doi.org/10.1111/j.1445-1433.2004.03029.x.
- Brady MJ, Cella DF, Mo F, Bonomi AE, Tulsky DS, Lloyd SR, et al. Reliability and validity of the Functional Assessment of Cancer Therapy-Breast quality-of-life instrument. J Clin Oncol 1997;15:974-86. https://doi.org/10.1200/JCO.1997.15.3.974.
- Vrdoljak E, Marschner N, Zielinski C, Gligorov J, Cortes J, Puglisi F, et al. Final results of the TANIA randomised phase III trial of bevacizumab after progression on first-line bevacizumab therapy for HER2-negative locally recurrent/metastatic breast cancer. Ann Oncol 2016;27:2046-52. https://doi.org/10.1093/annonc/mdw316.
- Gray LA, Wailoo AJ, Hernández Alava M. Mapping the FACT-B instrument to EQ-5D-3L in patients with breast cancer using adjusted limited dependent variable mixture models versus response mapping. Value Health 2018;21:1399-405. https://doi.org/10.1016/j.jval.2018.06.006.
- Richardson J, Iezzi A, Khan M, Maxwell A. Cross-National Comparison of Twelve Quality of Life Instruments. MIC Paper 1: Background, Questions, Instruments. Clayton, VIC: Monash University; 2012.
- European Medicines Agency (EMA) . Guideline on the Clinical Investigation of Medicinal Products for the Treatment of Asthma 2015. www.ema.europa.eu/en/documents/scientific-guideline/guideline-clinical-investigation-medicinal-products-treatment-asthma_en.pdf (accessed 30 October 2019).
- Everhart RS, Smyth JM, Santuzzi AM, Fiese BH. Validation of the Asthma Quality of Life Questionnaire with momentary assessments of symptoms and functional limitations in patient daily life. Respir Care 2010;55:427-32.
- Krop IE, Kim SB, González-Martín A, LoRusso PM, Ferrero JM, Smitt M, et al. Trastuzumab emtansine versus treatment of physician’s choice for pretreated HER2-positive advanced breast cancer (TH3RESA): a randomised, open-label, phase 3 trial. Lancet Oncol 2014;15:689-99. https://doi.org/10.1016/S1470-2045(14)70178-0.
- Aaronson NK, Ahmedzai S, Bergman B, Bullinger M, Cull A, Duez NJ, et al. The European Organization for Research and Treatment of Cancer QLQ-C30: a quality-of-life instrument for use in international clinical trials in oncology. J Natl Cancer Inst 1993;82:365-76. https://doi.org/10.1093/jnci/85.5.365.
- Bjordal K, de Graeff A, Fayers PM, Hammerlid E, van Pottelsberghe C, Curran D, et al. A 12 country field study of the EORTC QLQ-C30 (version 3.0) and the head and neck cancer specific module (EORTC QLQ-H & N35) in head and neck patients. EORTC Quality of Life Group. Eur J Cancer 2000;36:1796-807. https://doi.org/10.1016/S0959-8049(00)00186-6.
- Aaronson NK, Ahmedzai S, Bergman B, Bullinger M, Cull A, Duez NJ, et al. The European Organisation for Research and Treatment of Cancer QLQ-C30: a quality-of-life instrument for use in international clinical trials in oncology. J Natl Cancer Inst 1993;85:365-76.
- Dawson J, Fitzpatrick R, Murray D, Carr A. Questionnaire on the perceptions of patients about total knee replacement. J Bone Joint Surg Br 1998;80:63-9. https://doi.org/10.1302/0301-620x.80b1.7859.
- Dawson J, Fitzpatrick R, Carr A, Murray D. Questionnaire on the perceptions of patients about total hip replacement. J Bone Joint Surg Br 1996;78:185-90. https://doi.org/10.1302/0301-620X.78B2.0780185.
- Garratt AM, Macdonald LM, Ruta DA, Russell IT, Buckingham JK, Krukowski ZH. Measurement with varicose veins. Qual Heal Care 1993;2:5-10. https://doi.org/10.1136/qshc.2.1.5.
- Ward A, Abisi S, Braithwaite BD. An online patient completed Aberdeen Varicose Vein Questionnaire can help to guide primary care referrals. Eur J Vasc Endovasc Surg 2013;45:178-82. https://doi.org/10.1016/j.ejvs.2012.11.016.
- Wailoo A, Hernández Alava M, Scott IC, Ibrahim F, Scott DL. Cost-effectiveness of treatment strategies using combination disease-modifying anti-rheumatic drugs and glucocorticoids in early rheumatoid arthritis. Rheumatology 2014;53:1773-7. https://doi.org/10.1093/rheumatology/keu039.
- Heráandez Alava M, Wailoo A, Grimm S, Pudney S, Gomes M, Sadique Z, et al. EQ-5D-5L versus EQ-5D-3L: the impact on cost effectiveness in the United Kingdom. Value Health 2018;21:49-56. https://doi.org/10.1016/j.jval.2017.09.004.
- Ara R, Blake L, Gray L, Hernández M, Crowther M, Dunkley A, et al. What is the clinical effectiveness and cost-effectiveness of using drugs in treating obese patients in primary care? A systematic review. Health Technol Assess 2012;16. https://doi.org/10.3310/hta16050.
- Schuman H, Presser S. Questions and Answers in Attitude Surveys. Thousand Oaks, CA: SAGE Publications Ltd; 1996.
- van Hout B, Janssen MF, Feng YS, Kohlmann T, Busschbach J, Golicki D, et al. Interim scoring for the EQ-5D-5L: mapping the EQ-5D-5L to EQ-5D-3L value sets. Value Health 2012;15:708-15. https://doi.org/10.1016/j.jval.2012.02.008.
- Choy EH, Smith CM, Farewell V, Walker D, Hassell A, Chau L, et al. CARDERA (Combination Anti-Rheumatic Drugs in Early Rheumatoid Arhritis) Trial Group . Factorial randomised controlled trial of glucocorticoids and combination disease modifying drugs in early rheumatoid arthritis. Ann Rheum Dis 2008;67:656-63. https://doi.org/10.1136/ard.2007.076299.
- Dawkins C, Srinivasan T, Whalley J, Heckman J, Leamer E. Handbook of Econometrics. Amsterdam: Elsevier; 2005.
- Lu G, Brazier JE, Ades E. Mapping from disease-specific to generic health-related quality-of-life scales: a common factor model. Value Health 2013;16:177-84. https://doi.org/10.1016/j.jval.2012.07.003.
- Round J, Hawton A. Statistical alchemy: conceptual validity and mapping to generate health state utility values. Pharmacoecon Open 2017;1:233-9. https://doi.org/10.1007/s41669-017-0027-2.
List of abbreviations
- AIC
- Akaike information criterion
- ALDVMM
- adjusted limited dependent variable mixture model
- AQLQ-S
- Sydney Asthma Quality of Life Questionnaire
- AVVS
- Aberdeen Varicose Vein Severity
- BIC
- Bayesian information criterion
- CEA
- cost-effectiveness analysis
- CI
- confidence interval
- EORTC
- European Organisation for Research and Treatment of Cancer
- EQ-5D
- EuroQoL-5 Dimensions
- EQ-5D-3L
- EuroQoL-5 Dimensions, three-level version
- EQ-5D-5L
- EuroQoL-5 Dimensions, five-level version
- FACT-B
- Functional Assessment of Cancer Therapy-Breast
- GOS
- Glasgow Outcome Scale
- HAQ
- Health Assessment Questionnaire
- HER2
- human epidermal growth factor receptor 2
- HERC
- Health Economics Research Centre
- HTA
- health technology assessment
- HUI3
- Health Utility Index Mark 3
- ICER
- incremental cost-effectiveness ratio
- MacNew
- MacNew Heart Disease Health-related Quality of Life
- MAE
- mean absolute error
- ME
- mean error
- MI
- multi-instrument
- MIC
- Multi-Instrument Comparison
- NICE
- National Institute for Health and Care Excellence
- OKS
- Oxford Knee Score
- OLS
- ordinary least squares
- PBM
- preference-based measure
- PROM
- patient-reported outcome measure
- QALY
- quality-adjusted life-year
- QLQ-C30
- Quality of Life Questionnaire-Core 30
- RA
- rheumatoid arthritis
- RMSE
- root mean squared error
- SF-36
- Short Form questionnaire-36 items
- SF-6D
- Short Form questionnaire-6 Dimensions
- SG
- standard gamble
- TBI
- traumatic brain injury
- TTO
- time trade-off
- VSTR
- Victorian State Trauma Registry